
Elliptische Koordinaten
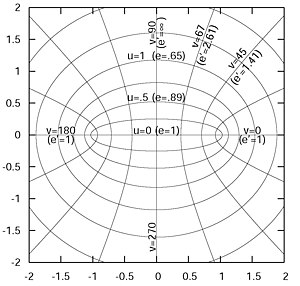
In einem elliptischen Koordinatensystem wird ein Punkt der Ebene durch Angabe der Lage auf konfokalen Ellipsen und Hyperbeln bestimmt. Allgemeiner existieren auch elliptische Koordinatensysteme im dreidimensionalen Raum.
Ebene elliptische Koordinaten
Definition
Üblicherweise wählt man die zwei Brennpunkte an den Stellen
und
auf der
-Achse
eines kartesischen
Koordinatensystems. Der Punkt mit den elliptischen Koordinaten
hat dann die kartesischen Koordinaten
mit
und
.
Fasst man die Ebene als komplexe
Ebene auf, so gilt
Transformationen
Zur Transformation von elliptischen in kartesische Koordinaten
werden ganz einfach die obigen Beziehungen verwendet.
Um die inverse Transformation
durchzuführen muss man die prinzipielle Idee dieser Koordinaten zu Hilfe nehmen.
Diese besagt, dass der Punkt
sowohl auf einer Ellipse als auch auf einer
konfokalen Hyperbel
liegen muss. Diese besitzen Halbachsen wie im unteren Abschnitt angegeben.
Mithilfe der Ellipsen- und Hyperbelgleichung in kartesischen Koordinaten und Hauptachsenform
folgt daraus:
und
.
Diese Gleichungen werden durch die oben angegebenen kartesischen Darstellungen erfüllt.
Hieraus lassen sich unter Verwendung der elementaren Beziehungen der trigonometrischen bzw. hyperbolischen Funktionen
und
folgende Transformationsvorschriften ableiten:
mit der schreibvereinfachenden Substitution .
Weitere Transformationen wie beispielsweise von ebenen Polarkoordinaten auf elliptische Koordinaten lassen sich über den Zwischenschritt der kartesischen Koordinaten durchführen.
Eigenschaften
Die -Koordinatenlinien sind
Hyperbeln,
die
-Koordinatenlinien
Ellipsen.
Für
ist die
-Koordinatenlinie
zur Verbindungsstrecke der beiden Brennpunkte entartet. Für
ist die
-Koordinatenlinie
zur Halbgeraden
auf der
-Achse
entartet, für
zur dazu spiegelsymmetrischen Halbgerade auf der negativen
-Achse.
Für
und
ist die
-Koordinatenlinie
die positive bzw. die negative
-Achse.
Alle Ellipsen und Hyperbeln haben die gleiche lineare
Exzentrizität .
Die Ellipsen, auf denen
konstant ist, haben die große Halbachse
,
die kleine Halbachse
und numerische
Exzentrizität
.
Die Hyperbeln, auf denen
konstant ist, haben die reelle Halbachse
,
die imaginäre Halbachse
und numerische Exzentrizität
.
Die Darstellung in dieser Koordinatenform ist nur deshalb möglich, da Cosinus
hyperbolicus und Sinus hyperbolicus bzw. Cosinus
und Sinus die Beziehungen zwischen großer und kleiner Halbachse ()
bei Ellipsen
bzw. realer und imaginärer Halbachse bei Hyperbeln
(
)
trivial erfüllen.
Verallgemeinerung auf drei Dimensionen
Diese elliptischen Koordinaten können auf verschiedene Arten auf den
dreidimensionalen Raum erweitert werden. Bei zylindrischen elliptischen
Koordinaten wird einfach die kartesische -Koordinate
als weitere Koordinate hinzugefügt. Bei polaren elliptischen Koordinaten wird
die Ebene um einen Winkel
gedreht, der dann die zusätzliche Koordinate bildet:
Schließlich gibt es noch räumlich elliptische Koordinaten:
Hier ist b ein weiterer Parameter des Koordinatensystems. Die -Koordinatenlinien
sind hier Ellipsen. Die Koordinate
läuft hier von 0 bis
,
die Koordinate
von 0 bis unendlich und
von 0 bis
.
Anwendungen
Durch die Transformation auf elliptische Koordinaten kann die Schrödinger-Gleichung für das H2+-Molekül in Born-Oppenheimer-Näherung analytisch gelöst werden.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.07. 2021