Vektorinvariante

Die Vektorinvariante ist eine vektorielle Eigenschaft, die einem Tensor zweiter Stufe zugeordnet werden kann. Die Komponenten eines Tensors referenzieren auf Dyaden von Vektoren, die sich ihrerseits komponentenweise bezüglich einer Vektorraumbasis darstellen lassen. Bei einem Wechsel der Basis ändern sich die Komponenten der Vektoren in charakteristischer Weise nicht aber die Beträge der Vektoren. Der Betrag eines Vektors ist also invariant gegenüber einem Wechsel der Basis. Ebenso ist die Vektorinvariante eines Tensors invariant gegenüber einem Wechsel der Basis. Weil das Kreuzprodukt in die Definition eingeht, ist die Vektorinvariante nur in drei Dimensionen definiert.

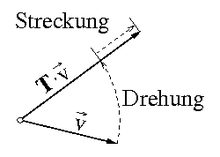
Lineare Abbildung eines Vektors ${\vec {v}}$ durch einen Tensor T.

Tensoren zweiter Stufe werden als lineare Abbildungen von geometrischen Vektoren auf geometrische Vektoren benutzt, die im Allgemeinen dabei gedreht und gestreckt werden, siehe Abbildung rechts. Die Vektorinvariante wird bei der Beschreibung von Drehungen benutzt: Sie ist die Drehachse, um die ein orthogonaler Tensor einen Vektor dreht, und die Winkelgeschwindigkeit ist proportional zur Vektorinvariante des Geschwindigkeitsgradienten.

Definition

Die Vektorinvariante ${\vec {i}}$ einer Dyade ${\vec {a}}\otimes {\vec {b}}$ von Vektoren ${\vec {a}},\,{\vec {b}}\in \mathbb {V}$ aus dem dreidimensionalen euklidischen Vektorraum $\mathbb {V}$ entsteht, indem das dyadische Produkt „ $\otimes$ “ durch das Kreuzprodukt „×“ ersetzt wird:

${\vec {i}}({\vec {a}}\otimes {\vec {b}})={\vec {a}}\times {\vec {b}}\,.$

Wenn der Vektor ${\vec {b}}$ parallel zum Vektor ${\vec {a}}$ ist, dann ist die Dyade symmetrisch und die Vektorinvariante verschwindet. Die Ersetzung des dyadischen Produkts durch das Kreuzprodukt in einer Dyade kann mit dem „Skalarkreuzprodukt“ ^[1] mit dem Einheitstensor 1 erreicht werden:

$\mathbf {1} \cdot \!\!\times ({\vec {a}}\otimes {\vec {b}})=\left(\sum _{i=1}^{3}{\hat {e}}_{i}\otimes {\hat {e}}_{i}\right)\cdot \!\!\times ({\vec {a}}\otimes {\vec {b}}):=\sum _{i=1}^{3}({\hat {e}}_{i}\cdot {\vec {a}}){\hat {e}}_{i}\times {\vec {b}}={\vec {a}}\times {\vec {b}}\,.$

Die Vektoren ${\hat {e}}_{1,2,3}$ stehen hier für eine Orthonormalbasis und „·“ für das im euklidischen Vektorraum definierte Skalarprodukt. Für einen Tensor zweiter Stufe T, der immer als Summe von Dyaden darstellbar ist, bestimmt sich die Vektorinvariante demnach gemäß

$\mathbf {T} _{\times }:={\vec {i}}(\mathbf {T} ):=\mathbf {1\cdot \!\!\times T} \,.$

Die Schreibweise $\mathbf {T} _{\times }$ ist aus Altenbach (2012). Bezüglich der Orthonormalbasis ${\hat {e}}_{1,2,3}$ schreibt sich speziell:

$\mathbf {T} =\sum _{i,j=1}^{3}T_{ij}{\hat {e}}_{i}\otimes {\hat {e}}_{j}\quad \rightarrow \quad {\vec {i}}(\mathbf {T} )={\begin{pmatrix}T_{23}-T_{32}\\T_{31}-T_{13}\\T_{12}-T_{21}\end{pmatrix}}$

Invarianz

Der Nachweis der Invarianz der Vektorinvariante gelingt mit Transformationen der Form

$\mathbf {U} :=\sum _{i=1}^{3}{\vec {u}}_{i}\otimes {\vec {u}}^{i}\,,$

die Einheitstensoren sind und beim Produkt mit einem Tensor den Tensor nicht verändern. Die Vektoren ${\vec {u}}_{{1,2,3}}$ müssen hier eine Vektorraumbasis bilden und ${\vec {u}}^{{1,2,3}}$ sind die dazu duale Basis. Gegeben sei nun ein Tensor zweiter Stufe mit Komponenten $T_{ij}$ bezüglich zweier beliebiger Basissysteme ${\vec {a}}_{1,2,3}$ und ${\vec {b}}_{1,2,3}\,:$

$\mathbf {T} =\sum _{i,j=1}^{3}T_{ij}{\vec {a}}_{i}\otimes {\vec {b}}_{j}\,.$

Mit Transformationen U und V entsteht der Tensor mit Komponenten bezüglich der Basen ${\vec {u}}_{{1,2,3}}$ bzw. ${\vec {v}}_{1,2,3}\,:$

${\begin{aligned}\mathbf {T} =&\mathbf {U\cdot T\cdot V} ^{\top }\\=&\sum _{i,j,k,l=1}^{3}({\vec {u}}_{k}\otimes {\vec {u}}^{k})\cdot (T_{ij}{\vec {a}}_{i}\otimes {\vec {b}}_{j})\cdot ({\vec {v}}^{l}\otimes {\vec {v}}_{l})\\=&\sum _{i,j,k,l=1}^{3}\underbrace {[T_{ij}({\vec {u}}^{k}\cdot {\vec {a}}_{i})({\vec {v}}^{l}\cdot {\vec {b}}_{j})]} _{:=T_{kl}^{*}}{\vec {u}}_{k}\otimes {\vec {v}}_{l}\\=&\sum _{k,l=1}^{3}T_{kl}^{*}{\vec {u}}_{k}\otimes {\vec {v}}_{l}\end{aligned}}$

Das hochgestellte „T“ steht für die Transposition. Damit berechnet sich

${\begin{aligned}{\vec {i}}(\mathbf {U\cdot T\cdot V} ^{\top })=&\sum _{k,l=1}^{3}T_{kl}^{*}{\vec {u}}_{k}\times {\vec {v}}_{l}\\=&\sum _{i,j,k,l=1}^{3}[T_{ij}({\vec {u}}^{k}\cdot {\vec {a}}_{i})({\vec {v}}^{l}\cdot {\vec {b}}_{j})]{\vec {u}}_{k}\times {\vec {v}}_{l}\\=&\sum _{i,j=1}^{3}T_{ij}{\vec {a}}_{i}\times {\vec {b}}_{j}\\=&{\vec {i}}(\mathbf {T} )\,.\end{aligned}}$

Die Vektorinvariante verdient ihren Namen also.

Axialität und Objektivität

Wenn die obigen Transformationen identisch und orthogonal sind, also die Eigenschaft $\mathbf {Q\cdot Q} ^{\top }=\mathbf {1}$ besitzen, dann ergibt sich für einen wie oben vorgegebenen Tensor T:

${\begin{aligned}{\vec {i}}(\mathbf {Q\cdot T\cdot Q} ^{\top })=&{\vec {i}}\left(\mathbf {Q} \cdot \left(\sum _{i,j=1}^{3}T_{ij}{\vec {a}}_{i}\otimes {\vec {b}}_{j}\right)\cdot \mathbf {Q} ^{\top }\right)\\=&{\vec {i}}\left(\sum _{i,j=1}^{3}T_{ij}(\mathbf {Q} \cdot {\vec {a}}_{i})\otimes (\mathbf {Q} \cdot {\vec {b}}_{j})\right)\\=&\sum _{i,j=1}^{3}T_{ij}(\mathbf {Q} \cdot {\vec {a}}_{i})\times (\mathbf {Q} \cdot {\vec {b}}_{j})\\=&\operatorname {det} (\mathbf {Q} )\mathbf {Q} \cdot \sum _{i,j=1}^{3}T_{ij}{\vec {a}}_{i}\times {\vec {b}}_{j}\\=&\operatorname {det} (\mathbf {Q} )\mathbf {Q} \cdot {\vec {i}}(\mathbf {T} )\,.\end{aligned}}$

Wenn Q eigentlich orthogonal ist, dann ist seine Determinante det gleich eins und die Vektorinvariante objektiv, denn sie transformiert sich bei einer euklidischen Transformation wie ein objektiver Vektor.

Bei einer Drehspiegelung um ${\vec {i}}$ gilt $\mathbf {Q} \cdot {\vec {i}}=-{\vec {i}}\,,\;\operatorname {det} \mathbf {Q} =-1$ und daher

${\vec {i}}(\mathbf {Q\cdot T\cdot Q} ^{\top })={\vec {i}}(\mathbf {T} )\,.$

Vektoren mit dieser Eigenschaft bei einer Drehspiegelung sind axiale Vektoren.

Dualer Vektor und Kreuzproduktmatrix

Jedem schiefsymmetrischen Tensor T kann über

$\mathbf {T} \cdot {\vec {v}}={\vec {t}}\times {\vec {v}}\quad {\text{für alle}}\quad {\vec {v}}\in \mathbb {V}$

ein dualer Vektor ${\vec {t}}$ zugeordnet werden. Der duale Vektor ist proportional zur Vektorinvariante:

${\vec {t}}=-{\frac {1}{2}}{\vec {i}}(\mathbf {T} )=-{\frac {1}{2}}\mathbf {1\cdot \!\!\times T} \,.$

Bezüglich der Orthonormalbasis ${\hat {e}}_{1,2,3}$ schreibt sich speziell:

$\mathbf {T} =\sum _{i,j=1}^{3}T_{ij}{\hat {e}}_{i}\otimes {\hat {e}}_{j}\quad \rightarrow \quad {\vec {t}}=-{\frac {1}{2}}\sum _{i,j=1}^{3}T_{ij}{\hat {e}}_{i}\times {\hat {e}}_{j}=\left({\begin{array}{c}T_{32}\\T_{13}\\T_{21}\end{array}}\right)\,.$

Der Tensor T kann mittels $\mathbf {T} ={\vec {t}}\times \mathbf {1}$ aus seinem dualen Vektor rekonstruiert werden. In der linearen Algebra heißt die dem Vektor ${\vec {t}}$ analog zugeordnete Matrix Kreuzproduktmatrix.

Eigenschaften

Mit elementarer Tensoralgebra können die folgenden Eigenschaften der Vektorinvariante nachgewiesen werden. Seien x eine beliebige Zahl, ${\vec {v}}$ ein beliebiger Vektor und $\mathbf {S} ,\,\mathbf {T}$ beliebige Tensoren zweiter Stufe. Dann gilt:

${\begin{aligned}{\vec {i}}(\mathbf {T} ^{\top })=&-{\vec {i}}(\mathbf {T} )\\{\vec {i}}(\mathbf {S+T} )=&{\vec {i}}(\mathbf {S} )+{\vec {i}}(\mathbf {T} )\\{\vec {i}}(x\mathbf {T} )=&x\,{\vec {i}}(\mathbf {T} )\\{\vec {i}}(\mathbf {S} \#\mathbf {T} )=&\mathbf {S} \cdot {\vec {i}}(\mathbf {T} )+\mathbf {T} \cdot {\vec {i}}(\mathbf {S} )\\\mathbf {T} \cdot {\vec {i}}(\mathbf {T} )=&\mathbf {T} ^{\top }\cdot {\vec {i}}(\mathbf {T} )={\vec {i}}(\mathbf {T} )\cdot \mathbf {T} \\{\vec {i}}(\operatorname {cof} (\mathbf {T} ))=&\mathbf {T} \cdot {\vec {i}}(\mathbf {T} )\\{\vec {i}}(\mathbf {T} ^{-1})=&-{\frac {1}{\operatorname {det} (\mathbf {T} )}}\mathbf {T} \cdot {\vec {i}}(\mathbf {T} )\quad {\text{falls}}\quad \operatorname {det} (\mathbf {T} )\neq 0\\{\vec {i}}(\mathbf {T\cdot S\cdot T} ^{\top })=&\operatorname {cof} (\mathbf {T} )\cdot {\vec {i}}(\mathbf {S} )\\{\vec {i}}(\mathbf {T} )\times {\vec {v}}=&(\mathbf {T^{\top }-T} )\cdot {\vec {v}}\\{\vec {i}}({\vec {v}}\times \mathbf {1} )=&-2{\vec {v}}\end{aligned}}$

Darin sind „#“ das äußere Tensorprodukt,

$\operatorname {cof} (\mathbf {T} ):=\mathbf {T} ^{\top }\cdot \mathbf {T} ^{\top }-\operatorname {I} _{1}(\mathbf {T} )\mathbf {T} ^{\top }+\operatorname {I} _{2}(\mathbf {T} )\mathbf {1} ={\frac {1}{2}}\mathbf {T} \#\mathbf {T}$

der Kofaktor und I_1,2 Hauptinvarianten des Tensors T.

Aus den ersten beiden Eigenschaften folgt, dass nur der schiefsymmetrische Anteil eines Tensors zur Vektorinvariante etwas beiträgt und symmetrische Tensoren den Nullvektor als Vektorinvariante besitzen.

Anmerkung

↑ Das Skalarkreuzprodukt ist mit Vektoren ${\vec {a}},\,{\vec {b}},\,{\vec {c}},\,{\vec {d}}\in \mathbb {V}$ definiert über
$({\vec {a}}\otimes {\vec {b}})\cdot \!\!\times ({\vec {c}}\otimes {\vec {d}}):=({\vec {b}}\cdot {\vec {c}}){\vec {a}}\times {\vec {d}}\,.$

Basierend auf einem Artikel in:

Wikipedia.de