Euklidische Transformation

Die euklidische Transformation, benannt nach Euklid, ist eine abstands- und damit auch winkelerhaltende Transformation des euklidischen Raumes auf sich. Bei der eigentlichen euklidischen Transformation bleibt zusätzlich die Orientierung erhalten, werden also Spiegelungen ausgeschlossen.

Mechanisch stellt die eigentliche euklidische Transformation die allgemeine Beobachtertransformation dar und bedeutet eine zeitabhängige Translation und Rotation des Bezugssystems des Beobachters. Nur die eigentlichen Transformationen sind physikalisch, weil Spiegelungen enthaltende Transformationen materieller Körper in der Natur nicht vorkommen. Anschaulich kann man sich die allgemeine Beobachtertransformation als eine Starrkörperbewegung eines Bezugssystems vorstellen, bei der der Ursprung und die angehefteten Koordinatenachsen sich beliebig bewegen, aber die Koordinatenachsen die relative Orientierung und Winkel zueinander beibehalten und nicht gedehnt oder gestaucht werden. Die Galilei-Transformation ist hierin als Spezialfall der geradlinig-gleichförmigen Bewegung enthalten.

Die euklidische Transformation wird zur Definition objektiver oder invarianter Größen benutzt, die von Beobachtern in unterschiedlich bewegten Bezugssystemen in gleicher Weise wahrgenommen werden, siehe Wechsel des Bezugssystems. Objektive Größen, die den Zustand eines materiellen Körpers beschreiben, sind in der Materialtheorie von zentraler Bedeutung, denn es entspricht nicht der Erfahrung, dass ein bewegter Beobachter ein anderes Materialverhalten misst wie ein ruhender. Diese Gesetzmäßigkeit wird materielle Objektivität genannt.

Überblick

Die Darstellung erfolgt in drei Dimensionen, kann aber in einfacher Weise auf n Dimensionen verallgemeinert werden. Die euklidische Transformation ist eine abstandserhaltende Transformation eines euklidischen Raumes auf sich. Da er eine Abstandsfunktion enthält, ist der euklidische Raum ein Metrischer Raum und die euklidische Transformation eine Isometrie. Bezüglich der Hintereinanderausführung bilden die euklidischen Transformationen eine Gruppe.

Je nachdem welche Art Euklidischer Raum zu Grunde gelegt wird, liegen verschiedene Formulierungen vor:

Die Transformation des euklidischen Punktraumes $\mathbb{E}^3$ ist eine Bewegung (Mathematik), die ebenfalls eigentlich genannt wird, wenn die Orientierung erhalten bleibt, und uneigentlich, wenn dies nicht der Fall ist.
Die euklidische Transformation des Koordinatenraumes $\mathbb {R} ^{3}$ mit dem Standardskalarprodukt über dem Körper $\mathbb {R}$ ist eine spezielle Koordinatentransformation, bei der die Transformationsmatrix eine orthogonale Matrix ist (siehe Beschreibung in Koordinaten).
Die Transformation des euklidischen Vektorraumes $\mathbb{V}^3$ (einem über $\mathbb {R}$ definierten Vektorraum mit Skalarprodukt) wird hier in einem physikalischen Zusammenhang dargestellt.

Euklidische Transformation und Beobachterwechsel

Verschiebungen und Vektoren

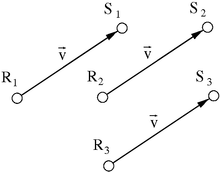
Bei der euklidischen Transformation wird vom euklidischen Punktraum $\mathbb{E}^3$ unserer Anschauung ausgegangen und diesem ein euklidischer Vektorraum $\mathbb{V}^3$ zugeordnet, siehe Vom euklidischen Anschauungsraum zum euklidischen Vektorraum. Zusammenfassend liegt jedem euklidischen Vektorraum eine längentreue Abbildung

${\begin{array}{llll}{\mathcal {V}}:&{\mathbb {E}}^{3}\times {\mathbb {E}}^{3}&\mapsto &{\mathbb {V}}^{3}\\&(R,S)&\mapsto &{\vec {v}}\end{array}}$

zu Grunde, die allen parallelen, gleichsinnigen und gleich langen Verschiebungen von Punkten zu Punkten einen gleichlangen Vektor ${\vec {v}}$ zuordnet, siehe Bild. Die Bedeutung hiervon wird in der aktiven Interpretation des Beobachterwechsels deutlich^[1].

Passive Interpretation oder Koordinatentransformation

Veranschaulichung der Koordinatentransformation

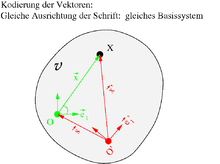
Durch Auswahl von vier nicht in einer Ebene liegenden Punkten $O,P_{{1}},P_{2},P_{3}\in {\mathbb {E}}^{3}$ , von denen den Ursprung darstellt, wird eine Basis ${\mathcal {V}}(O,P_{i})={\vec {e}}_{i}$ des $\mathbb{V}^3$ entworfen. Der Einfachheit halber sollen die Vektoren ${\mathcal {V}}(O,P_{i})={\vec {e}}_{i}$ paarweise senkrecht aufeinander stehen und jeweils die Länge eins haben, so dass die Basisvektoren ${\vec {e}}_{i}$ eine Orthonormalbasis darstellen. Jedem Punkt $X\in {\mathbb {E}}^{3}$ können nun Koordinaten ${x}_{i}\in {\mathbb {R}}$ zugeordnet werden:

${\mathcal {V}}(O,X)=:{\vec {x}}=\sum _{{i=1}}^{3}x_{i}{\vec {e}}_{i}\quad {\textsf {mit\ den\ Komponenten}}\quad x_{i}:={\vec {e}}_{i}\cdot {\vec {x}}\,.$

Ein Wechsel des Bezugssystems wird nun durch Auswahl von vier anderen Punkten $O',P'_{1},P'_{2},P'_{3}\in {\mathbb {E}}^{3}$ bewerkstelligt, was auf die neue Orthonormalbasis ${\vec {e}}'_{i}$ führt, siehe Bild. Der Punkt erhält im neuen Bezugssystem andere Koordinaten x'_i :

${\mathcal {V}}(O',X)=:{\vec {x}}'=\sum _{{i=1}}^{3}x'_{i}{\vec {e}}'_{i}\,.$

Mit

${\mathcal {V}}(O',O)=:{\vec {s}}=\sum _{{i=1}}^{3}s_{i}{\vec {e}}'_{i}$

ergibt sich die Vektorgleichung

${\mathcal {V}}(O',X)={\mathcal {V}}(O',O)+{\mathcal {V}}(O,X)\Leftrightarrow \sum _{{i=1}}^{3}x'_{i}{\vec {e}}'_{i}=\sum _{{i=1}}^{3}s_{i}{\vec {e}}'_{i}+\sum _{{j=1}}^{3}x_{j}{\vec {e}}_{j}=\sum _{{i=1}}^{3}s_{i}{\vec {e}}'_{i}+\sum _{{i,j=1}}^{3}x_{j}({\vec {e}}'_{i}\cdot {\vec {e}}_{j}){\vec {e}}'_{i}\,.$

Den Zusammenhang zwischen den Koordinaten beschreibt die Koordinatentransformation

$x'_{i}=s_{i}+\sum _{{j=1}}^{3}Q_{{ij}}x_{j}\Leftrightarrow \left({\begin{array}{c}x'_{1}\\x'_{2}\\x'_{3}\end{array}}\right)=\left({\begin{array}{c}s_{1}\\s_{2}\\s_{3}\end{array}}\right)+\left({\begin{array}{ccc}Q_{{11}}&Q_{{12}}&Q_{{13}}\\Q_{{21}}&Q_{{22}}&Q_{{23}}\\Q_{{31}}&Q_{{32}}&Q_{{33}}\end{array}}\right)\cdot \left({\begin{array}{c}x_{1}\\x_{2}\\x_{3}\end{array}}\right)\,.$

Dies ist eine Matrizengleichung wie in Beschreibung in Koordinaten oder Isometrien. Die 3 × 3 Matrix mit den Komponenten $Q_{{ij}}={\vec {e}}'_{i}\cdot {\vec {e}}_{j}$ ist eine orthogonale Matrix und daher gilt

$QQ^{\top }=I\,,$

worin die Einheitsmatrix darstellt. Falls für die Determinante ${\mathrm {det}}(Q)=+1$ gilt, sind die Basen $\vec{e}_{1,2,3}$ und ${\vec {e}}'_{{1,2,3}}$ gleich orientiert und es liegt eine eigentliche euklidische Transformation vor.

Aktive Interpretation oder koordinatenfreie Abbildung

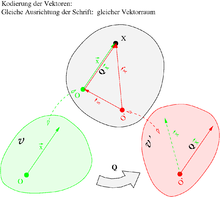
Veranschaulichung der aktiven Interpretation der euklidischen Transformation

Ein Beobachter wird meist sowohl einen anderen Ursprung als auch eine andere Zuordnung ${\mathcal {V}}':{\mathbb {E}}^{3}\times {\mathbb {E}}^{3}\mapsto {\mathbb {V}}^{3}$ des euklidischen Punktraums zu einem Vektorraum wählen als ein anderer Beobachter. Die Bilder von ${\mathcal {V}}$ und ${\mathcal {V}}'$ können höchstens verdreht sein, weil die Abbildung längentreu sein soll und eine Verschiebung hier nicht ins Gewicht fällt, da allen parallelen, gleichsinnigen und gleichlangen Verschiebungen von Punkten nach Punkten derselbe Vektor zugeordnet wird:

${\mathcal {V}}'(R,S)={\mathbf {Q}}\cdot {\mathcal {V}}(R,S)\quad \forall \;R,S\in {\mathbb {E}}^{3}$

worin $\mathbf {Q}$ ein orthogonaler Tensor ist ( ${\mathbf {Q}}^{\top }\cdot {\mathbf {Q}}={\mathbf {I}}$ mit Einheitstensor $\mathbf {I}$ ), siehe Bild. Nun ist

${\begin{array}{l}{\vec {x}}'={\mathcal {V}}'(O',X)={\mathcal {V}}'(O',O)+{\mathcal {V}}'(O,X)=\underbrace {{\mathcal {V}}'(O',O)}_{{{\vec {s}}}}+{\mathbf {Q}}\cdot \underbrace {{\mathcal {V}}(O,X)}_{{{\vec {x}}}}\\\rightarrow {\vec {x}}'={\vec {s}}+{\mathbf {Q}}\cdot {\vec {x}}\,.\end{array}}$

Diese Vektorgleichung ist koordinatenfrei, bezieht sich also auf kein Koordinaten- oder Basissystem. Anders als in der passiven Interpretation wird hier die Fähigkeit von Tensoren (hier $\mathbf {Q}$ ) ausgenutzt, Vektoren von einem Vektorraum (dem Bildraum von ${\mathcal {V}}$ ) in einen anderen, den Bildraum von ${\mathcal {V}}'$ , abzubilden, wobei in diesem Fall die beiden Bildräume identisch sind. Falls ${\mathrm {det}}({\mathbf {Q}})=+1$ liegt wiederum eine eigentliche euklidische Transformation vor. Weil jeder Tensor eine lineare Abbildung ist, entspricht dieses Vorgehen der Beschreibung mit Hilfe von linearen Abbildungen.

Der scheinbare Widerspruch $\mathbf{Q}\cdot\vec{x} =\vec{x}$ löst sich auf, wenn die verschiedenen Basissysteme links und rechts des Gleichheitszeichens berücksichtigt werden:

$\mathbf{Q}\cdot\sum_{i=1}^3 x_i\vec{e}'_i =\sum_{i=1}^3 x_i\vec{e}_i \quad\Leftrightarrow\quad \mathbf{Q}\cdot\vec{e}'_i =\vec{e}_i$

womit $\mathbf {Q}$ die komponentenweise Darstellung

$\mathbf{Q} =\sum_{i=1}^3\vec{e}_i\otimes\vec{e}'_i =\sum_{i,j=1}^3 (\vec{e}'_i\cdot\vec{e}_j)\vec{e}_i\otimes\vec{e}_j =\sum_{i,j=1}^3 Q_{ij}\vec{e}_i\otimes\vec{e}_j$

mit $Q_{ij}$ wie in der passiven Interpretation, bekommt, was die Äquivalenz der passiven und aktiven Interpretationen unterstreicht.

Transformation der Zeit

Ein Beobachterwechsel beinhaltet auch einen Wechsel im Zeitmaßstab. In der euklidischen Transformation ist nur eine konstante Versetzung $\Delta t$ vorgesehen:

$t'=t+\Delta t$

was so zu verstehen ist, dass die Beobachter zum selben Zeitpunkt verschiedene Werte auf ihren Uhren ablesen, die Differenz der Werte aber immer dieselbe ist. Die Beobachter haben also ihre Stoppuhren zu verschiedenen Zeiten gestartet.

Allgemeiner Beobachterwechsel

Ein allgemeiner Beobachterwechsel lässt sich also mathematisch wie folgt beschreiben:

${\begin{array}{lll}{\vec {x}}'(t')&=&{\vec {s}}(t)+{\mathbf {Q}}(t)\cdot {\vec {x}}(t)\\t'&=&t+\Delta t\\{\mathbf {Q}}(t)\cdot {\mathbf {Q}}^{\top }(t)&=&{\mathbf {Q}}^{\top }(t)\cdot {\mathbf {Q}}(t)={\mathbf {I}},\quad {\mathrm {det}}({\mathbf {Q}})=+1\,,\end{array}}$

weil Drehspiegelungen (mit ${\mathrm {det}}({\mathbf {Q}})=-1$ ) unphysikalisch sind. Die Galilei-Transformation ist hierin als der Spezialfall der gleichförmigen Bewegung

${\ddot {{\vec {s}}}}(t)={\vec {0}}\Leftrightarrow {\vec {s}}(t)={{\vec {s}}}_{{0}}+{{\vec {v}}}_{{0}}t$ und ${\mathbf {Q}}(t)={\mathbf {Q}}_{{0}}={\mathrm {const.}}$

enthalten, worin ${{\vec {s}}}_{{0}}$ eine konstante Verschiebung, ${{\vec {v}}}_{{0}}$ eine konstante Geschwindigkeit und ${\mathbf {Q}}_{{0}}$ eine konstante Verdrehung benennen.

Objektive oder invariante Größen

Größen, die bei einem Wechsel des Bezugssystems unverändert wahrgenommen werden, werden objektiv oder invariant genannt. Einführend sei der Abstand zweier Punkte betrachtet: Bei jeder euklidischen Transformation bleibt der Abstand zwischen zwei beliebigen Punkten immer konstant und das gilt auch beim allgemeinen Beobachterwechsel. Seien ${\vec {p}}={\mathcal {V}}(O,P)$ und ${\vec {q}}={\mathcal {V}}(O,Q)$ die Ortsvektoren zweier Punkte . Das Quadrat ihres Abstandes

${\begin{array}{lcl}d'^{2}&=&({\vec {p}}'-{\vec {q}}')\cdot ({\vec {p}}'-{\vec {q}}')=({\vec {s}}+{\mathbf {Q}}\cdot {\vec {p}}-{\vec {s}}-{\mathbf {Q}}\cdot {\vec {q}})\cdot ({\vec {s}}+{\mathbf {Q}}\cdot {\vec {p}}-{\vec {s}}-{\mathbf {Q}}\cdot {\vec {q}})=[{\mathbf {Q}}\cdot ({\vec {p}}-{\vec {q}})]\cdot [{\mathbf {Q}}\cdot ({\vec {p}}-{\vec {q}})]\\&=&({\vec {p}}-{\vec {q}})\cdot {\mathbf {Q^{\top }\cdot Q}}\cdot ({\vec {p}}-{\vec {q}})=({\vec {p}}-{\vec {q}})\cdot ({\vec {p}}-{\vec {q}})={d}^{2}\end{array}}$

bleibt also unverändert, wenn ${\mathbf {Q^{\top }\cdot Q}}={\mathbf {I}}$ ist und sich der Abstandsvektor ${\vec {p}}-{\vec {q}}$ gemäß

$({\vec {p}}-{\vec {q}})'={\mathbf {Q}}\cdot ({\vec {p}}-{\vec {q}})$

transformiert. Letzteres kennzeichnet objektive Vektoren. Die Transformationseigenschaft für objektive Tensoren leitet sich aus der Forderung ab, dass ein objektiver Tensor objektive Vektoren auf objektive Vektoren abbildet. Bei objektiven Vektoren ${\vec {v}}$ und $\vec{w}$ soll also ${\vec {w}}\cdot {\mathbf {T}}\cdot {\vec {v}}$ ebenfalls objektiv sein. Aus ${\vec {v}}'={\mathbf {Q}}\cdot {\vec {v}}$ , ${\vec {w}}'={\mathbf {Q}}\cdot {\vec {w}}$ und ${\vec {w}}'\cdot {\mathbf {T}}'\cdot {\vec {v}}'={\vec {w}}\cdot {\mathbf {T}}\cdot {\vec {v}}$ resultiert:

${\vec {w}}\cdot {\mathbf {T}}\cdot {\vec {v}}=({\mathbf {Q}}^{\top }\cdot {\vec {w}}')\cdot {\mathbf {T\cdot Q}}^{\top }\cdot {\vec {v}}'={\vec {w}}'\cdot {\mathbf {Q\cdot T\cdot Q}}^{\top }\cdot {\vec {v}}'={\vec {w}}'\cdot {\mathbf {T}}'\cdot {\vec {v}}'\,.$

Soll dies für alle objektiven Vektoren ${\vec {v}}$ und $\vec{w}$ gelten, so muss sich der Tensor gemäß

${\mathbf {T}}'={\mathbf {Q\cdot T\cdot Q}}^{\top }$

transformieren.

Transformationseigenschaften objektiver Größen

Eine Größe ist objektiv, wenn sie sich bei einem Beobachterwechsel wie folgt transformiert:

Typ	Bedingung
Skalar $\phi '(t')=\phi (t)$
Vektor ${\vec {v}}$	${\vec {v}}'(t')={\mathbf {Q}}(t)\cdot {\vec {v}}(t)$
Tensor $\mathbf {T}$	${\mathbf {T}}'(t')={\mathbf {Q}}(t)\cdot {\mathbf {T}}(t)\cdot {\mathbf {Q}}^{\top }(t)$

Geschwindigkeiten und Beschleunigung

Die Geschwindigkeit ist wegen

${\vec {v}}'={\frac {{\mathrm {d}}}{{\mathrm {d}}t'}}({\vec {s}}+{\mathbf {Q}}\cdot {\vec {x}})={\frac {{\mathrm {d}}}{{\mathrm {d}}t}}({\vec {s}}+{\mathbf {Q}}\cdot {\vec {x}})={\dot {{\vec {s}}}}+{\dot {{\mathbf {Q}}}}\cdot {\vec {x}}+{\mathbf {Q}}\cdot {\vec {v}}\neq {\mathbf {Q}}\cdot {\vec {v}}$

keine objektive Größe und gleiches gilt für die Beschleunigung:

${\vec {a}}'={\frac {{\mathrm {d}}{\vec {v}}'}{{\mathrm {d}}t'}}={\frac {{\mathrm {d}}}{{\mathrm {d}}t}}({\dot {{\vec {s}}}}+{\dot {{\mathbf {Q}}}}\cdot {\vec {x}}+{\mathbf {Q}}\cdot {\vec {v}})={\ddot {{\vec {s}}}}+{\ddot {{\mathbf {Q}}}}\cdot {\vec {x}}+{\dot {{\mathbf {Q}}}}\cdot {\vec {v}}+{\dot {{\mathbf {Q}}}}\cdot {\vec {v}}+{\mathbf {Q}}\cdot {\vec {a}}={\ddot {{\vec {s}}}}+{\ddot {{\mathbf {Q}}}}\cdot {\vec {x}}+2{\dot {{\mathbf {Q}}}}\cdot {\vec {v}}+{\mathbf {Q}}\cdot {\vec {a}}\neq {\mathbf {Q}}\cdot {\vec {a}}\,.$

Nur im Spezialfall der Galilei-Transformation ist wegen ${\ddot {{\vec {s}}}}={\vec {0}}$ und ${\ddot {{\mathbf {Q}}}}={\dot {{\mathbf {Q}}}}={\mathbf {0}}$ die Beschleunigung objektiv. Es kann aber gezeigt werden, dass die Absolutgeschwindigkeit und die Absolutbeschleunigung objektiv sind.

Die Zeitableitung eines objektiven Vektors $\vec{w}$ ist wegen

$({\vec {w}}'){\dot {}}=({\mathbf {Q}}\cdot {\vec {w}}){\dot {}}={\dot {{\mathbf {Q}}}}\cdot {\vec {w}}+{\mathbf {Q}}\cdot {\dot {{\vec {w}}}}\neq {\mathbf {Q}}\cdot {\dot {{\vec {w}}}}$

meist nicht objektiv und gleiches gilt für die Zeitableitung eines objektiven Tensors $\mathbf {T}$ :

$({\mathbf {T}}'){\dot {}}=({\mathbf {Q\cdot T\cdot Q}}^{\top }){\dot {}}={\dot {{\mathbf {Q}}}}\cdot {\mathbf {T\cdot Q}}^{\top }+{\mathbf {Q}}\cdot {\dot {{\mathbf {T}}}}\cdot {\mathbf {Q}}^{\top }+{\mathbf {Q\cdot T}}\cdot {\dot {{\mathbf {Q}}}}^{\top }\neq {\mathbf {Q}}\cdot {\dot {{\mathbf {T}}}}\cdot {\mathbf {Q}}^{\top }\,.$

Für die Formulierung ratenabhängiger Materialmodelle werden in der räumlichen Betrachtungsweise objektive Zeitableitungen für konstitutive Variablen benötigt, denn es entspricht nicht der Erfahrung, dass ein bewegter Beobachter ein anderes Materialverhalten misst als ein ruhender. Somit müssen die Materialmodelle mit objektiven Zeitableitungen formuliert werden. Der Deformationsgradient $\mathbf {F}$ beschreibt die lokalen Verformungen an einem Punkt im Material und entsprechend enthält er auch alle Informationen zu Verformungsraten. Es wird der räumliche Geschwindigkeitsgradient

${\mathbf {l}}:={\dot {{\mathbf {F}}}}\cdot {\mathbf {F}}^{{-1}}={\mathbf {d}}+{\mathbf {w}}$

definiert, dessen symmetrischer Anteil

${\mathbf {d}}:={\frac 12}({\mathbf {l}}+{\mathbf {l}}^{\top })$

räumlicher Verzerrungsgeschwindigkeitstensor und dessen unsymmetrische Anteil

${\mathbf {w}}:={\frac 12}({\mathbf {l}}-{\mathbf {l}}^{\top })$

Wirbeltensor oder Spintensor heißt. Diese Tensoren werden, weil sie räumlich formuliert sind, klein geschrieben. In der Materialtheorie interessieren besonders objektive Raten von Verzerrungstensoren und Spannungstensoren. Es wurden mehrere Raten definiert, unter anderem^[2]:

Zaremba-Jaumann Ableitung: ${\stackrel {\circ }{{\mathbf {T}}}}:={\dot {{\mathbf {T}}}}+{\mathbf {T\cdot w}}-{\mathbf {w\cdot T}}$

Kovariante Oldroyd Ableitung: ${\stackrel {\triangle }{{\mathbf {T}}}}:={\dot {{\mathbf {T}}}}+{\mathbf {T\cdot l}}+{\mathbf {l}}^{\top }\cdot {\mathbf {T}}={\stackrel {\circ }{{\mathbf {T}}}}+{\mathbf {T\cdot d}}+{\mathbf {d\cdot T}}$

Kontravariante Oldroyd Ableitung: ${\stackrel {\nabla }{{\mathbf {T}}}}:={\dot {{\mathbf {T}}}}-{\mathbf {l\cdot T}}-{\mathbf {T}}\cdot {\mathbf {l}}^{\top }={\stackrel {\circ }{{\mathbf {T}}}}-{\mathbf {T\cdot d}}-{\mathbf {d\cdot T}}$

Cauchy-Ableitung^[4]: ${\stackrel {\diamond }{{\mathbf {T}}}}={\dot {{\mathbf {T}}}}+\operatorname {Sp}({\mathbf {l}}){\mathbf {T}}-{\mathbf {l\cdot T}}-{\mathbf {T\cdot l}}^{\top }\,.$

Die Zaremba-Jaumann Spannungs-Geschwindigkeit gibt die zeitliche Änderung der Spannungen im bewegten Bezugssystem an. Ein Beobachter, der mit dem materiellen Element rotiert, stellt die zeitliche Änderung $\stackrel{\circ}{\mathbf{T}}$ der Spannungen $\mathbf {T}$ fest.

Für einen objektiven Vektor ${\vec {v}}$ sind die Zeitableitungen

${\begin{array}{rclcl}{\stackrel {\circ }{{\vec {v}}}}&=&{\dot {{\vec {v}}}}-{\mathbf {w}}\cdot {\vec {v}}\\{\stackrel {\Delta }{{\vec {v}}}}&=&{\dot {{\vec {v}}}}+{\mathbf {l}}^{\top }\cdot {\vec {v}}&=&{\stackrel {\circ }{{\vec {v}}}}+{\mathbf {d}}\cdot {\vec {v}}\\{\stackrel {\nabla }{{\vec {v}}}}&=&{\dot {{\vec {v}}}}-{\mathbf {l}}\cdot {\vec {v}}&=&{\stackrel {\circ }{{\vec {v}}}}-{\mathbf {d}}\cdot {\vec {v}}\end{array}}$

objektiv.

Objektivität und algebraische Verknüpfungen

Eine algebraische Verknüpfung von objektiven Größen ist wieder objektiv. Als algebraische Verknüpfung kommt je nach Typ Addition, Multiplikation, Multiplikation mit einem Skalar, Skalarprodukt, Kreuzprodukt, dyadisches Produkt und Matrizenmultiplikation in Frage.

Operation	Gleichung
Skalare
Addition
Multiplikation	$(a\cdot b)'=a'\cdot b'=a\cdot b$
Vektoren
Addition	$({\vec {x}}+{\vec {y}})'={\mathbf {Q}}\cdot {\vec {x}}+{\mathbf {Q}}\cdot {\vec {y}}={\mathbf {Q}}\cdot ({\vec {x}}+{\vec {y}})$
Multiplikation mit einem Skalar	$(a{\vec {x}})'=a'{\vec {x}}'=a{\mathbf {Q}}\cdot {\vec {x}}={\mathbf {Q}}\cdot (a{\vec {x}})$
Skalarprodukt	$({\vec {x}}\cdot {\vec {y}})'={\vec {x}}'\cdot {\vec {y}}'=({\mathbf {Q}}\cdot {\vec {x}})\cdot ({\mathbf {Q}}\cdot {\vec {y}})={\vec {x}}\cdot {\mathbf {Q}}^{\top }\cdot {\mathbf {Q}}\cdot {\vec {y}}={\vec {x}}\cdot {\vec {y}}$
Kreuzprodukt	$({\vec {x}}\times {\vec {y}})'={\vec {x}}'\times {\vec {y}}'=({\mathbf {Q}}\cdot {\vec {x}})\times ({\mathbf {Q}}\cdot {\vec {y}})={\mathbf {Q}}\cdot ({\vec {x}}\times {\vec {y}})$
Dyadisches Produkt	$({\vec {x}}\otimes {\vec {y}})'={\vec {x}}'\otimes {\vec {y}}'={\mathbf {Q}}\cdot {\vec {x}}\otimes {\mathbf {Q}}\cdot {\vec {y}}={\mathbf {Q}}\cdot ({\vec {x}}\otimes {\vec {y}})\cdot {\mathbf {Q}}^{\top }$
Tensoren
Addition	$({\mathbf {S}}+{\mathbf {T}})'={\mathbf {Q\cdot S\cdot Q}}^{\top }+{\mathbf {Q\cdot T\cdot Q}}^{\top }={\mathbf {Q}}\cdot ({\mathbf {S}}+{\mathbf {T}})\cdot {\mathbf {Q}}^{\top }$
Multiplikation mit einem Skalar	$(a{\mathbf {T}})'=a'{\mathbf {T}}'=a{\mathbf {Q\cdot T\cdot Q}}^{\top }={\mathbf {Q}}\cdot (a{\mathbf {T}})\cdot {\mathbf {Q}}^{\top }$
Skalarprodukt	$({\mathbf {S}}:{\mathbf {T}})'=({\mathbf {Q\cdot S\cdot Q}}^{\top }):({\mathbf {Q\cdot T\cdot Q}}^{\top })={\mathbf {S}}:{\mathbf {T}}$
Vektortransformation	$({\mathbf {T}}\cdot {\vec {x}})'={\mathbf {T}}'\cdot {\vec {x}}'=({\mathbf {Q\cdot T\cdot Q}}^{\top })\cdot ({\mathbf {Q}}\cdot {\vec {x}})={\mathbf {Q}}\cdot ({\mathbf {T}}\cdot {\vec {x}})$
Matrizenmultiplikation	$({\mathbf {S\cdot T}})'=({\mathbf {Q\cdot S\cdot Q}}^{\top })\cdot ({\mathbf {Q\cdot T\cdot Q}}^{\top })={\mathbf {Q}}\cdot ({\mathbf {S\cdot T}})\cdot {\mathbf {Q}}^{\top }$

Liste objektiver Größen

Die folgende Aufstellung gibt eine Auswahl an objektiven Größen.

Skalare

Geometrie: Abstand, Flächeninhalt (Betrag), Volumen (Betrag). Die Volumenform ist nur bei eigentlichen euklidischen Transformationen mit ${\mathrm {det}}({\mathbf {Q}})=+1$ objektiv.
Physik: Temperatur, Masse, Innere Energie und Entropie sind objektive Skalare. Hieraus kann abgeleitet werden, dass auch die auf die Masse oder das Volumen bezogenen spezifischen Größen objektiv sind: Dichte, spezifische innere Energie und spezifische Entropie.

Vektoren

Geometrie: Abstandsvektor, Linienelement; das Oberflächenelement ist nur bei eigentlichen euklidischen Transformationen mit ${\mathrm {det}}({\mathbf {Q}})=+1$ objektiv.
Kinematik: absolute Geschwindigkeit, absolute Beschleunigung
Physik: Kraft, Spannungsvektor, Wärmeflussvektor und der Temperaturgradient

Tensoren

Die obige Transformationseigenschaften für Tensoren gelten für sogenannte räumliche ein-Feld-Tensoren, deren Definitions- und Wertebereich mit der Bewegung rotieren. Daneben existieren in der Kontinuumsmechanik körperbezogene ein-Feld Tensoren, deren Definitions- und Wertebereich durch die Referenzkonfiguration bewegungsunabhängig materiell festgelegt ist, die also für alle Beobachter gleich ist. Die Bildvektoren dieser Konfigurationen sind – anschaulich gesprochen – für alle Beobachter wie ein Etikett lesbar an einen materiellen Punkt geheftet. Objektive Tensoren diesen Typs transformieren sich gemäß

${\mathbf {T}}{'}={\mathbf {T}}\,.$

Des Weiteren kennt die Kontinuumsmechanik zwei-Feld-Tensoren, die Vektoren und Tensoren zwischen zwei Konfigurationen transformieren. Ein Beispiel hierfür ist der erste Piola-Kirchhoff Spannungstensor, der in konvektiven Koordinaten die Form

${\mathbf {T}}=\sum _{{i,j=1}}^{3}T^{{ij}}{\vec {g}}_{i}\otimes {\vec {G}}_{j}$

besitzt. Darin sind ${\vec {G}}_{{1,2,3}}$ Basisvektoren in der bewegungsunabhängigen materiellen Referenzkonfiguration, ${\vec {g}}_{{1,2,3}}$ Basisvektoren in der bewegten räumlichen Momentankonfiguration und $T^{ij}$ die Komponenten des Tensors. Wenn nun die Basisvektoren ${\vec {G}}_{i}$ für alle Beobachter gleich sind, d.h. es gilt

${\vec {G}}_{i}'={\vec {G}}_{i}\quad \forall \;i=1,2,3\,,$

und die Basisvektoren ${\vec {g}}_{i}$ objektiv sind, sich also gemäß

$\vec{g}_i'=\mathbf{Q}\cdot\vec{g}_i\quad\forall\; i=1,2,3$

transformieren, dann ist also ein solcher zwei-Feld-Tensor $\mathbf {T}$ objektiv, wenn er sich gemäß

${\mathbf {T}}{'}=\sum _{{i,j=1}}^{3}T^{{ij}}{'}{\vec {g}}_{i}{'}\otimes {\vec {G}}_{j}{'}=\sum _{{i,j=1}}^{3}T^{{ij}}{\mathbf {Q}}\cdot {\vec {g}}_{i}\otimes {\vec {G}}_{j}={\mathbf {Q\cdot T}}\,,$

also wie ein objektiver Vektor transformiert.

Die folgenden Tensoren werden auf den Seiten Strecktensor, Verzerrungstensor, Geschwindigkeitsgradient, Spannungstensor und Kontinuumsmechanik erwähnt. Weil spiegelnde Transformationen materieller Körper in der Realität nicht vorkommen wird ${\mathrm {det}}({\mathbf {Q}})=+1$ vorausgesetzt.

Name	Nicht objektiv	Objektiv (allgemein)	Körperbezogen objektiv	Objektiver zwei-Feld Tensor
Deformationsgradient ${\mathbf {F}}={\mathbf {R\cdot U}}={\mathbf {v\cdot R}}$				${\mathbf {F}}'={\mathbf {Q\cdot F}}$
Rechter Strecktensor $\mathbf{U}$			x
Linker Strecktensor $\mathbf {v}$		x
Rotationstensor $\mathbf{R}$				${\mathbf {R}}'={\mathbf {Q\cdot R}}$
Rechter Cauchy-Green Tensor ${\mathbf {C}}={\mathbf {F}}^{\top }\cdot {\mathbf {F}}={\mathbf {U\cdot U}}$			x
Linker Cauchy-Green Tensor ${\mathbf {b}}={\mathbf {F\cdot F}}^{\top }={\mathbf {v\cdot v}}$		x
Green-Lagrange-Verzerrungstensor ${\mathbf {E}}={\frac 12}({\mathbf {F}}^{\top }\cdot {\mathbf {F}}-{\textbf {I}})$			x
Euler-Almansi-Verzerrungstensor ${\mathbf {e}}={\frac 12}({\textbf {I}}-{\mathbf {F}}^{{\top -1}}\cdot {\mathbf {F}}^{{-1}})$		x
Cauchy’scher Spannungstensor ${\boldsymbol {\sigma }}$		x
Erster Piola-Kirchoff’scher Spannungstensor ${\mathbf {P}}={\mathrm {det}}({\mathbf {F}}){\boldsymbol {\sigma }}\cdot {\mathbf {F}}^{{\top -1}}$				${\mathbf {P}}'={\mathbf {Q\cdot P}}$
Zweiter Piola-Kirchoff’scher Spannungstensor ${\tilde {{\mathbf {T}}}}={\mathrm {det}}({\mathbf {F}}){\mathbf {F}}^{{-1}}\cdot {\boldsymbol {\sigma }}\cdot {\mathbf {F}}^{{\top -1}}$			x
Geschwindigkeiten
Räumlicher Geschwindigkeitsgradient ${\mathbf {l}}={\mathrm {grad}}({\vec {v}}({\vec {x}},t))={\dot {{\mathbf {F}}}}\cdot {\mathbf {F}}^{{-1}}$	${\mathbf {l}}'={\mathbf {Q\cdot l\cdot Q}}^{\top }+{\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top }$
Räumlicher Verzerrungsgeschwindigkeitstensor ${\mathbf {d}}={\frac {1}{2}}({\mathbf {l}}+{\mathbf {l}}^{\top })$		x
Spintensor ${\mathbf {w}}={\frac {1}{2}}({\mathbf {l}}-{\mathbf {l}}^{\top })$	${\mathbf {w}}'={\mathbf {Q\cdot w\cdot Q}}^{\top }+{\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top }$
Materieller Verzerrungsgeschwindigkeitstensor ${\dot {{\mathbf {E}}}}$			x
Materielle Zeitableitung ${\dot {{\mathbf {e}}}}$ von $\mathbf{e}$	längere Formel
Oldroyd Ableitung der Euler-Almansi-Dehnungen ${\stackrel {\triangle }{{\mathbf {e}}}}={\mathbf {d}}$		x

Beispiel

Es wird der Nachweis der Objektivität der Zaremba-Jaumann Rate eines objektiven Tensors gegeben. Zu zeigen ist

$({\stackrel {\circ }{{\mathbf {T}}}})'={\mathbf {Q}}\cdot {\stackrel {\circ }{{\mathbf {T}}}}\cdot {\mathbf {Q}}^{\top }={\mathbf {Q}}\cdot ({\dot {{\mathbf {T}}}}+{\mathbf {T\cdot w}}-{\mathbf {w\cdot T}})\cdot {\mathbf {Q}}^{\top }\,.$

Mit

${\mathbf {w}}'={\mathbf {Q\cdot w\cdot Q}}^{\top }+{\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top }$

und

bekommt man

${\begin{array}{lcl}({\stackrel {\circ }{{\mathbf {T}}}})'&=&{\dot {{\mathbf {T}}}}'+{\mathbf {T}}'\cdot {\mathbf {w}}'-{\mathbf {w}}'\cdot {\mathbf {T}}'\\&=&({\dot {{\mathbf {Q}}}}\cdot {\mathbf {T\cdot Q}}^{\top }+{\mathbf {Q}}\cdot {\dot {{\mathbf {T}}}}\cdot {\mathbf {Q}}^{\top }+{\mathbf {Q\cdot T}}\cdot {\dot {{\mathbf {Q}}}}^{\top })+({\mathbf {Q\cdot T\cdot Q}}^{\top })\cdot ({\mathbf {Q\cdot w\cdot Q}}^{\top }+{\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top })\\&&-({\mathbf {Q\cdot w\cdot Q}}^{\top }+{\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top })\cdot ({\mathbf {Q\cdot T\cdot Q}}^{\top })\\&=&{\dot {{\mathbf {Q}}}}\cdot {\mathbf {T\cdot Q}}^{\top }+{\mathbf {Q}}\cdot {\dot {{\mathbf {T}}}}\cdot {\mathbf {Q}}^{\top }+{\mathbf {Q\cdot T}}\cdot {\dot {{\mathbf {Q}}}}^{\top }+{\mathbf {Q\cdot T\cdot w\cdot Q}}^{\top }\\&&+{\mathbf {Q\cdot T\cdot Q}}^{\top }\cdot {\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top }-{\mathbf {Q\cdot w\cdot T\cdot Q}}^{\top }-{\dot {{\mathbf {Q}}}}\cdot {\mathbf {T\cdot Q}}^{\top }\\&=&{\mathbf {Q}}\cdot ({\dot {{\mathbf {T}}}}+{\mathbf {T\cdot w}}-{\mathbf {w\cdot T}})\cdot {\mathbf {Q}}^{\top }+{\mathbf {Q\cdot T}}\cdot {\dot {{\mathbf {Q}}}}^{\top }+{\mathbf {Q\cdot T\cdot Q}}^{\top }\cdot {\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top }\\&=&{\mathbf {Q}}\cdot {\stackrel {\circ }{{\mathbf {T}}}}\cdot {\mathbf {Q}}^{\top }+{\mathbf {Q\cdot T}}\cdot {\dot {{\mathbf {Q}}}}^{\top }+{\mathbf {Q\cdot T\cdot Q}}^{\top }\cdot {\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top }\,.\end{array}}$

Nun kann man

${\dot {{\mathbf {I}}}}=({\mathbf {Q\cdot Q}}^{\top }){\dot {}}={\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top }+{\mathbf {Q}}\cdot {\dot {{\mathbf {Q}}}}^{\top }={\mathbf {0}}\rightarrow {\dot {{\mathbf {Q}}}}\cdot {\mathbf {Q}}^{\top }=-{\mathbf {Q}}\cdot {\dot {{\mathbf {Q}}}}^{\top }$

ausnutzen und erhält

${\begin{array}{rcl}({\stackrel {\circ }{{\mathbf {T}}}})'&=&{\mathbf {Q}}\cdot {\stackrel {\circ }{{\mathbf {T}}}}\cdot {\mathbf {Q}}^{\top }+{\mathbf {Q\cdot T}}\cdot {\dot {{\mathbf {Q}}}}^{\top }-{\mathbf {Q\cdot T\cdot Q}}^{\top }\cdot {\mathbf {Q}}\cdot {\dot {{\mathbf {Q}}}}^{\top }\\&=&{\mathbf {Q}}\cdot {\stackrel {\circ }{{\mathbf {T}}}}\cdot {\mathbf {Q}}^{\top }+{\mathbf {Q\cdot T}}\cdot {\dot {{\mathbf {Q}}}}^{\top }-{\mathbf {Q\cdot T}}\cdot {\dot {{\mathbf {Q}}}}^{\top }={\mathbf {Q}}\cdot {\stackrel {\circ }{{\mathbf {T}}}}\cdot {\mathbf {Q}}^{\top }\,,\end{array}}$

also das gewünschte Ergebnis.

Siehe auch

Fußnoten

↑ Der "aktive" und "passive" Beobachterwechsel sind nicht zu verwechseln mit der aktiven Bewegung, bei der sich ein Objekt bewegt, und der passiven Bewegung, bei der sich der Beobachter relativ zum ruhenden Objekt bewegt.
↑ Die Formelzeichen für die objektiven Raten variieren von Quelle zu Quelle. Die hier angegebenen folgen P. Haupt, S. 48ff. In H. Altenbach wird $\mathbf{T}^\nabla$ für $\stackrel{\circ}{\mathbf{T}}$ und $\mathbf{T}^O$ für $\stackrel{\triangle}{\mathbf{T}}$ benutzt.
↑ Diese Ableitung kommt in der Cauchy-Elastizität vor und wird auch nach C. Truesdell benannt. Er selbst benannte die Ableitung aber nach Cauchy und schrieb 1963, dass diese Rate ohne erfindlichen Grund nach ihm benannt wurde ( „came to be named, for no good reason, after [...] me“ ) siehe C. Truesdell: Remarks on Hypo-Elasticity, Journal of Research of the National Bureau of Standards - B. Mathematics and Mathematical Physics, Vol. 67B, No. 3, July-September 1963, S. 141.

Basierend auf Artikeln in:

Wikipedia.de