Strecktensor

Strecktensoren oder Deformationstensoren sind einheitenfreie Tensoren (bestimmte mathematische Objekte der linearen Algebra) zweiter Stufe, die lokale Distanzänderungen von Materieelementen bei einer Deformation eines Körpers bemessen. Distanzänderungen von Materieelementen entsprechen der Streckung bzw. Stauchung der materiellen Linien, die die betrachteten Materieelemente verbinden. Diese Änderungen der inneren Anordnung korrespondieren mit einer Änderung der äußeren Gestalt des Festkörpers und werden beispielsweise als Dehnung oder Stauchung sichtbar.

Die Strecktensoren sind eine wesentliche Größe in der Beschreibung der Kinematik der Deformation und in der Kontinuumsmechanik werden eine Reihe von verschiedenen Strecktensoren definiert, die ihrerseits der Definition von Verzerrungstensoren dienen. In einigen Materialmodellen der Hyperelastizität werden Strecktensoren direkt eingesetzt.

Streckung von Linienelementen

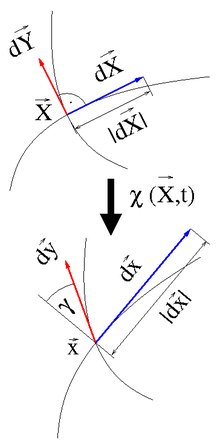
Streckung und Scherung der Tangenten (rot und blau) an materielle Linien (schwarz) im Zuge einer Deformation

Bei der quantitativen Beurteilung einer Deformation eines Körpers werden materielle Linien des Körpers vor und nach Deformation miteinander verglichen. In der Praxis können dazu Dehnungsmessstreifen (DMS) auf dem Körper aufgeklebt werden. Die Richtung des DMS wird mathematisch mit einem materiellen Linienelement ${\mathrm {d}}{\vec {X}}$ in der undeformierten Ausgangskonfiguration und ${\mathrm {d}}{\vec {x}}$ in der deformierten Momentankonfiguration beschrieben, siehe Abbildung rechts. Diese Linienelemente stehen in linearer Näherung über den Deformationsgradient $\mathbf {F}$ in Beziehung:

${\mathrm {d}}{\vec {x}}={\mathbf {F}}\cdot {\mathrm {d}}{\vec {X}}$

Die Streckung $\lambda$ eines Linienelementes in der Richtung

${\vec {e}}={\frac {{\mathrm {d}}{\vec {X}}}{|{\mathrm {d}}{\vec {X}}|}}$

ist das Verhältnis

$\lambda ={\frac {|{\mathrm {d}}{\vec {x}}|}{|{\mathrm {d}}{\vec {X}}|}}={\sqrt {{\frac {{\mathrm {d}}{\vec {x}}\cdot {\mathrm {d}}{\vec {x}}}{{\mathrm {d}}{\vec {X}}\cdot {\mathrm {d}}{\vec {X}}}}}}={\sqrt {{\frac {({\mathbf {F}}\cdot {\mathrm {d}}{\vec {X}})\cdot ({\mathbf {F}}\cdot {\mathrm {d}}{\vec {X}})}{{\mathrm {d}}{\vec {X}}\cdot {\mathrm {d}}{\vec {X}}}}}}={\sqrt {{\vec {e}}\cdot {\mathbf {C}}\cdot {\vec {e}}}}$

Der Strecktensor

${\mathbf {C}}={\mathbf {F}}^{\top }\cdot {\mathbf {F}}$

heißt rechter Cauchy-Green Tensor und ist demnach ein Maß für die Streckung von Linienelementen. Das Superskript „ $\top$ “ steht für die Transposition. In Richtung der Eigenvektoren von ${\mathbf {C}}$ sind die Streckungen extremal. In der deformierten Lage berechnet sich die Streckung aus

$\lambda ={\sqrt {{\frac {{\mathrm {d}}{\vec {x}}\cdot {\mathrm {d}}{\vec {x}}}{({\mathbf {F}}^{{-1}}\cdot {\mathrm {d}}{\vec {x}})\cdot ({\mathbf {F}}^{{-1}}\cdot {\mathrm {d}}{\vec {x}})}}}}=\left({\frac {{\mathrm {d}}{\vec {x}}}{|{\mathrm {d}}{\vec {x}}|}}\cdot {\mathbf {c}}\cdot {\frac {{\mathrm {d}}{\vec {x}}}{|{\mathrm {d}}{\vec {x}}|}}\right)^{{-{\frac {1}{2}}}}\,.$

Der Cauchysche Strecktensor

${\mathbf {c}}:={\mathbf {F}}^{{\top -1}}\cdot {\mathbf {F}}^{{-1}}$

ist also ein räumliches Maß für die Streckung von Linienelementen.

Streckung von Normalvektoren

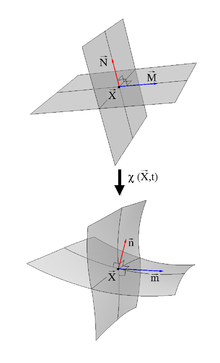
Streckung und Scherung der Normalen (rot und blau) an materielle Flächen (grau) im Zuge einer Deformation

Mit Strecktensoren kann auch die Streckung von Normalvektoren ermittelt werden. Eine Familie von Flächen kann durch eine skalare Funktion

$\Phi ({\vec {x}},t)=C$

und einen Flächenparameter definiert werden.

Die Normalenvektoren an diese Flächen sind die Gradienten

${\vec {n}}:=\operatorname {grad} (\Phi )=\sum _{i=1}^{3}{\frac {\mathrm {d} \Phi }{\mathrm {d} x_{i}}}{\vec {e}}_{i}\,.$

Diese hängen mit der Normale in der Referenzkonfiguration wie folgt zusammen:

${\begin{aligned}{\vec {N}}:=&\operatorname {GRAD} (\Phi )=\sum _{i=1}^{3}{\frac {\mathrm {d} \Phi }{\mathrm {d} X_{i}}}{\vec {e}}_{i}=\sum _{j,k=1}^{3}{\frac {\mathrm {d} \Phi }{\mathrm {d} x_{k}}}{\frac {\mathrm {d} x_{k}}{\mathrm {d} X_{j}}}{\vec {e}}_{j}\\=&\sum _{i,j,k=1}^{3}{\frac {\mathrm {d} \Phi }{\mathrm {d} x_{k}}}{\vec {e}}_{k}\cdot {\frac {\mathrm {d} x_{i}}{\mathrm {d} X_{j}}}{\vec {e}}_{i}\otimes {\vec {e}}_{j}={\vec {n}}\cdot \mathbf {F} =\mathbf {F} ^{\top }\cdot {\vec {n}}\\\rightarrow {\vec {n}}=&\mathbf {F} ^{\top -1}\cdot {\vec {N}}\end{aligned}}$

Das Rechenzeichen $\otimes$ bezeichnet das dyadische Produkt. Die Streckung der Normalvektoren in der deformierten und undeformierten Lage in einem materiellen Punkt $\vec{X}$ führt auf den Finger-Tensor

${\begin{array}{rcl}\lambda &=&\displaystyle {\frac {|{\vec {n}}|}{|{\vec {N}}|}}={\sqrt {{\frac {{\vec {n}}\cdot {\vec {n}}}{{\vec {N}}\cdot {\vec {N}}}}}}={\sqrt {{\frac {({\mathbf {F}}^{{\top -1}}\cdot {\vec {N}})\cdot ({\mathbf {F}}^{{\top -1}}\cdot {\vec {N}})}{{\vec {N}}\cdot {\vec {N}}}}}}={\sqrt {{\frac {{\vec {N}}}{|{\vec {N}}|}}\cdot {\mathbf {f}}\cdot {\frac {{\vec {N}}}{|{\vec {N}}|}}}}\\\rightarrow {\mathbf {f}}&=&{\mathbf {F}}^{{-1}}\cdot {\mathbf {F}}^{{\top -1}}={\mathbf {C}}^{{-1}}\,,\end{array}}$

der also ein Maß für die Streckung der materiellen Flächennormalen ist. Der Finger-Tensor operiert in der Ausgangskonfiguration.

Sein Gegenstück in der Momentankonfiguration ist der linke Cauchy-Green Tensor

${\mathbf {b}}={\mathbf {F}}\cdot {\mathbf {F}}^{\top }={\mathbf {c}}^{{-1}}$

für den

$\lambda ={\sqrt {{\frac {{\vec {n}}\cdot {\vec {n}}}{({\mathbf {F}}^{\top }\cdot {\vec {n}})\cdot ({\mathbf {F}}^{\top }\cdot {\vec {n}})}}}}=\left({\frac {{\vec {n}}}{|{\vec {n}}|}}\cdot {\mathbf {b}}\cdot {\frac {{\vec {n}}}{|{\vec {n}}|}}\right)^{{-{\frac {1}{2}}}}$

abgeleitet werden kann.

Hauptinvarianten des rechten Cauchy-Green Tensors

Bei einer Deformation werden die materiellen Linien-, Flächen- und Volumenelemente mit dem Deformationsgradient von der Ausgangskonfiguration in die Momentankonfiguration transformiert

${\begin{array}{rccl}{\mathrm {d}}{\vec {x}}&=&{\mathbf {F}}&\cdot \;{\mathrm {d}}{\vec {X}}\\{\vec {n}}\,{\mathrm {d}}a&=&\operatorname {cof}({\mathbf {F}})&\cdot \;{\vec {N}}\,{\mathrm {d}}A\\{\mathrm {d}}v&=&\operatorname {det}({\mathbf {F}})&{\mathrm {d}}V\,.\end{array}}$

Der Kofaktor des Deformationsgradienten ist seine transponierte Adjunkte:

$\operatorname {cof}({\mathbf {F}}):=\operatorname {det}({\mathbf {F}}){\mathbf {F}}^{{\top -1}}\,.$

Es zeigt sich, dass die Hauptinvarianten des rechten Cauchy-Green Tensors Maße für die Änderung der Linien-, Flächen- und Volumenelemente sind:

${\begin{array}{rclclcc}\operatorname {I}_{1}({\mathbf {C}})&=&\operatorname {Sp}({\mathbf {C}})&=&\operatorname {Sp}({\mathbf {F^{\top }\cdot F}})={\mathbf {F}}:{\mathbf {F}}&=&\|{\mathbf {F}}\|^{2}\\\operatorname {I}_{2}({\mathbf {C}})&=&\operatorname {Sp(cof}({\mathbf {C}}))&=&\operatorname {Sp(cof}({\mathbf {F}})^{\top }\cdot \operatorname {cof}({\mathbf {F}}))&=&\|\operatorname {cof}({\mathbf {F}})\|^{2}\\\operatorname {I}_{3}({\mathbf {C}})&=&\operatorname {det}({\mathbf {C}})&=&\operatorname {det}({\mathbf {F^{\top }\cdot F}})&=&\operatorname {det}({\mathbf {F}})^{2}\end{array}}$

Die Frobeniusnorm $\|(\cdot )\|$ wird mit dem Frobenius-Skalarprodukt „:“ von Tensoren definiert:

$\mathbf {A} :\mathbf {B} :=\operatorname {Sp} (\mathbf {A^{\top }\cdot B} )\quad {\text{und}}\quad \|\mathbf {A} \|:={\sqrt {\mathbf {A} :\mathbf {A} }}\,.$

Physikalische Interpretation

Der Zusammenhang zwischen dem rechten Cauchy-Green Tensor und der Änderung der Linien-, Flächen- und Volumenelemente macht sich makroskopisch bemerkbar.

Sei

$\vec{x}=\vec{\chi}(\vec{X},t)$

die Bewegungsfunktion der Partikel eines materiellen Körpers. Die materiellen Koordinaten $\vec{X}$ nehmen die Partikel zu einer bestimmten Zeit $t_{0}$ ein, zu der der Körper in seiner undeformierten Ausgangslage vorliegt. Der zeitabhängige Vektor ${\vec {x}}$ bezeichnet die räumlichen Koordinaten, die die Partikel bei ihrer Bewegung – inklusive Deformation – zur Zeit t einnehmen.

Längen von Linien

Wenn im undeformierten Ausgangszustand eine materielle Linie ${\vec {X}}(s)$ mit dem Kurvenparameter $s\in [0,1]$ markiert wird, ergibt sich die Länge der Linie zu

$L=\int _{{0}}^{{1}}\left|{\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}\right|{\mathrm {d}}s=\int _{{0}}^{{1}}{\sqrt {{\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}\cdot {\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}}}{\mathrm {d}}s=\int _{{0}}^{{1}}{\sqrt {{\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}\cdot {\mathbf {I}}\cdot {\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}}}{\mathrm {d}}s\,.$

Darin ist $\mathbf {I}$ der Einheitstensor. In der deformierten Lage verändert sich diese Länge zu

$l=\int _{{0}}^{{1}}\left|{\frac {{\mathrm {d}}{\vec {\chi }}({\vec {X}}(s),t)}{{\mathrm {d}}s}}\right|{\mathrm {d}}s=\int _{{0}}^{{1}}{\sqrt {{\frac {{\mathrm {d}}{\vec {x}}}{{\mathrm {d}}s}}\cdot {\frac {{\mathrm {d}}{\vec {x}}}{{\mathrm {d}}s}}}}{\mathrm {d}}s=\int _{{0}}^{{1}}{\sqrt {\left({\mathbf {F}}\cdot {\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}\right)\cdot \left({\mathbf {F}}\cdot {\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}\right)}}{\mathrm {d}}s=\int _{{0}}^{{1}}{\sqrt {{\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}\cdot {\mathbf {C}}\cdot {\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}}}{\mathrm {d}}s\,.$

Die Änderung der Länge der markierten Linie wird also vom Strecktensor ${\mathbf {C}}$ bestimmt.

Flächeninhalte

Wenn in gleicher Weise im undeformierten Ausgangszustand eine materielle Fläche ${\vec {X}}(u,v)$ mit den Flächenparametern $(u,v)\in [0,1]^{2}$ bezeichnet wird, ergibt sich der Inhalt der Fläche zu

$F=\int _{0}^{1}\int _{0}^{1}{\biggl |}\overbrace {{\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} u}}\times {\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} v}}} ^{A{\vec {N}}}{\biggr |}\,\mathrm {d} u\mathrm {d} v=\int _{0}^{1}\int _{0}^{1}|{\vec {N}}|\,\overbrace {A\mathrm {d} u\mathrm {d} v} ^{\mathrm {d} A}=\int _{0}^{1}\int _{0}^{1}{\sqrt {{\vec {N}}\cdot \mathbf {I} \cdot {\vec {N}}}}\,\mathrm {d} A\,.$

In der deformierten Lage verändert sich diese Fläche zu

${\begin{array}{rcl}f&=&\displaystyle \int _{0}^{1}\int _{0}^{1}{\biggl |}\overbrace {{\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} u}}\times {\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} v}}} ^{a{\vec {n}}}{\biggr |}\,\mathrm {d} u\mathrm {d} v=\int _{0}^{1}\int _{0}^{1}|{\vec {n}}|\,\overbrace {a\mathrm {d} u\mathrm {d} v} ^{\mathrm {d} a}=\int _{0}^{1}\int _{0}^{1}|\operatorname {cof} (\mathbf {F} )\cdot {\vec {N}}|\,\mathrm {d} A\\&=&\displaystyle \int _{0}^{1}\int _{0}^{1}{\sqrt {{\vec {N}}\cdot \operatorname {cof} (\mathbf {F} )^{\top }\cdot \operatorname {cof} (\mathbf {F} )\cdot {\vec {N}}}}\,\mathrm {d} A=\int _{0}^{1}\int _{0}^{1}{\sqrt {{\vec {N}}\cdot \operatorname {cof} (\mathbf {C} )\cdot {\vec {N}}}}\,\mathrm {d} A\end{array}}$

Die Inhaltsänderung der markierten Fläche wird also vom Kofaktor des Strecktensors ${\mathbf {C}}$ bestimmt.

Volumina

Im undeformierten Ausgangszustand wird ein materielles Volumen ${\vec {X}}(\xi ,\eta ,\zeta )$ mit den Ortsparametern $(\xi ,\eta ,\zeta )\in [0,1]^{3}$ markiert. Das Volumen berechnet sich dann zu

$V=\int _{{0}}^{{1}}\int _{{0}}^{{1}}\int _{{0}}^{{1}}\overbrace {\operatorname {det}{\begin{pmatrix}{\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}\xi }}&{\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}\eta }}&{\frac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}\zeta }}\end{pmatrix}}\,{\mathrm {d}}\xi {\mathrm {d}}\eta {\mathrm {d}}\zeta }^{{{\mathrm {d}}V}}=\int _{{0}}^{{1}}\int _{{0}}^{{1}}\int _{{0}}^{{1}}{\sqrt {\operatorname {det}({\mathbf {I}})}}\,{\mathrm {d}}V$

In der deformierten Lage verändert sich dieses Volumen zu

${\begin{array}{rcl}v&=&\displaystyle \int _{0}^{1}\int _{0}^{1}\int _{0}^{1}\operatorname {det} {\begin{pmatrix}{\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} \xi }}&{\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} \eta }}&{\frac {\mathrm {d} {\vec {x}}}{\mathrm {d} \zeta }}\end{pmatrix}}\,\mathrm {d} \xi \mathrm {d} \eta \mathrm {d} \zeta =\int _{0}^{1}\int _{0}^{1}\int _{0}^{1}\operatorname {det} {\begin{pmatrix}\mathbf {F} \cdot {\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} \xi }}&\mathbf {F} \cdot {\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} \eta }}&\mathbf {F} \cdot {\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} \zeta }}\end{pmatrix}}\,\mathrm {d} \xi \mathrm {d} \eta \mathrm {d} \zeta \\&=&\displaystyle \int _{0}^{1}\int _{0}^{1}\int _{0}^{1}\operatorname {det} \left[\mathbf {F} \cdot {\begin{pmatrix}{\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} \xi }}&{\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} \eta }}&{\frac {\mathrm {d} {\vec {X}}}{\mathrm {d} \zeta }}\end{pmatrix}}\right]\,\mathrm {d} \xi \mathrm {d} \eta \mathrm {d} \zeta =\int _{0}^{1}\int _{0}^{1}\int _{0}^{1}\operatorname {det} (\mathbf {F} )\,\mathrm {d} V=\int _{0}^{1}\int _{0}^{1}\int _{0}^{1}{\sqrt {\operatorname {det} (\mathbf {C} )}}\,\mathrm {d} V\,,\end{array}}$

worin der Determinantenproduktsatz ausgenutzt wurde. Die Volumenänderung kann also wie bei den materiellen Linien und Flächen mit dem Strecktensor ausgedrückt werden.

Linker und rechter Strecktensor und Drehungen

Bei Nicht-Deformation sind die Strecktensoren gleich dem Einheitstensor und das unabhängig von eventuell auftretenden Drehungen des Körpers. Der Grund hierfür liegt in der Polarzerlegung des Deformationsgradienten

${\mathbf {F}}={\mathbf {R\cdot U}}={\mathbf {v\cdot R}}\,,$

die die Deformation lokal in eine Drehung, vermittelt durch den orthogonalen Rotationstensor $\mathbf{R}$ (mit ${\mathbf {R}}^{\top }={\mathbf {R}}^{{-1}}$ und der Determinante $\operatorname {det}({\mathbf {R}})=+1$ ), und eine reine Streckung, vermittelt durch die symmetrischen positiv definiten rechten bzw. linken Strecktensoren $\mathbf{U}$ bzw. $\mathbf {v}$ , aufspaltet. Durch die Multiplikation des Deformationsgradienten mit seiner transponierten heben sich die Drehungen $\mathbf{R}$ und "Rückdrehungen" ${\mathbf {R}}^{\top }={\mathbf {R}}^{{-1}}$ gegenseitig auf:

${\begin{array}{ccccccc}{\mathbf {F}}^{\top }\cdot {\mathbf {F}}&=&{\mathbf {U\cdot R}}^{\top }\cdot {\mathbf {R\cdot U}}&=&{\mathbf {U\cdot U}}&=&{\mathbf {C}}\\{\mathbf {F\cdot F}}^{\top }&=&{\mathbf {v\cdot R\cdot R}}^{\top }\cdot {\mathbf {v}}&=&{\mathbf {v\cdot v}}&=&{\mathbf {b}}\end{array}}$

was natürlich auch für die Inversen des rechten und linken Cauchy-Green-Tensors zutrifft. Der rechte und linke Cauchy-Green-Tensor und ihre Inversen sind daher von Drehungen des Körpers unbeeinflusst.

Hauptachsentransformationen

Der rechte und linke Strecktensor ebenso wie der rechte und linke Cauchy-Green-Tensor sind also ähnlich, weswegen sie dieselben Eigenwerte und daher auch dieselben Hauptinvarianten besitzen. Die Eigenwerte der Strecktensoren werden Hauptstreckungen genannt. Sämtliche Strecktensoren sind symmetrisch positiv definit und daher sind alle drei Eigenwerte positiv und die drei Eigenvektoren sind paarweise zueinander senkrecht (oder orthogonalisierbar), so dass sie eine Orthonormalbasis bilden. Seien ${\vec {N}}_{{1,2,3}}$ die Eigenvektoren von $\mathbf{U}$ , ${\vec {n}}_{{1,2,3}}$ die Eigenvektoren von $\mathbf {v}$ und $\lambda _{{1,2,3}}$ dessen Eigenwerte. Dann lauten die Hauptachsentransformationen:

${\mathbf {U}}=\sum _{{i=1}}^{{3}}\lambda _{{i}}{\vec {N}}_{{i}}\otimes {\vec {N}}_{{i}}\qquad {\textsf {und}}\qquad {\mathbf {v}}=\sum _{{i=1}}^{{3}}\lambda _{{i}}{\vec {n}}_{{i}}\otimes {\vec {n}}_{{i}}\,.$

Aus ${\mathbf {v}}={\mathbf {R}}\cdot {\mathbf {U}}\cdot {\mathbf {R}}^{\top }$ folgt:

${\mathbf {R}}\cdot {\vec {N}}_{{i}}={\vec {n}}_{{i}}\qquad {\text{also}}\qquad {\mathbf {R}}=\sum _{{i=1}}^{{3}}{\vec {n}}_{{i}}\otimes {\vec {N}}_{{i}}$

und weiter:

${\mathbf {F}}={\mathbf {R\cdot U}}={\mathbf {R}}\cdot \sum _{{i=1}}^{{3}}\lambda _{{i}}{\vec {N}}_{{i}}\otimes {\vec {N}}_{{i}}=\sum _{{i=1}}^{{3}}\lambda _{{i}}{\vec {n}}_{{i}}\otimes {\vec {N}}_{{i}}$

${\mathbf {C}}={\mathbf {U\cdot U}}=\sum _{{i=1}}^{{3}}\lambda _{i}^{{2}}{\vec {N}}_{{i}}\otimes {\vec {N}}_{{i}}$

${\mathbf {f}}={\mathbf {C}}^{{-1}}=\sum _{{i=1}}^{{3}}\lambda _{i}^{{-2}}{\vec {N}}_{{i}}\otimes {\vec {N}}_{{i}}$

${\mathbf {b}}={\mathbf {v\cdot v}}=\sum _{{i=1}}^{{3}}\lambda _{i}^{{2}}{\vec {n}}_{{i}}\otimes {\vec {n}}_{{i}}$

${\mathbf {c}}={\mathbf {b}}^{{-1}}=\sum _{{i=1}}^{{3}}\lambda _{i}^{{-2}}{\vec {n}}_{{i}}\otimes {\vec {n}}_{{i}}$

Ableitung der Streckungen

Manche Materialmodelle der Hyperelastizität beinhalten Funktionen der Eigenwerte $\lambda _{i}$ des linken Strecktensors $\mathbf {v}$ und die Spannungen ergeben sich aus der Ableitung dieser Funktionen nach dem linken Cauchy-Green-Tensor $\mathbf{b}$ . Deshalb lohnt es sich, die Ableitung der Eigenwerte $\lambda _{i}$ nach dem Strecktensor $\mathbf{b}$ bereitzustellen^[1]. Es ergibt sich

${\frac {\mathrm {d} \lambda _{i}}{\mathrm {d} \mathbf {b} }}={\frac {1}{2\lambda _{i}}}{\hat {n}}_{i}\otimes {\hat {n}}_{i}\,.$

Entsprechend berechnet sich

${\frac {\mathrm {d} \lambda _{i}}{\mathrm {d} \mathbf {C} }}={\frac {1}{2\lambda _{i}}}{\hat {N}}_{i}\otimes {\hat {N}}_{i}\,.$

Beweis

Betrachtet werden zunächst die Eigenwerte $\eta _{i}=\lambda _{i}^{2}$ des linken Cauchy-Green-Tensors. Die Eigenwerte $\eta _{i}$ lösen das charakteristische Polynom des linken Cauchy-Green-Tensors:

$\operatorname {det} (\mathbf {b} -\eta _{i}\operatorname {I} )=-\eta _{i}^{3}+\operatorname {I} _{1}\eta _{i}^{2}-\operatorname {I} _{2}\eta _{i}+\operatorname {I} _{3}=0\,.$
Die Koeffizienten dieses Polynoms sind die drei Hauptinvarianten des linken Cauchy-Green-Tensors. Implizite Differentiation des charakteristischen Polynoms unter Benutzung der Kettenregel und der Ableitungen der Hauptinvarianten bei symmetrischen Tensoren
${\frac {\mathrm {d} \operatorname {I} _{1}(\mathbf {b} )}{\mathrm {d} \mathbf {b} }}=\mathbf {I} ,\quad {\frac {\mathrm {d} \operatorname {I} _{2}(\mathbf {b} )}{\mathrm {d} \mathbf {b} }}=\operatorname {I} _{1}\mathbf {I} -\mathbf {b} \quad {\text{und}}\quad {\frac {\mathrm {d} \operatorname {I} _{3}(\mathbf {b} )}{\mathrm {d} \mathbf {b} }}=\operatorname {I} _{3}\mathbf {b} ^{-1}=\mathbf {b\cdot b} -\operatorname {I} _{1}\mathbf {b} +\operatorname {I} _{2}\mathbf {I}$
liefert
${\begin{aligned}0=&-3\eta _{i}^{2}{\frac {\mathrm {d} \eta _{i}}{\mathrm {d} \mathbf {b} }}+\eta _{i}^{2}\mathbf {I} +2\operatorname {I} _{1}\eta _{i}{\frac {\mathrm {d} \eta _{i}}{\mathrm {d} \mathbf {b} }}-(\operatorname {I} _{1}\mathbf {I} -\mathbf {b} )\eta _{i}-\operatorname {I} _{2}{\frac {\mathrm {d} \eta _{i}}{\mathrm {d} \mathbf {b} }}+\mathbf {b\cdot b} -\operatorname {I} _{1}\mathbf {b} +\operatorname {I} _{2}\mathbf {I} \\=&-(3\eta _{i}^{2}-2\operatorname {I} _{1}\eta _{i}+\operatorname {I} _{2}){\frac {\mathrm {d} \eta _{i}}{\mathrm {d} \mathbf {b} }}+(\eta _{i}^{2}-\eta _{i}\operatorname {I} _{1}+\operatorname {I} _{2})\mathbf {I} +(\eta _{i}-\operatorname {I} _{1})\mathbf {b} +\mathbf {b\cdot b} \\\rightarrow {\frac {\mathrm {d} \eta _{i}}{\mathrm {d} \mathbf {b} }}=&{\frac {(\eta _{i}^{2}-\eta _{i}\operatorname {I} _{1}+\operatorname {I} _{2})\mathbf {I} +(\eta _{i}-\operatorname {I} _{1})\mathbf {b} +\mathbf {b\cdot b} }{3\eta _{i}^{2}-2\operatorname {I} _{1}\eta _{i}+\operatorname {I} _{2}}}\end{aligned}}$
Einsetzen der Formeln von Vieta
$\operatorname {I} _{1}=\eta _{1}+\eta _{2}+\eta _{3}\quad {\text{und}}\quad \operatorname {I} _{2}=\eta _{1}\eta _{2}+\eta _{2}\eta _{3}+\eta _{3}\eta _{1}\,,$
der Hauptachsentransformation des linken Cauchy-Green-Tensors
$\mathbf {b} =\eta _{1}{\hat {n}}_{1}\otimes {\hat {n}}_{1}+\eta _{2}{\hat {n}}_{2}\otimes {\hat {n}}_{2}+\eta _{3}{\hat {n}}_{3}\otimes {\hat {n}}_{3}$
mit seinen auf Betrag eins normierten, paarweise orthogonalen Eigenvektoren ${\hat {n}}_{1,2,3}\,,$ die mit den Eigenvektoren des linken Strecktensors übereinstimmen, und der Form $\mathbf {I} ={\hat {n}}_{1}\otimes {\hat {n}}_{1}+{\hat {n}}_{2}\otimes {\hat {n}}_{2}+{\hat {n}}_{3}\otimes {\hat {n}}_{3}$ des Einheitstensors ergibt beispielsweise für i=1:
${\begin{aligned}{\frac {\mathrm {d} \eta _{1}}{\mathrm {d} \mathbf {b} }}=&{\frac {\eta _{1}^{2}-\eta _{1}(\eta _{1}+\eta _{2}+\eta _{3})+\eta _{1}\eta _{2}+\eta _{2}\eta _{3}+\eta _{3}\eta _{1}}{3\eta _{1}^{2}-2(\eta _{1}+\eta _{2}+\eta _{3})\eta _{1}+\eta _{1}\eta _{2}+\eta _{2}\eta _{3}+\eta _{3}\eta _{1}}}({\hat {n}}_{1}\otimes {\hat {n}}_{1}+{\hat {n}}_{2}\otimes {\hat {n}}_{2}+{\hat {n}}_{3}\otimes {\hat {n}}_{3})\\&+{\frac {[\eta _{1}-(\eta _{1}+\eta _{2}+\eta _{3})](\eta _{1}{\hat {n}}_{1}\otimes {\hat {n}}_{1}+\eta _{2}{\hat {n}}_{2}\otimes {\hat {n}}_{2}+\eta _{3}{\hat {n}}_{3}\otimes {\hat {n}}_{3})}{3\eta _{1}^{2}-2(\eta _{1}+\eta _{2}+\eta _{3})\eta _{1}+\eta _{1}\eta _{2}+\eta _{2}\eta _{3}+\eta _{3}\eta _{1}}}\\&+{\frac {\eta _{1}^{2}{\hat {n}}_{1}\otimes {\hat {n}}_{1}+\eta _{2}^{2}{\hat {n}}_{2}\otimes {\hat {n}}_{2}+\eta _{3}^{2}{\hat {n}}_{3}\otimes {\hat {n}}_{3}}{3\eta _{1}^{2}-2(\eta _{1}+\eta _{2}+\eta _{3})\eta _{1}+\eta _{1}\eta _{2}+\eta _{2}\eta _{3}+\eta _{3}\eta _{1}}}\\=&{\hat {n}}_{1}\otimes {\hat {n}}_{1}\end{aligned}}$
Für i=2 und i=3 berechnet sich entsprechendes, womit
${\frac {\mathrm {d} \eta _{i}}{\mathrm {d} \mathbf {b} }}={\hat {n}}_{i}\otimes {\hat {n}}_{i}$
feststeht. Die gesuchte Ableitung der Eigenwerte des linken Strecktensors nach dem linken-Cauchy-Green Tensor ermittelt sich schließlich aus
${\frac {\mathrm {d} \eta _{i}}{\mathrm {d} \mathbf {b} }}={\frac {\mathrm {d} \lambda _{i}^{2}}{\mathrm {d} \mathbf {b} }}=2\lambda _{i}{\frac {\mathrm {d} \lambda _{i}}{\mathrm {d} \mathbf {b} }}={\hat {n}}_{i}\otimes {\hat {n}}_{i}\quad \rightarrow \quad {\frac {\mathrm {d} \lambda _{i}}{\mathrm {d} \mathbf {b} }}={\frac {1}{2\lambda _{i}}}{\hat {n}}_{i}\otimes {\hat {n}}_{i}$

Beispiel

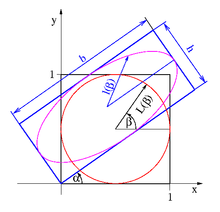
Ein Quadrat (schwarz) mit eingeschriebenem Kreis (rot) wird zu einem Rechteck (blau) mit eingeschriebener Ellipse (lila) verformt

Ein Quadrat der Seitenlänge eins wird zu einem Rechteck mit Breite und Höhe gestreckt und um einen Winkel $\alpha$ verdreht, siehe die Abbildung rechts. Das Quadrat sei im Ursprung eines kartesischen Koordinatensystems positioniert, so dass für die Punkte des Quadrates

${\vec {X}}=\left({\begin{array}{c}X\\Y\end{array}}\right)\in {[{0,1}]}^{{2}}$

gilt. Im deformierten Zustand ist dann

${\begin{array}{rcl}{\vec {x}}&=&\left({\begin{array}{c}x\\y\end{array}}\right)=\left({\begin{array}{cc}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{array}}\right)\left({\begin{array}{c}bX\\hY\end{array}}\right)\\&=&\left({\begin{array}{c}bX\cos \alpha -hY\sin \alpha \\bX\sin \alpha +hY\cos \alpha \end{array}}\right)\end{array}}\,.$

Damit berechnen sich der Deformationsgradient und die Strecktensoren zu

${\begin{array}{rcl}{\mathbf {F}}&=&\left({\begin{array}{cc}b\cos \alpha &-h\sin \alpha \\b\sin \alpha &h\cos \alpha \end{array}}\right)=\left({\begin{array}{cc}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{array}}\right)\left({\begin{array}{cc}b&0\\0&h\end{array}}\right)\\\rightarrow {\mathbf {R}}&=&\left({\begin{array}{cc}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{array}}\right)\\\rightarrow {\mathbf {U}}&=&\left({\begin{array}{cc}b&0\\0&h\end{array}}\right),\lambda _{{1}}=b,{\vec {N}}_{{1}}=\left({\begin{array}{c}1\\0\end{array}}\right),\lambda _{{2}}=h,{\vec {N}}_{{2}}=\left({\begin{array}{c}0\\1\end{array}}\right)\\\rightarrow {\mathbf {C}}&=&{\mathbf {U\cdot U}}=\left({\begin{array}{cc}b&0\\0&h\end{array}}\right)\left({\begin{array}{cc}b&0\\0&h\end{array}}\right)=\left({\begin{array}{cc}b^{{2}}&0\\0&h^{{2}}\end{array}}\right)={\mathbf {F}}^{\top }\cdot {\mathbf {F}}\\\rightarrow {\mathbf {v}}&=&b{\mathbf {R}}\cdot {\vec {N}}_{{1}}\otimes {\mathbf {R}}\cdot {\vec {N}}_{{1}}+h{\mathbf {R}}\cdot {\vec {N}}_{{2}}\otimes {\mathbf {R}}\cdot {\vec {N}}_{{2}}\\&=&b\left({\begin{array}{c}\cos \alpha \\\sin \alpha \end{array}}\right)\otimes \left({\begin{array}{c}\cos \alpha \\\sin \alpha \end{array}}\right)+h\left({\begin{array}{c}-\sin \alpha \\\cos \alpha \end{array}}\right)\otimes \left({\begin{array}{c}-\sin \alpha \\\cos \alpha \end{array}}\right)\\&=&\left({\begin{array}{cc}b{\cos }^{{2}}\alpha +h{\sin }^{{2}}\alpha &\left(b-h\right)\cos \alpha \sin \alpha \\\left(b-h\right)\sin \alpha \cos \alpha &b{\sin }^{{2}}\alpha +h{\cos }^{{2}}\alpha \end{array}}\right)\\&&\rightarrow \lambda _{{1}}=b,{\vec {n}}_{{1}}=\left({\begin{array}{c}\cos \alpha \\\sin \alpha \end{array}}\right),\lambda _{{2}}=h,{\vec {n}}_{{2}}=\left({\begin{array}{c}-\sin \alpha \\\cos \alpha \end{array}}\right)\\\rightarrow {\mathbf {b}}&=&{\mathbf {v\cdot v}}=\left({\begin{array}{cc}b^{{2}}{\cos }^{{2}}\alpha +h^{{2}}{\sin }^{{2}}\alpha &\left(b^{{2}}-h^{{2}}\right)\sin \alpha \cos \alpha \\\left(b^{{2}}-h^{{2}}\right)\sin \alpha \cos \alpha &b^{{2}}{\sin }^{{2}}\alpha +h^{{2}}{\cos }^{{2}}\alpha \end{array}}\right)={\mathbf {F\cdot F}}^{\top }\end{array}}$

In der Mitte des Quadrates wird eine gerade Linie der Länge ½ in einem Winkel $\beta$ zur x-Achse markiert, siehe Abbildung. Die Punkte auf der Linie haben in der Ausgangslage dann für $s\in [{0,1}]$ die Koordinaten:

${\begin{array}{rcl}{\vec {X}}\left(s\right)&=&{\dfrac {1}{2}}\left({\begin{array}{c}1+s\,\cos \beta \\1+s\,\sin \beta \end{array}}\right)\\\rightarrow {\dfrac {{\mathrm {d}}{\vec {X}}(s)}{{\mathrm {d}}s}}&=&{\dfrac {1}{2}}\left({\begin{array}{c}\cos \beta \\\sin \beta \end{array}}\right)\rightarrow \left|{\dfrac {{\mathrm {d}}{\vec {X}}\left(s\right)}{{\mathrm {d}}s}}\right|={\dfrac {1}{2}}\end{array}}$

Die Länge der Linie ist definitionsgemäß unabhängig von deren Richtung:

$L(\beta )=\int _{{0}}^{{1}}\left|{\dfrac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}\right|{\mathrm {d}}s=\int _{{0}}^{{1}}{\dfrac {1}{2}}{\mathrm {d}}s={\dfrac {1}{2}}\,.$

In der deformierten Lage haben die Punkte die Koordinaten

${\begin{array}{rcl}{\vec {x}}(s)&=&\left({\begin{array}{c}x\\y\end{array}}\right)={\dfrac {1}{2}}\left({\begin{array}{c}b(1+s\cos \beta )\cos \alpha -h(1+s\,\sin \beta )\sin \alpha \\b(1+s\,\cos \beta )\sin \alpha +h(1+s\,\sin \beta )\cos \alpha \end{array}}\right)\\\rightarrow {\dfrac {{\mathrm {d}}{\vec {x}}}{{\mathrm {d}}s}}&=&{\dfrac {1}{2}}\left({\begin{array}{c}b\cos \alpha \cos \beta -h\sin \alpha \sin \beta \\b\sin \alpha \cos \beta +h\cos \alpha \sin \beta \end{array}}\right)=\left({\begin{array}{cc}b\cos \alpha &-h\sin \alpha \\b\sin \alpha &h\cos \alpha \end{array}}\right){\dfrac {1}{2}}\left({\begin{array}{c}\cos \beta \\\sin \beta \end{array}}\right)={\mathbf {F}}\cdot {\dfrac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}\\\rightarrow \left|{\dfrac {{\mathrm {d}}{\vec {x}}}{{\mathrm {d}}s}}\right|&=&{\dfrac {1}{2}}{\sqrt {b^{{2}}{\cos }^{{2}}\beta +h^{{2}}{\sin }^{{2}}\beta }}\\&=&{\sqrt {{\dfrac {1}{2}}\left({\begin{array}{c}\cos \beta \\\sin \beta \end{array}}\right)\cdot \left({\begin{array}{cc}b^{{2}}&0\\0&h^{{2}}\end{array}}\right){\dfrac {1}{2}}\left({\begin{array}{c}\cos \beta \\\sin \beta \end{array}}\right)}}={\sqrt {{\dfrac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}\cdot {\mathbf {C}}\cdot {\dfrac {{\mathrm {d}}{\vec {X}}}{{\mathrm {d}}s}}}}\end{array}}$

Länge $l(\beta )$ der Linien im deformierten Quadrat in Abhängigkeit vom Winkel $\beta$ .

weswegen sich die Länge der Linie zu

${\begin{array}{rcl}l(\beta )&=&\displaystyle \int _{{0}}^{{1}}\left|{\dfrac {{\mathrm {d}}{\vec {x}}}{{\mathrm {d}}s}}\right|{\mathrm {d}}s=\int _{{0}}^{{1}}{\dfrac {1}{2}}{\sqrt {b^{{2}}{\cos }^{{2}}\beta +h^{{2}}{\sin }^{{2}}\beta }}{\mathrm {d}}s\\&=&{\dfrac {1}{2}}{\sqrt {b^{{2}}{\cos }^{{2}}\beta +h^{{2}}{\sin }^{{2}}\beta }}\end{array}}$

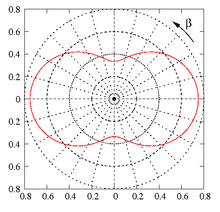
verändert. Das Ergebnis ist wiederum unabhängig vom Drehwinkel $\alpha$ . Bei Flächengleichheit des Quadrates und des Rechtecks ist

$b\cdot h=1\rightarrow h={\dfrac {1}{b}}$

und die Längen der deformierten Linie bilden in einem Polardiagramm eine Kurve wie in der Abbildung rechts. Dort ist b=1,5 .

Siehe auch

Mechanik:

Anmerkung

↑ Die Fréchet-Ableitung einer skalaren Funktion $f({\mathbf {T}})$ nach einem Tensor $\mathbf {T}$ ist der Tensor $\mathbf {A}$ für den - sofern er existiert - gilt:

${\mathbf {A}}:{\mathbf {H}}=\left.{\frac {{\mathrm {d}}}{{\mathrm {d}}s}}f({\mathbf {T}}+s{\mathbf {H}})\right|_{{s=0}}=\lim _{{s\rightarrow 0}}{\frac {f({\mathbf {T}}+s{\mathbf {H}})-f({\mathbf {T}})}{s}}\quad \forall \;{\mathbf {H}}$
Darin ist $s\in {\mathbb {R}}$ und ":" das Frobenius-Skalarprodukt. Dann wird auch

${\frac {\partial f}{\partial {\mathbf {T}}}}={\mathbf {A}}$
geschrieben.

Literatur

H. Altenbach: Kontinuumsmechanik. Springer, 2012, ISBN 978-3-642-24118-5.

Basierend auf Artikeln in:

Wikipedia.de