Abwickelbare Fläche

Eine abwickelbare Fläche bezeichnet aus der Anschauung heraus in der Geometrie bzw. in der Differentialgeometrie, der Kartografie und der Topologie eine zweidimensionale Fläche, die sich ohne innere Formverzerrung in die euklidische Ebene transformieren lässt. Es dürfen dabei endlich viele Schnitte gemacht werden, die Einzelteile müssen sich danach aber ohne weiteres Stauchen oder Quetschen glatt auf eine Ebene legen lassen.

Bekannteste Beispiele sind die Oberflächen bestimmter dreidimensionaler Körper wie Würfel oder Kegel. Die mathematische Definition läuft allgemeiner über die innere Metrik und Krümmung und ist unabhängig von einer möglichen Einbettung. Jedoch gilt für den Spezialfall des anschaulichen, dreidimensionalen, euklidischen Raumes mit induzierter Metrik, dass dort jede abwickelbare Fläche auch eine Regelfläche ist, obwohl Regelflächen ganz anders definiert werden. Die Umkehrung gilt nicht und ebenso wenig gilt die Aussage für Flächeneinbettungen in höherdimensionale euklidische Räume.

Eine abwickelbare Regelfläche nennt man auch Torse.

Definition

Eine Fläche oder genauer gesagt eine zwei-dimensionale differenzierbare Mannigfaltigkeit wird abwickelbar genannt, wenn ihre gaußsche Krümmung in jedem Punkt der Fläche gleich Null ist, was genau dann passiert, wenn eine der beiden (oder auch beide) Hauptkrümmungen gleich Null ist.

Eine riemannsche Mannigfaltigkeit der Dimension , deren riemannscher Krümmungstensor überall gleich Null ist, nennt man flache Mannigfaltigkeit. Also kann man eine abwickelbare Fläche auch als zwei-dimensionale flache Mannigfaltigkeit verstehen.

Beispiele

Abwickelbare Körper

Das Oloid ist einer der sehr wenigen bekannten Körper, dessen gesamte Oberfläche knickfrei und in einem Stück abwickelbar ist. Auch eckige Körper wie Prismen, Pyramiden oder Polyeder haben abwickelbare Oberflächen, die Kanten beeinflussen dies nicht: Eine geodätische Linie kann ohne „Knick“ über die Kante eines Prismas laufen und hat nach Ausbreitung in die Ebene einen geradlinigen Verlauf.

Mantelflächen

Beispiel für angenäherte Rotationskörper: Zwiebeltürme.
Hier: Obermillstatt in Kärnten mit einem Zwiebeldurchmesser von 8,5 m

Wichtige abwickelbare Mantelflächen sind u.a. die Oberflächen von Zylindern und Kegeln. Die darauf befindlichen Strukturen, Punkte, Koordinatenlinien usw. ändern ihre gegenseitige Lage nicht, wenn die Fläche in die Ebene „ausgebreitet“ wird. Diese Eigenschaft ist für die Kartografie und die Geodäsie wichtig, beispielsweise bei Kegelprojektionen oder der pseudo-zylindrischen Gauß-Krüger-Abbildung.

Das Merkmal der formtreuen Abwicklung gilt unabhängig vom Querschnitt der originalen Fläche, also z.B. auch für elliptische Zylinder.

Angenäherte Rotationskörper

Während sich einfache Rotationskörper wie Zylinder oder Kegel als Mantelfläche exakt abwickeln lassen, ist dies bei komplizierteren Rotationskörpern nicht mehr möglich. In der Praxis behilft man sich damit, den Körper aus einzelnen, abwickelbaren Segmenten zusammenzusetzen, die – anders als bei den Mantelflächen – nicht um die Rotationsachse herum, sondern längs zur Rotationsachse abgewickelt werden. Je größer die Anzahl der Segmente gewählt wird, desto besser nähert sich der zusammengesetzte Körper dem idealen Rotationskörper an.

Ein schönes Beispiel für solche angenäherten Rotationskörper sind Zwiebeltürme. Grundsätzlich lassen sich mit dieser Methode beliebige angenäherte Rotationskörper – auch Kugeln oder Ellipsoide – segmentweise abwickeln.

Nicht abwickelbare Flächen

Nicht abwickelbare Flächen sind solche, die in zwei Dimensionen gekrümmt sind, wie die Kugel, das Erdellipsoid oder verschiedene Sattelflächen. Hier kommt es bei jeder Abbildung auf eine Ebene (Landkarte, optische Abbildung usw.) zu kleinen oder größeren Formänderungen, den sog. Verzerrungen.

Technisches Zeichnen

Im technischen Zeichnen spricht man gleichbedeutend zur abwickelbaren Fläche von der Abwicklung (einer Fläche). Die Abwicklung ist dabei die zeichnerische Darstellung der abgewickelten Fläche, die beispielsweise bei der Fertigung von Blechrohren (z. B. Klempnerbedarf) zum Zuschnitt der Bleche benötigt wird (Blechabwicklung).

Auch wenn eckige bzw. kantige Körper in der Praxis eher selten für Abwicklungen verwendet werden, wird in der Ausbildung des technischen Zeichnens auch das eine oder andere Prisma oder die eine oder andere Pyramide abgewickelt dargestellt, um die Grundlagen der Konstruktion solcher Abwicklungen zu vermitteln.

Abwicklungen
Abwicklung eines Zylinders
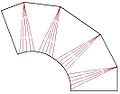Blechabwicklung
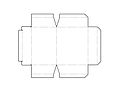Abwicklung eines Blechteils
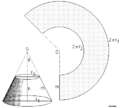Abgewickelter Kegelstumpf
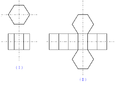Sechskantabwicklung

Weiteres

Längentreue; d. h. jeder Bogen geht in einen gleich langen über. Insbesondere gehen geodätische Linien in Geraden bzw. Geradenstücke über.
Die abwickelbaren Flächen (außer der Ebene) sind Einhüllende (Enveloppen) von einparametrigen Ebenenscharen.

Siehe auch

Abwicklung (Darstellende Geometrie)

Basierend auf einem Artikel in:

Wikipedia.de