Quadratische Menge

Der Begriff Quadratische Menge beschreibt in der synthetischen Geometrie Mengen, die in der analytischen Geometrie als projektive Quadriken bezeichnet werden, koordinatenfrei, allein durch Inzidenz- und Reichhaltigkeitseigenschaften. Er verallgemeinert diesen Begriff dabei so, dass er auch für nichtdesarguessche projektive Ebenen und für nicht-pappussche projektive Geometrien angewandt werden kann.^[1] Quadratische Mengen und ihre Tangentialräume sind selbst wieder Geometrien in einem allgemeineren Sinn, sogenannte Inzidenzstrukturen, in einigen Fällen sind sie sogar projektive Geometrien. Besonders nützlich ist der Begriff bei endlichen Geometrien.

Ellipsenzirkel nach Frans van Schooten. Der Gelenkmechanismus wurde von dem holländischen Mathematiker im 17. Jahrhundert erfunden. Wenn man am Stift in Punkt E zieht, zeichnet dieser eine Ellipse. Der Mechanismus ist an den Brennpunkten H und I auf der Zeichenunterlage befestigt. Die Konstruktion beruht auf der Definition der Ellipse als Ortslinie.

Geschichte

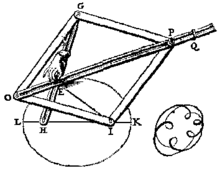
Quadriken in der Zeichenebene, insbesondere Ellipsen werden mindestens seit der klassischen Antike erforscht. Bis ins 18. Jahrhundert wurden sie durch Beschreibung ihrer Konstruktion mit Hilfe von Zeichengeräten (siehe die Abbildung am Ende der Einleitung) oder als Geometrischer Ort weitgehend ohne Bezug auf ein Koordinatensystem definiert. Man könnte daher für diese Zeit auch von einem „synthetischen“ Begriff der Quadriken sprechen. Allerdings wurde erst im 19. Jahrhundert eine axiomatische Grundlage für die projektive Geometrie entwickelt. Vorher hatte sie als geometrie descriptive nur aus Sprachregelungen für „uneigentliche“ Objekte bestanden, die der Zeichenebene oder dem Anschauungsraum „hinzugefügt“ werden. Seit der Jahrhundertwende zum 20. Jahrhundert sind nichtdesarguessche projektive Ebenen bekannt, bis in die 1960er Jahre wurden eine Vielzahl von (vor allem endlichen) Modellen für solche Ebenen gefunden. Die analytische Beschreibung von Quadriken als Nullstellenmenge von quadratischen Koordinatengleichungen, die für pappussche Geometrien zu einer befriedigenden algebraischen Klassifikation aller Quadriken geführt hat (siehe Hauptachsentransformation, Projektive Quadrik), lässt sich bereits für Geometrien über nichtkommutativen Schiefkörpern nur eingeschränkt verwenden, für nichtdesarguessche Ebenen ist sie weitgehend nutzlos. Der Begriff „Quadratische Menge“ wurde 1969 von Buekenhout eingeführt, um auch Quadriken in solchen Ebenen beschreiben zu können. Seit den 1970er Jahren werden Quadriken auf diese Weise systematisch untersucht. Da die endlichen projektiven Ebenen auch für die Kodierungstheorie eine wichtige Rolle spielen, werden in diesem Zusammenhang von Zeit zu Zeit Ergebnisse mit überraschenden Anwendungen scheinbar weitab der abstrakten Geometrie gefunden.

Definitionen

Ein (unbeschränkter) Doppelkegel im euklidischen Anschauungsraum ist in dessen projektivem Abschluss eine quadratische Menge und zählt zu den Kegeln. Diese quadratische Menge ist ausgeartet, denn der Tangentialraum der Spitze des Kegels ist der Gesamtraum, genauer besteht das Radikal des Kegels genau aus dieser Spitze. Schneidet man den Kegel mit einer Ebene, die die Spitze des Kegels nicht enthält, dann entsteht in dieser Ebene eine nichtausgeartete quadratische Menge. Die drei gezeigten Fälle Parabel (A), Ellipse (B) und Hyperbel (C) unterscheiden sich als quadratische Mengen im projektiven Abschluss der jeweiligen Schnittebene nur unwesentlich: Jede dieser quadratischen Mengen ist ein Oval. In Schnittebenen, die die Spitze des Kegels enthalten, wird auf die gleiche Weise eine der ausgearteten quadratischen Mengen Punkt, Gerade oder Doppelgerade induziert.

Quadratische Menge, Tangente

Sei $\mathbb{P}$ eine projektive Geometrie beliebiger, endlicher Dimension^[2] und sei ${\mathcal {Q}}$ eine Menge von Punkten dieser Geometrie.

Wenn eine Gerade der Geometrie entweder mit ${\mathcal {Q}}$ nur einen Punkt gemeinsam hat oder wenn jeder Punkt von in ${\mathcal {Q}}$ enthalten ist, dann heißt eine Tangente an ${\mathcal {Q}}$ .
Eine Tangente an ${\mathcal {Q}}$ , die mit ${\mathcal {Q}}$ nur einen Punkt gemeinsam hat, heißt eine Tangente an ${\mathcal {Q}}$ in .
Eine Tangente mit der Eigenschaft, dass jeder Punkt von in ${\mathcal {Q}}$ enthalten ist, heißt ${\mathcal {Q}}$ -Gerade, allgemeiner heißt ein Unterraum ein ${\mathcal {Q}}$ -Unterraum, falls jeder Punkt von in ${\mathcal {Q}}$ enthalten ist.
Für jeden Punkt $P\in {\mathcal {Q}}$ heißt die Menge ${\mathcal {Q}}_{P}$ , die aus dem Punkt und allen Punkten $A\neq P$ besteht, die mit durch eine Tangente verbunden sind, Tangentialraum von an ${\mathcal {Q}}$ . Dieser Tangentialraum wird auch als ${\mathfrak {T}}({\mathcal {Q}},P)$ notiert.

Die Menge ${\mathcal {Q}}$ heißt Quadratische Menge von $\mathbb{P}$ , falls die beiden folgenden Bedingungen erfüllt sind:

(„Wenn 3 dann alle!“) Jede Gerade , die mindestens drei Punkte von ${\mathcal {Q}}$ enthält, ist ganz in ${\mathcal {Q}}$ enthalten. Mit anderen Worten: Jede Gerade hat mit ${\mathcal {Q}}$ keinen, genau einen, genau zwei oder alle Punkte gemeinsam.
(Tangentenaxiom) Für jeden Punkt $P\in {\mathcal {Q}}$ ist der Tangentialraum ${\mathfrak {T}}({\mathcal {Q}},P)$ die Menge der Punkte einer Hyperebene oder die Menge aller Punkte von $\mathbb{P}$ .

Radikal, ausgeartete quadratische Menge

Für eine quadratische Menge ${\mathcal {Q}}$ ist ${\mathop {{\mathrm {Rad}}}}({\mathcal {Q}})$ die Menge aller Punkte $P\in {\mathcal {Q}}$ , für die ${\mathfrak {T}}({\mathcal {Q}},P)$ aus allen Punkten von $\mathbb{P}$ besteht. Diese Menge heißt das Radikal von ${\mathcal {Q}}$ .
Eine quadratische Menge heißt nichtausgeartet, falls ${\mathop {{\mathrm {Rad}}}}({\mathcal {Q}})=\emptyset$ ist, sonst heißt sie ausgeartet.

Index einer quadratischen Menge

Es sei ${\mathcal {Q}}$ eine quadratische Menge, die größte Dimension eines ${\mathcal {Q}}$ -Unterraums. Dann heißt der Index von ${\mathcal {Q}}$ . Man nennt die ${\mathcal {Q}}$ -Unterräume der Dimension dann auch maximale ${\mathcal {Q}}$ -Unterräume.

Oval und Ovoid

→ Hauptartikel: Oval (Projektive Geometrie)

→ Hauptartikel: Ovoid (Projektive Geometrie)

Eine nichtleere Punktmenge ${\mathcal {O}}$ in einer projektiven Ebene $\mathbb{P}$ heißt ein Oval, falls keine drei Punkte von ${\mathcal {O}}$ kollinear sind und durch jeden Punkt von ${\mathcal {O}}$ genau eine Tangente geht.^[3]

Die Verallgemeinerung des Ovals für beliebigdimensionale Räume ist das Ovoid:

Eine nichtleere Punktmenge ${\mathcal {O}}$ in einem -dimensionalen Raum $\mathbb{P}$ heißt Ovoid, falls gilt:

Keine drei Punkte von ${\mathcal {O}}$ sind kollinear,
für jeden Punkt $P\in {\mathcal {O}}$ ist ${\mathfrak {T}}({\mathcal {Q}},P)$ eine Hyperebene.^[3]

Nukleus und Hyperoval

Im Falle seiner Existenz heißt der gemeinsame Schnittpunkt aller Tangenten an ein Oval in einer endlichen Ebene der Nukleus des Ovals.
Die Menge der Punkte, die aus einem Oval zusammen mit seinem Nukleus. besteht, wird als Hyperoval bezeichnet.

Kegel

Sei eine Hyperebene des projektiven Raumes $\mathbb{P}$ , ein Punkt, der nicht in liegt und ${\mathcal {Q}}^{*}$ eine nichtausgeartete, nichtleere quadratische Menge von . Dann heißt die quadratische Menge

${\mathcal {Q}}:=\bigcup _{{X\in {\mathcal {Q}}^{*}}}(SX)$

ein Kegel mit Spitze über ${\mathcal {Q}}^{*}$ .

Elliptische, parabolische und hyperbolische quadratische Mengen

Sei ${\mathcal {Q}}$ eine nichtausgeartete quadratische Menge in einer -dimensionalen projektiven Geometrie $\mathbb{P}$ . Dann werden folgende Bezeichnungen vereinbart:

Haupttypen von quadratischen Mengen, klassifiziert nach ihrem Index
Raumdimension d	Index t	Bezeichnung der quadratischen Menge
ist gerade	$t={\frac {d}{2}}$	parabolisch
ist ungerade	$t={\frac {d-1}{2}}$	elliptisch
ist ungerade	$t={\frac {d+1}{2}}$	hyperbolisch

Eigenschaften

Index

Es sei ${\mathcal {Q}}$ eine quadratische Menge vom Index in einer -dimensionalen projektiven Geometrie $\mathbb{P}$ .

Dann geht durch jeden Punkt von ${\mathcal {Q}}$ ein maximaler ${\mathcal {Q}}$ -Unterraum.

Genauer gilt: Durch jeden Punkt von ${\mathcal {Q}}$ außerhalb eines -dimensionalen Unterraumes gibt es einen -dimensionalen ${\mathcal {Q}}$ -Unterraum , der in einem -dimensionalen Unterraum schneidet.

Ist die quadratische Menge nichtausgeartet und nichtleer, dann

ist $t\leq {\frac {d}{2}}$ , falls gerade ist und
$t\leq {\frac {d+1}{2}}$ , falls ungerade ist.

Ist darüber hinaus $\mathbb{P}$ endlich, dann

ist $t={\frac {d}{2}}$ , falls gerade ist und
$t\in \lbrace {\frac {d-1}{2}},{\frac {d+1}{2}}\rbrace$ , falls ungerade ist.

Mit anderen Worten: In einer endlichen projektiven Geometrie ist jede nichtausgeartete und nichtleere quadratische Menge

parabolisch, falls die Dimension gerade ist,
elliptisch oder hyperbolisch, falls ungerade ist.

Klassifikation quadratischer Mengen in der Ebene

Sei ${\mathcal {Q}}$ eine quadratische Menge in einer projektiven Ebene $\mathbb{P}$ . Dann ist ${\mathcal {Q}}$ die leere Menge, eine einpunktige Menge, die Punktmenge einer oder zweier Geraden, die gesamte Punktmenge oder ein Oval. Genau dann, wenn die quadratische Menge ${\mathcal {Q}}$ nichtleer und nichtausgeartet ist, ist sie ein Oval.

Satz von Segre, quadratische Mengen und Quadriken in pappusschen Räumen

Es sei ${\mathbb {P}}={\mathbb {P}}(K^{{d+1}})$ der d-dimensionale, pappussche projektive Raum über einem Körper K, dessen Charakteristik nicht 2 sei. Dann gilt:

Jede projektive Quadrik von $\mathbb{P}$ ist eine quadratische Menge. Eine Quadrik ist genau dann als quadratische Menge nichtausgeartet, wenn die zugehörige quadratische Form nichtausgeartet ist.
Ist und ein endlicher Körper, dann ist jede quadratische Menge eine projektive Quadrik.

Die zweite Aussage folgt aus dem Satz von Segre:

Jedes Oval in einer endlichen desarguesschen Ebene ungerader Ordnung ist ein Kegelschnitt (im Sinne der analytischen Geometrie).

In den endlichen Ebenen gerader Ordnung existieren im Allgemeinen Ovale, die keine projektiven Quadriken sind. Genauer gilt:
1. In den desarguesschen endlichen Ebenen und ist jedes Oval eine projektive Quadrik.
2. In jeder desarguesschen endlichen Ebene $P(2,2^{r})$ gerader Ordnung mit $r\geq 3$ existieren Ovale, die keine projektiven Quadriken sind. Jedes solche Oval entsteht aus einem Oval ${\mathcal {Q}}$ , das eine projektive Quadrik ist, indem ein beliebiger Punkt der Quadrik ${\mathcal {Q}}$ durch den Nukleus dieses Ovals ${\mathcal {Q}}$ ersetzt wird.

Parabolische quadratische Menge

Sei ${\mathcal {Q}}$ eine parabolische quadratische Menge in einem 2-dimensionalen projektiven Raum $(t\geq 2)$ . Dann gilt:

Ist eine Tangentialhyperebene von ${\mathcal {Q}}$ , dann ist die in induzierte Quadrik ${\mathcal {Q}}^{*}={\mathcal {Q}}\cap H$ ein Kegel über einer parabolischen quadratischen Menge.
Ist eine Hyperebene, die keine Tangentialhyperebene von ${\mathcal {Q}}$ ist, dann ist die in induzierte Quadrik ${\mathcal {Q}}^{*}={\mathcal {Q}}\cap H$ eine elliptische oder hyperbolische quadratische Menge.

Hyperbolische quadratische Menge

Sei ${\mathcal {Q}}$ eine hyperbolische quadratische Menge in einem 2t+1 -dimensionalen projektiven Raum $(t\geq 2)$ .

Ist eine Tangentialhyperebene von ${\mathcal {Q}}$ , dann ist die in induzierte Quadrik ${\mathcal {Q}}^{*}={\mathcal {Q}}\cap H$ ein Kegel über einer hyperbolischen quadratischen Menge.
Ist eine Hyperebene, die keine Tangentialhyperebene von ${\mathcal {Q}}$ ist, dann ist die in induzierte Quadrik ${\mathcal {Q}}^{*}={\mathcal {Q}}\cap H$ eine parabolische quadratische Menge.

Wenn in einem mindestens dreidimensionalen projektiven Raum eine hyperbolische quadratische Menge existiert, dann ist der Raum pappossch, also über einem kommutativen Körper koordinatisiert.

Anzahlen in endlichen Räumen

Es sei ${\mathcal {Q}}$ eine quadratische Menge in einer -dimensionalen projektiven Geometrie ${\mathbb {P}}={\mathbb {P}}({{\mathbb {F}}_{q}}^{{d+1}})$ über dem endlichen Körper $\mathbb {F} _{q}$ . Für einen beliebigen Punkt $P\in {\mathcal {Q}}\setminus {\mathop {{\mathrm {Rad}}}}({\mathcal {Q}})$ sei $a_{P}$ die Anzahl der ${\mathcal {Q}}$ -Geraden durch . Dann gilt:

Die Anzahl $a=a_{P}$ ist unabhängig von der Wahl von $P\in {\mathcal {Q}}\setminus {\mathop {{\mathrm {Rad}}}}({\mathcal {Q}}).$
Ist $H={\mathfrak {T}}({\mathcal {Q}},P)$ eine Hyperebene, was für $P\in {\mathcal {Q}}\setminus {\mathop {{\mathrm {Rad}}}}({\mathcal {Q}})$ stets der Fall ist, dann enthält genau Punkte von ${\mathcal {Q}}.$
Die quadratische Menge ${\mathcal {Q}}$ enthält genau $1+q^{{d-1}}+aq$ Punkte.

Beispiele

Ein Eirund in der reellen Ebene ist ein Oval und eine quadratische Menge im Sinne der synthetischen Definition, aber im Allgemeinen keine Quadrik!

Die leere Menge ist in jeder projektiven Geometrie eine nichtausgeartete quadratische Menge. In einem mindestens eindimensionalen projektiven Raum über den komplexen Zahlen $\mathbb {P} (\mathbb {C} ^{d+1}),d\geq 1$ ist sie keine projektive Quadrik.
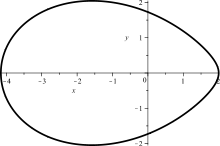
Ovale und Ovoide im herkömmlichen Sinn in reellen affinen Räumen, wie zum Beispiel das „Eirund“ in der Abbildung rechts sind im projektiven Abschluss des Raumes immer quadratische Mengen.

Index

In zwei- bzw. dreidimensionalen Räumen treten die folgenden nichtausgearteten, nichtleeren, quadratischen Mengen ${\mathcal {Q}}$ , die Quadriken sind, auf:

In zweidimensionalen Räumen hat ${\mathcal {Q}}$ stets den Index 1 und ist ein parabolisches Oval, das heißt die maximale Dimension enthaltener Teilräume ist 0, Einzelpunkte sind die größten enthaltenen Teilräume. In der affinen Klassifikation unterscheidet man 3 Typen: Ellipse, Parabel und Hyperbel, diese sind aber im projektiven Abschluss äquivalent.
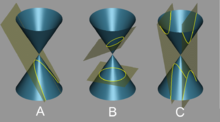
In dreidimensionalen Räumen hat den Index 1 oder 2.
- Beim Index 1 ist ${\mathcal {Q}}$ elliptisch. Es handelt sich dann in der affinen Klassifikation um ein Ellipsoid, ein Paraboloid oder um ein zweischaliges Hyperboloid, die jeweils wieder projektiv äquivalent sind.
- Beim Index 2 ist ${\mathcal {Q}}$ hyperbolisch: Es handelt sich in der affinen Klassifikation um ein einschaliges Hyperboloid. Durch jeden Punkt von ${\mathcal {Q}}$ – und dies gilt auch im projektiven Abschluss – gehen genau zwei ${\mathcal {Q}}$ -Geraden. Die Gesamtheit aller ${\mathcal {Q}}$ -Geraden zerfällt in zwei Scharen, deren jede die Fläche ${\mathcal {Q}}$ als Regelfläche erzeugt.

Lösungsanzahlen für homogene quadratische Gleichungen

Die Gleichung $Q:A_{1}x_{1}^{2}+A_{2}x_{2}^{2}+A_{3}x_{3}^{2}=0;A_{1},A_{2},A_{3}\in K^{*}$ beschreibt in jeder projektiven Ebene über einem Körper eine projektive Quadrik, also eine quadratische Menge ${\mathcal {Q}}=\{\langle (x_{1},x_{2},x_{3})\rangle \in {\mathbb {P}}(K^{3})|A_{1}x_{1}^{2}+A_{2}x_{2}^{2}+A_{3}x_{3}^{2}=0\}$ . Diese ist – sofern die Charakteristik von nicht 2 ist – nie ausgeartet.

Ist $K={\mathbb {F}}_{q}$ der endliche Körper mit q Elementen (q ungerade), dann gilt:

Die Gleichung besitzt eine nichttriviale Lösung, die quadratische Menge ${\mathcal {Q}}$ hat den Index 1 und ist also ein Oval.
${\mathcal {Q}}$ enthält genau projektive Punkte, drei verschiedene Punkte in ${\mathcal {Q}}$ sind nie kollinear.
Die Gleichung hat genau $(q-1)(q+1)=q^{2}-1$ nichttriviale Lösungen.

Fano-Ebene

Koordinatisiertes Modell der Fano-Ebene. Die Ecken des äußeren, gleichschenkligen Dreiecks

bilden eine quadratische Menge: Ein Oval. Zusammen mit dem Punkt

bilden diese Punkte ein vierpunktiges Hyperoval.

In der Fano-Ebene, der projektiven Ebene über dem Körper mit 2 Elementen $K=\mathbb{Z } /2\mathbb{Z }$ , ist die Nullstellenmenge der Quadrik $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=0$ gleich der Nullstellenmenge der Geradengleichung $x_{1}+x_{2}+x_{3}=0$ . Die zugehörige quadratische Menge ist also eine Gerade und wie die Quadriken $x_{1}^{2}+x_{2}^{2}=0$ und $x_{1}^{2}=0$ , die ebenfalls Geraden beschreiben, ausgeartet.

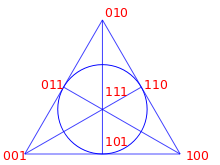
Dagegen ist $x_{1}x_{2}+x_{2}x_{3}+x_{3}x_{1}=0$ eine nicht zu den genannten äquivalente Quadrik. Ihre Erfüllungsmenge besteht genau aus den projektiven Punkten, für die genau eine Koordinate ungleich 0 ist, vergleiche die Abbildung, die quadratische Menge ist ein Oval. Der Mittelpunkt des Dreiecks im Modell ist der Schnittpunkt aller drei Tangenten, also bilden die Ecken zusammen mit dem Mittelpunkt ein Hyperoval. Alle Ovale und Hyperovale in der Fano-Ebene gehen durch eine Projektivität aus diesem Oval bzw. Hyperoval hervor. Hyperovale sind genau die Komplemente der sieben Geraden, das sind alle vollständigen Vierecke der Fano-Ebene. Lässt man aus einem solchen Hyperoval einen beliebigen Punkt fort, so erhält man ein neues, zu dem dargestellten äquivalentes Oval.

Literatur

Albrecht Beutelspacher, Ute Rosenbaum: Projektive Geometrie. Von den Grundlagen bis zu den Anwendungen (= Vieweg Studium: Aufbaukurs Mathematik). 2., durchgesehene und erweiterte Auflage. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X.

Anmerkungen

↑ Tatsächlich ist der Begriff „quadratische Menge“ in vielen Fällen echt umfassender als „projektive Quadrik“ und damit nicht gleichwertig zu diesem analytischen Begriff. Gleichwertig sind die Begriffe in endlichen, desarguesschen Fano-Ebenen, beachte dazu die Beispiele im vorliegenden Artikel.
↑ $\mathbb{P}$ ist in diesem Artikel durchgehend eine solche Geometrie.
↑ ^{a
b} Aus der Definition folgt, dass ein Oval bzw. Ovoid eine nichtausgeartete quadratische Menge der Ebene bzw. des Raumes ist.

Basierend auf einem Artikel in:

Wikipedia.de