Satz von Segre (Projektive Geometrie)

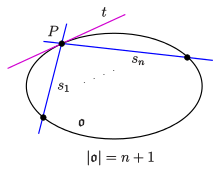
Zur Definition eines endlichen Ovals:

Tangente, $s_{1},...s_{n}$ Sekanten, ist die Ordnung der projektiven Ebene (Anzahl der Punkte auf einer Gerade −1)

Der Satz von Segre, benannt nach dem italienischen Mathematiker Beniamino Segre, ist in der projektiven Geometrie die Aussage:

In einer endlichen pappusschen projektiven Ebene ungerader Ordnung ist jedes Oval ein Kegelschnitt.

Die Aussage wurde 1949 von den finnischen Mathematikern G. Järnefelt und P. Kustaanheimo vermutet und ihr Beweis 1955 von B. Segre publiziert.

Eine endliche pappussche projektive Ebene kann man sich in inhomogenen Koordinaten wie die reelle projektive Ebene beschrieben denken, nur dass man statt der reellen Zahlen einen endlichen Körper benutzt. Ungerader Ordnung bedeutet, dass $|K|=n$ ungerade ist. Ein Oval ist eine kreisähnliche Kurve (s.u.): Eine Gerade schneidet höchstens 2-mal und in jedem Punkt gibt es genau eine Tangente. Die Standardbeispiele von Ovalen sind die nicht ausgearteten (projektiven) Kegelschnitte.

Der Satz von Segre hat für endliche Ovale eine sehr große Bedeutung, da es im pappusschen ungeraden Fall außer den Kegelschnitten keine weiteren Ovale geben kann. Im Gegensatz zu geraden pappussche Ebenen: Hier gibt es Ovale, die keine Kegelschnitte sind (s. Satz von Qvist). In unendlichen pappusschen Ebenen gibt es Ovale, die keine Kegelschnitte sind. Im Reellen muss man nur einen Halbkreis glatt mit einer geeigneten Halbellipse zusammensetzen.

Der Beweis des Satzes für den Nachweis, dass das gegebene Oval ein Kegelschnitt ist, wird mit Hilfe der 3-Punkte-Ausartung des Satzes von Pascal geführt. Dabei wird die für Körper ungerader Ordnung typische Eigenschaft, dass das Produkt aller Elemente, die nicht 0 sind, gleich −1 ist, verwendet.

Definition eines Ovals

→ Hauptartikel: Oval (Projektive Geometrie)

Eine Menge ${\mathfrak {o}}$ von Punkten in einer projektiven Ebene heißt Oval, wenn

(1) Eine beliebige Gerade trifft ${\mathfrak {o}}$ in höchstens 2 Punkten.
Falls $|g\cap {\mathfrak {o}}|=0$ ist, heißt Passante, falls $|g\cap {\mathfrak {o}}|=1$ ist, heißt Tangente und falls $|g\cap {\mathfrak {o}}|=2$ ist, heißt Sekante.

(2) Zu jedem Punkt $P\in {\mathfrak {o}}$ gibt es genau eine Tangente

, d.h. $t\cap {\mathfrak {o}}=\{P\}$ .

Für endliche projektive Ebenen (d.h. die Punktmenge und Geradenmenge sind endlich) gilt

In einer projektiven Ebene der Ordnung (d.h. jede Gerade enthält $n+1$ Punkte) ist eine Menge ${\mathfrak {o}}$ genau dann ein Oval, wenn $|{\mathfrak {o}}|=n+1$ ist und keine drei Punkte von ${\mathfrak {o}}$ kollinear (auf einer Gerade) liegen.

3-Punkte-Ausartung des Satzes von Pascal

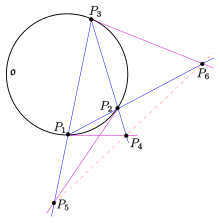
für den Beweis ist $g_{\infty }$ die Tangente in $P_{3}$

Satz:

Es sei ${\mathfrak {o}}$ ein Oval in einer pappusschen projektiven Ebene der Charakteristik $\neq 2$ .
${\mathfrak {o}}$ ist genau dann ein nicht ausgearteter Kegelschnitt, falls die folgende Aussage (P3) gilt:

(P3): Ist P_1,P_2,P_3

ein beliebiges Dreieck auf ${\mathfrak {o}}$ und ist ${\overline {P_{i}P_{i}}}$ die Tangente in $P_{i}$ an ${\mathfrak {o}}$ , so sind die Punkte

$P_{4}:={\overline {P_{1}P_{1}}}\cap {\overline {P_{2}P_{3}}},\ P_{5}:={\overline {P_{2}P_{2}}}\cap {\overline {P_{1}P_{3}}},\ P_{6}:={\overline {P_{3}P_{3}}}\cap {\overline {P_{1}P_{2}}}$

kollinear.

Zum Beweis des 3P-Pascal-Satzes

Beweis:

Die projektive Ebene werde in inhomogenen Koordinaten über dem Körper so dargestellt, dass $P_{3}=(0),\;g_{\infty }$ die Tangente in $P_{3},\ (0,0)\in {\mathfrak {o}}$ , die x-Achse die Tangente im Punkt (0,0) ist und ${\mathfrak {o}}$ den Punkt (1,1) enthält. Ferner sei $P_{1}=(x_{1},y_{1}),\;P_{2}=(x_{2},y_{2})\ .$ (s. Bild)
Das Oval ${\mathfrak {o}}$ lässt sich mit Hilfe einer Funktion $f:K\mapsto K$ so beschreiben:

${\mathfrak {o}}=\{(x,y)\in K^{2}\;|\;y=f(x)\}\ \cup \{(\infty )\}\;.$

Die Tangente im Punkt $(x_{0},f(x_{0}))$ werde mit Hilfe einer Funktion durch die Gleichung

$y=f'(x_{0})(x-x_{0})+f(x_{0})$

beschrieben. Es gilt dann (s. Bild)

$P_{5}=(x_{1},f'(x_{2})(x_{1}-x_{2})+f(x_{2}))\;$ und $P_{4}=(x_{2},f'(x_{1})(x_{2}-x_{1})+f(x_{1}))\;.$

I: Falls ${\mathfrak {o}}$ ein nicht ausgearteter Kegelschnitt ist, ist $f(x)=x^{2}$ und f'(x)=2x und man rechnet leicht nach, dass $P_{4},P_{5},P_{6}$ kollinear sind (siehe Parabel).

II: Falls ${\mathfrak {o}}$ ein Oval mit der Eigenschaft (P3) ist, ist die Steigung der Gerade ${\overline {P_{4}P_{5}}}$ gleich der Steigung der Gerade $\overline {P_{1}P_{2}}$ , d.h. es ist

$f'(x_{2})+f'(x_{1})-{\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}={\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}$ und damit gilt

(i): $(f'(x_{2})+f'(x_{1}))(x_{2}-x_{1})=2(f(x_{2})-f(x_{1}))$ für alle $x_{1},x_{2}\in K$ .

Mit $f(0)=f'(0)=0$ erhält man

(ii): $f'(x_{2})x_{2}=2f(x_{2})$ und mit f(1)=1

folgt

(iii): $f'(1)=2\;.$

Aus (i) und (ii) ergibt sich

(iv): $f'(x_{2})x_{1}=f'(x_{1})x_{2}$ und mit (iii) schließlich

(v): $f'(x_{2})=2x_{2}$ für alle $x_{2}\in K$ .

Aus (ii) und (v) folgt

$f(x_{2})=x_{2}^{2},\;x_{2}\in K$ .

Also ist ${\mathfrak {o}}$ ein nicht ausgearteter Kegelschnitt.

Bemerkung:

Die Eigenschaft (P3) ist in pappusschen Ebenen der Charakteristik 2 für alle Ovale mit einem Knoten N (alle Geraden durch N sind Tangenten) erfüllt. Also auch für Ovale, die keine Kegelschnitte sind.
Der 3-Punkte-Pascal-Satz ist auch für Ovale in unendlichen pappusschen Ebenen über Körper der Charakteristik $\neq 2$ gültig.

Aussage und Beweis des Satzes von Segre

Satz:

Ein Oval ${\mathfrak {o}}$ in einer endlichen pappusschen projektiven Ebene ungerader Ordnung ist ein nicht ausgearteter Kegelschnitt.

3-Punkte-Ausartung des Satzes von Pascal, für den Beweis ist $g_{\infty }={\overline {P_{2}P_{3}}}$

Satz von Segre: zum Beweis

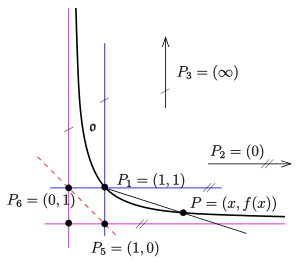
Beweis:

Zum Beweis wird nachgewiesen, dass das Oval die Eigenschaft (P3) der 3-Punkte-Ausartung des Satzes von Pascal (s.o.) erfüllt.

Sei also P_1,P_2,P_3 ein beliebiges Dreieck auf ${\mathfrak {o}}$ und $P_{4},P_{5},P_{6}$ wie in (P3) erklärt. Die pappussche Ebene wird so in inhomogenen Koordinaten über einem endlichen Körper dargestellt, dass $P_{3}=(\infty ),\;P_{2}=(0),\;P_{1}=(1,1)$ und $(0,0)$ der Schnittpunkt der Tangenten in $P_{2}$ und $P_{3}$ ist. Das Oval ${\mathfrak {o}}$ lässt sich mit Hilfe einer bijektiven Funktion $f:K^{*}:=K\cup \setminus \{0\}\mapsto K^{*}$ darstellen:

${\mathfrak {o}}=\{(x,y)\in K^{2}\;|\;y=f(x),\;x\neq 0\}\;\cup \;\{(0),(\infty )\}\;.$

Ist nun $P=(x,y),\;x\in K\setminus \{0,1\}$ , so ist $m(x)={\tfrac {f(x)-1}{x-1}}$ die Steigung der Sekante ${\overline {PP_{1}}}\;.$ Da sowohl $x\mapsto f(x)-1$ als auch $x\mapsto x-1$ eine Bijektion von $K\setminus\{0,1\}$ auf $K\setminus \{0,-1\}$ ist, und $x\mapsto m(x)$ eine Bijektion von $K\setminus\{0,1\}$ auf $K\setminus \{0,m_{1}\}$ ist, wobei $m_{1}$ die Steigung der Tangente in $P_{1}$ ist, gilt für $K^{**}:=K\setminus \{0,1\}\;:$

$\prod _{x\in K^{**}}(f(x)-1)=\prod _{x\in K^{**}}(x-1)=1\quad {\text{und}}\quad m_{1}\cdot \prod _{x\in K^{**}}{\frac {f(x)-1}{x-1}}=-1\;.$

(Man beachte: Für $K^{*}:=K\setminus \{0\}$ gilt: $\displaystyle \prod _{k\in K^{*}}k=-1\;.$ )
Also ist

$-1=m_{1}\cdot \prod _{x\in K^{**}}{\frac {f(x)-1}{x-1}}=m_{1}\cdot {\frac {\displaystyle \prod _{x\in K^{**}}(f(x)-1)}{\displaystyle \prod _{x\in K^{**}}(x-1)}}=m_{1}\;.$

Da die Steigungen von ${\overline {P_{5}P_{6}}}$ und der Tangente ${\overline {P_{1}P_{1}}}$ beide sind, ergibt sich ${\overline {P_{1}P_{1}}}\cap {\overline {P_{2}P_{3}}}=P_{4}\in {\overline {P_{5}P_{6}}}$ . Dies gilt für jedes Dreieck $P_{1},P_{2},P_{3}\in {\mathfrak {o}}$ .

Also gilt die Eigenschaft (P3) der 3-Punkte-Ausartung des Satzes von Pascal und das Oval ist ein nicht ausgearteter Kegelschnitt.

Literatur

Albrecht Beutelspacher, Ute Rosenbaum: Projektive Geometrie. 2. Auflage. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X.

Basierend auf einem Artikel in:

Wikipedia.de