Kegel (Topologie)

In dem mathematischen Teilgebiet der Topologie ist ein Kegel über einem Raum eine bestimmte aus diesem konstruierte Punktmenge, die in natürlicher Weise selbst wieder einen topologischen Raum bildet. Im euklidischen Fall ist dieser tatsächlich homöomorph zu einem geometrischen Kegel, im Allgemeinen ist die topologische Definition jedoch umfassender. Hauptsächlich werden Kegel über topologischen Räumen in der algebraischen Topologie betrachtet.

Definition

Kegel über einem Kreis. Der ursprüngliche Raum ist blau, der zusammengeschlagene Endpunkt grün gefärbt.

Sei ein topologischer Raum. Der Kegel über ist definiert als die Menge

$CX:=(X\times [0;1])/(X\times \{1\})$

versehen mit der Quotiententopologie bezüglich der kanonischen Projektion.

Die Bezeichnung stammt dabei vom lateinischen Wort conus für Kegel.

Ausführlich bedeutet das:

Es seien ein topologischer Raum und $[0;1]\subset \mathbb{R}$ das reelle Einheitsintervall mit der Teilraumtopologie. Sei weiter auf dem Produkt $X\times [0;1]$ dieser beiden Räume durch

$x\sim y:\Leftrightarrow x=y\lor x,y\in (X\times \{1\})$

eine Äquivalenzrelation erklärt. Setze nun

$CX=(X\times [0;1])/(X\times \{1\}):=(X\times [0;1])/\sim$

als den Faktorraum und betrachte die kanonische Projektion

$p\colon X\times [0;1]\to CX;x\mapsto [x]_{\sim }$ .

Eine Teilmenge $U\subseteq CX$ soll nun genau dann offen heißen, wenn ihr Urbild $p^{{-1}}(U)$ offen in $X\times [0;1]$ ist. Das System dieser offenen Mengen bildet tatsächlich eine Topologie auf , der so entstehende Raum ist der Kegel über .

Anschaulich gesprochen wird die Deckfläche des Zylinders $X\times [0;1]$ zu einem einzigen Punkt zusammengeschlagen.

Eigenschaften

Jeder topologische Raum lässt sich als Teilraum seines Kegels auffassen, indem man mit $X\times \{1\}$ identifiziert.

Der Kegel eines nicht-leeren Raumes ist stets zusammenziehbar, vermöge der Homotopie .
- Zusammen mit der ersten Eigenschaft ergibt sich eine kanonische Einbettung eines beliebigen (nicht-leeren) in einen zusammenziehbaren Raum, was die Bedeutung des Kegels in der algebraischen Topologie begründet.

Der Kegel über einem topologischen Raum ist zu dem Abbildungskegel der Identität dieses Raumes homöomorph.

Jeder Kegel ist wegzusammenhängend, also insbesondere auch zusammenhängend.

Lässt sich in einen Euklidischen Raum einbetten, so ist zu einem geometrischen Kegel homöomorph.
- Besondere Bedeutung hat hier der Fall, dass eine zusammenhängende, kompakte Teilmenge des $\mathbb {R} ^{2}$ ist. (siehe Beispiele)

Ist allgemeiner kompakt und Hausdorffsch, so entspricht sein Kegel der Vereinigung aller Strecken von Punkten $x\in X$ zu einer gemeinsamen Spitze.

Ist ein CW-Komplex, so auch .

Beispiele

Der Kegel über einem -Simplex ist ein -Simplex.
- Für einen Punkt $x\in \mathbb {R} ^{n}$ ist insbesondere $C\{x\}$ eine Strecke, $C(C\{x\})$ ein Dreieck und $C(C(C\{x\}))$ ein Tetraeder.
Der Kegel über einem Polygon entspricht der Pyramide mit Grundfläche
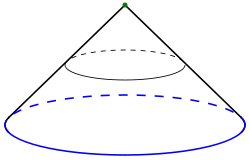
Der topologische Kegel über einem ausgefüllten Kreis ist der klassische Kreiskegel. (siehe Abbildung)
Der topologische Kegel über einer Kreislinie ist die Mantelfläche eines Kreiskegels; diese wiederum ist topologisch äquivalent zum Vollkreis, indem man anschaulich gesprochen die Spitze eindrückt.
- Allgemein gilt die Homöomorphie $CS^{{n-1}}\cong D^{n}$ .

Reduzierter Kegel

Sei nun $(X;x_{0})$ ein punktierter Raum, so ist der reduzierte Kegel über definiert als

$C_{*}X=X\times [0,1]/(X\times \left\{0\right\})\cup (\left\{x_{0}\right\}\times [0,1])$

mit der Quotiententopologie.

Mit $[(x_{0};0)]_{\sim }$ als Basispunkt wird $C_{*}X$ selbst wieder zu einem punktierten Raum und die oben erwähnte Inklusion $x\mapsto [(x;1)]_{\sim }$ zu einer basispunkterhaltenden Einbettung.

Der reduzierte Kegel ist gleich dem reduzierten Abbildungskegel der Identität.

Kegelfunktor

In der Kategorientheorie induziert die Zuordnung $X\mapsto CX$ einen Endofunktor $C:\mathbf {Top} \to \mathbf {Top}$ auf der Kategorie $\mathbf{Top}$ der topologischen Räume.

Dieser ordnet außerdem jeder stetigen Abbildung $f\in \operatorname {Mor}(X;Y)$ diejenige Abbildung $C(f)\in \operatorname {Mor}(CX;CY)$ zu, die durch $[(x;t)]_{{\sim _{{CX}}}}\mapsto [(f(x);t)]_{{\sim _{{CY}}}}$ erklärt wird.

Das Gleiche gilt für $X\mapsto C_{*}X$ in der Kategorie $\mathbf {Top*}$ der punktierten topologischen Räume.

Hinweis: Die hier verwendete Notation sollte nicht mit dem Abbildungskegel für stetiges oder dem Funktionenraum ${\mathcal C}(X)$ aller stetigen Abbildungen auf einem topologischen Raum verwechselt werden.

Siehe auch

Einhängung

Basierend auf einem Artikel in:

Wikipedia.de