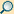Schiefer Ellipsenkegel

schiefer elliptischer Kegel

Der schiefe Ellipsenkegel (englisch: oblique cone) ist eine Verallgemeinerung des schiefen Kreiskegels; seine Grundfläche ist eine Ellipse mit entsprechenden Halbachsen und . Die Spitze des Schiefkegels braucht nicht über dem Ellipsenzentrum zu liegen, sondern kann sich über $S_{0}=(u,v)$ befinden.

Grundfläche

Die Grundfläche wird von einer Ellipse gebildet:

$A=\pi ab=\pi a^{2}{\sqrt {1-\varepsilon ^{2}}}$

Mit als Länge der großen und der kleinen Halbachsen und

$\varepsilon ={\frac {\sqrt {a^{2}-b^{2}}}{a}}\in [0,1)$

Volumen

Für das Volumen gilt die verallgemeinerte Formel des schiefen Kreiskegels:

$V={\frac {1}{3}}hA={\frac {1}{3}}h\pi ab={\frac {\pi }{3}}hab$

mit als Höhe des schiefen Kegels,

$a={\frac {d_{\mathrm {max} }}{2}}$

als Länge der großen (halber maximaler Durchmesser) und

$b={\frac {d_{\mathrm {min} }}{2}}$

der kleinen Halbachsen (halber minimaler Durchmesser).

Faustformel

$1{,}0498\cdot hab\geq V={\frac {\pi }{3}}hab\geq 1{,}0497\cdot hab\geq hab$

Der Fehler bei Verwendung von $hab$ zur Berechnung des Volumens ist somit kleiner als 5 % (Faktor 1,05) und kann bei einer Abschätzung vernachlässigt werden.

Generell: Mantel des schiefen Ellipsenkegels

schiefer Ellipsenkegel

Die Berechnung der Mantelfläche ist anspruchsvoll.

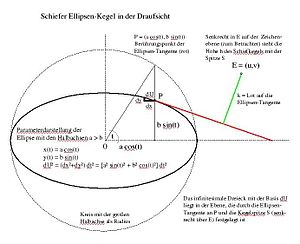
Die Ellipse wird durch

$x(t)=a\cdot \cos(t)$

$y(t)=b\cdot \sin(t)$

beschrieben ( aus $[0,2\pi]$ , Parameterdarstellung, siehe Zeichnung).

Es sei

$N(t):={\sqrt {a^{2}\cdot \sin(t)^{2}+b^{2}\cdot \cos(t)^{2}}}$

Die Basis des infinitesimalen Dreiecks (die zur Berechnung des Kegelmantels verwendet wird) ist

$dU=N(t)\cdot \mathrm {d} t$

das folgt durch Differentiation aus der obigen Parameterdarstellung. In der Literatur wird N(t) häufig als

$N(t)=a\cdot {\sqrt {1-n^{2}\cdot \cos(t)^{2}}}$

geschrieben. mit $n^{2}=(a^{2}-b^{2})/a^{2}$ heißt „numerische Exzentrizität“. Die Integration von t=0 bis $2\pi$ ergibt ein „elliptisches Integral zweiter Gattung“ (das ist die bekannte Formel für den Umfang einer Ellipse). Das infinitesimale Dreieck liegt in der Ebene, die durch die Ellipsen-Tangente an

$P=(a\cdot \cos(t),b\cdot \sin(t))$

und durch die Kegelspitze im Abstand senkrecht über $E=(u,v)$ festgelegt ist. Die Höhe des infinitesimalen Dreiecks lautet

$f(t)={\sqrt {k(t)^{2}+h^{2}}}$

(nicht zu verwechseln mit der Höhe des Kegels). Hier bedeutet $k(t)$ das Lot von auf die Ellipsen-Tangente an den Punkt . Es sei

$Z(t):=ab-va\cdot \sin(t)-ub\cdot \cos(t)$

Dann gilt

$k(t)={\frac {Z(t)}{N(t)}}$

Die Fläche des infinitesimalen Dreiecks beträgt also

${\frac {1}{2}}\cdot f(t)\cdot N(t)\cdot dt={\frac {1}{2}}{\sqrt {Z(t)^{2}+h^{2}\cdot N(t)^{2}}}\mathrm {d} t$

Die Formel für die Mantelfläche M des schiefen Ellipsenkegels lautet demnach:

$M={\frac {1}{2}}\int \limits _{0}^{2\pi }{\sqrt {Z(t)^{2}+h^{2}\cdot N(t)^{2}}}\mathrm {d} t$

Da der Integrand nicht symmetrisch um $\pi$ verläuft, muss man hier über den Vollkreis integrieren. Unter dem Integral von 0 bis $2\pi$ darf man die Minuszeichen in $Z(t)$ gemeinsam durch Pluszeichen ersetzen. Dann lautet die Formel ausgeschrieben

$M={\frac {1}{2}}\int \limits _{0}^{2\pi }{\sqrt {(ab+va\cdot \sin(t)+ub\cdot \cos(t))^{2}+h^{2}\cdot (a^{2}\cdot \sin(t)^{2}+b^{2}\cdot \cos(t)^{2})}}\mathrm {d} t$

Statt $0$ und $2\pi$ kann man auch $-\pi$ und $\pi$ als Integrationsgrenzen wählen, ohne den Wert zu ändern. Wenn man als Funktion von $a,b,u,v$ und auffasst, dann dient sie als Erzeugende der bekannten Formeln für Kreis, Ellipse und Kegel.

$M(r,r,0,0,0)$ = Kreisfläche

$M(a,b,0,0,0)$ = Ellipsenfläche

$M(r,r,0,0,h)$ = Mantelfläche des geraden Kreiskegels

$M(r,r,e,0,h)=M(r,r,0,e,h)$ = Mantelfläche des schiefen Kreiskegels

$M(a,b,0,0,h)$ = Mantelfläche des geraden Ellipsenkegels

$M(a,b,u,v,h)$ = Mantelfläche des schiefen Ellipsenkegels.

Ein Extremalwertsatz

Bewegt man die Spitze des schiefen Ellipsenkegels auf gleichbleibender Höhe (bzw. mit konstanter Achse) über den Strahl $v(u)=cu$ (c beliebige Steigung), dann ist der Mantel eine differenzierbare Funktion von (bei u = 0 eine Funktion von v). Es gilt $M'(0)=0$ und $M''(0)>0$ (bzw. $M''(0)<0$ ) und damit der Satz (analog zum Kreiskegel)

Unter allen Ellipsenkegeln derselben Höhe (derselben Achse) über derselben Grundellipse besitzt der gerade den kleinsten (bzw. größten) Mantel.

Beim Beweis verwendet man die Tatsache, dass sich die Differentiation nach unter das Integral ziehen lässt und dass folgende Integranden, über den Vollkreis integriert, verschwinden: $G(t)\sin(t)$ , $G(t)\sin(2t)$ und $G(t)\cos(t)$ , wobei G(t) eine Funktion bezeichnet, die um ${\frac {i}{2}}\pi \ (i=1,2,3)$ symmetrisch verläuft, z.B. $G(t)=\cos(2t)$ oder $G(t)=a^{2}\sin(t)^{2}+b^{2}\cos(t)^{2}$ .

Speziell: Mantel des geraden Ellipsenkegels

Für $u=v=0$ (also für den geraden Ellipsenkegel) lautet die Mantel-Formel

$M={\frac {1}{2}}\int \limits _{0}^{2\pi }{\sqrt {a^{2}b^{2}+h^{2}\cdot (a^{2}\cdot \sin(t)^{2}+b^{2}\cdot \cos(t)^{2})}}\mathrm {d} t$

Durch den erlaubten Kniff

$a^{2}b^{2}=a^{2}b^{2}\cdot (\sin(t)^{2}+\cos(t)^{2})$

lässt sich der Integrand nach $\sin(t)^{2}$ und $\cos(t)^{2}$ ordnen, und man erhält den Ausdruck

$M={\frac {1}{2}}\int \limits _{0}^{2\pi }{\sqrt {A^{2}\cdot \sin(t)^{2}+B^{2}\cdot \cos(t)^{2}}}\mathrm {d} t$

wobei $A^{2}:=a^{2}(b^{2}+h^{2})$ und $B^{2}:=b^{2}(a^{2}+h^{2})$ . Das Integral (ohne den Faktor ½) bedeutet den Umfang der Ellipse mit den Halbachsen und . Daher gilt der Satz:

Die Mantelfläche des geraden Ellipsenkegels mit den Halbachsen und und der Höhe ist zahlenmäßig gleich dem halben Umfang der Ellipse mit den Halbachsen und

Der Nutzen dieses Satzes besteht darin, dass man nun die bekannten Abschätzungen für den Ellipsenumfang auf die Mantel-Berechnung anwenden darf. Für den Umfang der Ellipse mit den Halbachsen und gilt in erster Näherung ( $a\neq b$ und h>0 , also auch $A\neq B$ )

$U>\pi \cdot (A+B)$

Für den Mantel des geraden Ellipsenkegels gewinnt man daraus die Abschätzung

$M>{\frac {1}{2}}\cdot \pi \cdot \left(a\cdot {\sqrt {b^{2}+h^{2}}}+b\cdot {\sqrt {a^{2}+h^{2}}}\right)$

Das Gleichheitszeichen gilt für a=b (Mantel des geraden Kreiskegels) oder h=0 (Ellipsen- bzw. Kreisfläche). Beispiel: a = 3 , b = 2 und h = 4 . Die Abschätzung liefert den Wert 36,7… Der genaue Wert beträgt 36,9…

Schlussbemerkung: Durch Abschätzung des Integranden nach unten und oben erhält man die grobe Ungleichung $\pi B<M<\pi A$ für b<a (das Gleichheitszeichen gilt für a=b oder h=0 ). Die Mantelfläche ist also ungefähr gleich dem arithmetischen Mittel aus der unteren und oberen Schranke.

Siehe auch

Schiefer Kreiskegel
Schiefer Kegel (allgemein)

Basierend auf einem Artikel in:

Wikipedia.de