Cassinische Kurve

Cassinische Kurven mit
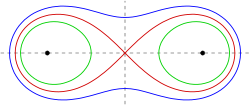
a<c a=c a>c

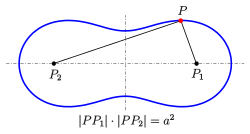
Die Cassinische Kurve (benannt nach Giovanni Domenico Cassini) ist der Ort aller Punkte in der Ebene, für die das Produkt ihrer Abstände von zwei gegebenen Punkten $P_{1}$ und $P_{2}$ gleich $a^{2},a\in \mathbb {R} _{0}^{+}$ ist. Von Giovanni Domenico Cassini wurden diese Kurven auch nach Entdeckung der keplerschen Gesetze als Planetenbahnen vorgeschlagen. Ein Spezialfall der Cassinischen Kurve ist die Lemniskate von Bernoulli.

Man sollte die Definition einer Cassinischen Kurve nicht mit der Definition einer Ellipse verwechseln: Bei einer Ellipse ist die Summe der Abstände konstant.

Gleichungen

Cassinische Kurve: Definition

Die Kurve lässt sich in kartesischen Koordinaten durch die Gleichung

$(x^{2}+y^{2})^{2}-2c^{2}(x^{2}-y^{2})=a^{4}-c^{4}\qquad a,c\in \mathbb {R} _{0}^{+}$

beschreiben, wobei $P_{1}=(c,0)$ und $P_{2}=(-c,0)$ gesetzt wurde. In Polarkoordinaten lautet die Gleichung

$r^{2}=c^{2}\cos(2\varphi )\pm {\sqrt {c^{4}\cos ^{2}(2\varphi )+(a^{4}-c^{4})}}\qquad a,c\in \mathbb {R} _{0}^{+}.$

Herleitung aus der Definition

Das Problem werde in einem rechtwinkligen kartesischen Koordinatensystem der Ebene behandelt, sodass $P_{1}=P(c,0)$ und $P_{2}=(-c,0)$ , mit $c\in \mathbb {R} _{0}^{+}$ gilt. Dann gilt für einen Punkt $P=(x,y)$ auf der Kurve laut Definition:

${\begin{array}{rcl}a^{2}&=&|PP_{1}|\cdot |PP_{2}|={\sqrt {(x+c)^{2}+y^{2}}}{\sqrt {(x-c)^{2}+y^{2}}}\\a^{4}&=&[(x+c)^{2}+y^{2}][(x-c)^{2}+y^{2}]=(x^{2}-c^{2})^{2}+y^{2}[(x+c)^{2}+(x-c)^{2}]+y^{4}\\&=&(x^{4}-2x^{2}c^{2}+c^{4})+y^{2}[2x^{2}+2c^{2}]+y^{4}=x^{4}+2x^{2}y^{2}+y^{4}+c^{4}-2c^{2}x^{2}+2c^{2}y^{2}\\a^{4}-c^{4}&=&(x^{2}+y^{2})^{2}-2c^{2}(x^{2}-y^{2}).\end{array}}$

Für den Übergang in Polarkoordinaten ist die Transformation $x=r\cos(\varphi ),y=r\sin(\varphi )$ nötig. Es ergibt sich mit dem „trigonometrischen Pythagoras“:

$a^{4}-c^{4}=r^{4}-2c^{2}r^{2}(\cos ^{2}(\varphi )-\sin ^{2}(\varphi ))=r^{4}-2c^{2}r^{2}\cos(2\varphi ).$

Dies ist eine Quartische Gleichung, insbesondere handelt es sich hier um den biquadratischen Spezialfall, der als Quadratische Gleichung in $r^{2}$ zu lösen ist:

$(r^{2})^{2}-2c^{2}\cos(2\varphi )\cdot r^{2}-(a^{4}-c^{4})=0$

$\Rightarrow r^{2}(\varphi )=c^{2}\cos(2\varphi )\pm {\sqrt {c^{4}\cos ^{2}(2\varphi )+(a^{4}-c^{4})}}.$

Form der Kurve

Die Cassinischen Kurven für verschiedene b=a/c:

b = 0,6	b = 0,8	b = 1
b = 1,2	b = 1,4	b = 1,6

Die Form der Cassinischen Kurve lässt sich in fünf Fälle unterscheiden:

1. Fall: Für $a>c{\sqrt {2}}$ ist die Kurve ein ungefähr ellipsenförmiges Oval. Ihre Schnittpunkte mit der x-Achse liegen in diesem Fall bei $(\pm {\sqrt {a^{2}+c^{2}}},\,0)$ , die Schnittpunkte mit der y-Achse bei $(0,\pm {\sqrt {a^{2}-c^{2}}})$ .

2. Fall: Für $a=c{\sqrt {2}}$ ergibt sie wieder ein ungefähr ellipsenförmiges Oval. Die Schnittpunkte mit der x-Achse liegen nun bei $(\pm c{\sqrt {3}},\,0)$ . An den Schnittpunkten mit der y-Achse bei $(0,\,\pm c)$ ist die Krümmung der Kurve gleich 0.

3. Fall: Für $c<a<c{\sqrt {2}}$ ergibt sich ein eingedrücktes Oval mit den gleichen Achsenabschnitten wie im 1. Fall $a>c{\sqrt {2}}$ . Neben den beiden y-Achsenabschnitten sind die weiteren Extrema der Kurve an den Punkten

${\frac {1}{2c}}\left(\pm {\sqrt {4c^{4}-a^{4}}},\ \pm a^{2}\right)$

Die vier Wendepunkte liegen bei

$\left(\pm {\sqrt {{\tfrac {1}{2}}(m-n)}},\,\pm {\sqrt {{\tfrac {1}{2}}(m+n)}}\right)\quad {\text{mit}}\quad m={\sqrt {\tfrac {a^{4}-c^{4}}{3}}}\quad {\text{und}}\quad n={\tfrac {a^{4}-c^{4}}{3c^{2}}}$

4. Fall: Für ergibt sich die Lemniskate.

5. Fall

Für

ergeben sich zwei Ovale um die Punkte $(c,0)$ und $(-c,0)$ . Die Schnittpunkte mit der x-Achse haben die x-Koordinaten

$\pm {\sqrt {c^{2}\pm a^{2}}}$

Die Extrema sind an den Punkten

${\frac {1}{2c}}\left(\pm {\sqrt {4c^{4}-a^{4}}},\ \pm a^{2}\right)$

Cassinische Kurven und Orthogonaltrajektorien

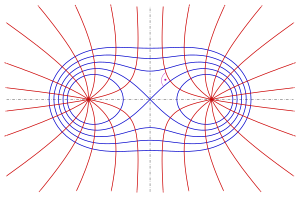
Cassinische Kurven und dazu orthogonale Hyperbeln

Orthogonaltrajektorien einer gegebenen Kurvenschar sind Kurven, die alle gegebenen Kurven orthogonal schneiden. So sind z.B. zu einer Schar konfokaler Ellipsen die zugehörigen konfokalen Hyperbeln Orthogonaltrajektorien. Für Cassinische Kurven gilt:

Die Orthogonaltrajektorien der Cassinischen Kurven zu zwei Punkten sind die gleichseitigen Hyperbeln durch $P_{1},P_{2}$ mit dem Mittelpunkt von $P_{1},P_{2}$ als Mittelpunkt (s. Bild).

Beweis:
Um die Rechnung einfach zu gestalten, seien $P_{1}=(1,0),\;P_{2}=(-1,0)$ .

Die cassinischen Kurven genügen der Gleichung

$f(x,y)\;=\;(x^{2}+y^{2})^{2}-2(x^{2}-y^{2})+1-a^{4}=0$ .

Die gleichseitigen Hyperbeln (d.h. ihre Asymptoten stehen senkrecht aufeinander) durch $(1,0),(-1,0)$ und Mittelpunkt (0,0)

genügen der Gleichung

$y^{2}-x^{2}+\lambda xy+1=0,\quad \lambda \in \mathbb {R} .$

Die Hyperbeln schneiden die y-Achse nicht und die x-Achse nur in $(\pm 1,0)$ . Eine Hauptachsentransformation zeigt, dass es sich tatsächlich um gleichseitige Hyperbeln mit dem Ursprung als Mittelpunkt handelt. Mit Punktproben erkennt man: $(1,0),(-1,0)$ liegen auf den Hyperbeln. Um eine vom Parameter unabhängige Normale der Hyperbeln zu erhalten, benutzt man besser die folgende implizite Darstellung:

$g(x,y)\;=\;{\frac {x^{2}-y^{2}-1}{xy}}-\lambda ={\frac {x}{y}}-{\frac {y}{x}}-{\frac {1}{xy}}-\lambda =0\;.$

Für den Nachweis, dass sich die Hyperbeln und die cassinischen Kurven senkrecht schneiden, zeigt man, dass $\operatorname {grad} f(x,y)\cdot \operatorname {grad} g(x,y)=0$ ist für alle Punkte $(x,y),\;x\neq 0\neq y$ . Dies ist rechnerisch leicht nachvollziehbar, da die beiden Scharparameter beim Differenzieren herausfallen.

Bemerkung:
Das Bild der cassinischen Kurven und den dazu orthogonalen Hyperbeln ist den Feld- und Potentiallinien zweier gleicher Punktladungen ähnlich aber nicht gleich. Bei einer Äquipotentiallinie zweier Punktladungen ist die Summe der Kehrwerte der Abstände zu zwei festen Punkten konstant: ${\frac {1}{|PP_{1}|}}+{\frac {1}{|PP_{2}|}}={\text{konstant}}$ . (Siehe >implizite Kurven)

Cassinische Kurven auf Tori

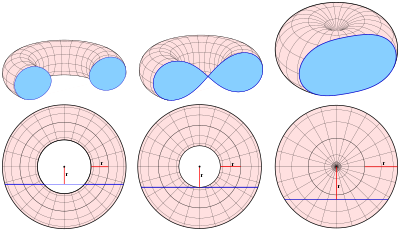
Cassinische Kurven als ebene Schnitte eines Torus
(der rechte Torus ist ein Spindeltorus)

Cassinische Kurven treten auch als ebene Schnitte von Tori auf. Allerdings nur dann, wenn die

schneidende Ebene parallel zur Torusachse und der Abstand von der Torusachse gleich dem Radius des erzeugenden Kreises ist (s. Bild).

Schneidet man den Torus mit der Gleichung

$\left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\left(x^{2}+y^{2}\right).$

mit der Ebene $y=r$ so erhält man zunächst:

$\left(x^{2}+z^{2}+R^{2}\right)^{2}=4R^{2}\left(x^{2}+r^{2}\right).$

Nach dem teilweisen Auflösen der ersten Klammer ergibt sich

$\left(x^{2}+z^{2}\right)^{2}-2R^{2}(x^{2}-z^{2})=4R^{2}r^{2}-R^{4}.$

Die - und -Koordinaten der Schnittkurve erfüllen die Gleichung einer Cassinischen Kurve mit den Parametern $a^{2}=2Rr,\;c=R$ .

Flächeninhalt und Umfang

Flächeninhalt:

Die Cassinischen Kurven können folgendermaßen parametrisiert werden:

$x={\frac {a^{2}{\sqrt {a^{2}+c^{2}}}\cos(\vartheta )}{a^{2}+c^{2}\sin(\vartheta )^{2}}}$ und $y={\frac {{\sqrt {a^{2}+c^{2}}}\sin(\vartheta ){\sqrt {a^{4}-c^{4}\sin(\vartheta )^{2}}}}{a^{2}+c^{2}\sin(\vartheta )^{2}}}$

Diese Parametrisierung erfüllt die Gleichung für kartesische Koordinaten:

$(x^{2}+y^{2})^{2}-2c^{2}(x^{2}-y^{2})=a^{4}-c^{4}$

Der Flächeninhalt der Cassinischen Kurven für den Fall a > c kann auf folgende Weise ermittelt werden:

$A=4\int _{0}^{\sqrt {a^{2}+c^{2}}}|y(x)|dx=4\int _{0}^{\pi /2}\left[-{\frac {\mathrm {d} }{\mathrm {d} \vartheta }}x(\vartheta )\right]y(\vartheta )\mathrm {d} \vartheta =$

$=4\int _{0}^{\pi /2}\left[-{\frac {\mathrm {d} }{\mathrm {d} \vartheta }}{\frac {a^{2}{\sqrt {a^{2}+c^{2}}}\cos(\vartheta )}{a^{2}+c^{2}\sin(\vartheta )^{2}}}\right]{\frac {{\sqrt {a^{2}+c^{2}}}\sin(\vartheta ){\sqrt {a^{4}-c^{4}\sin(\vartheta )^{2}}}}{a^{2}+c^{2}\sin(\vartheta )^{2}}}\mathrm {d} \vartheta =$

$=4\int _{0}^{\pi /2}{\frac {a^{2}{\sqrt {a^{2}+c^{2}}}\sin(\vartheta )^{2}[a^{2}+2c^{2}-c^{2}\sin(\vartheta )^{2}]{\sqrt {a^{4}-c^{4}\sin(\vartheta )^{2}}}}{[a^{2}+c^{2}\sin(\vartheta )^{2}]^{3}}}d\vartheta =$

$=4\int _{0}^{\pi /2}{\frac {\mathrm {d} }{\mathrm {d} \vartheta }}\left[{\frac {a^{2}}{2}}E(\vartheta ;c^{2}/a^{2})-{\frac {\sin(\vartheta )\cos(\vartheta )[a^{4}-c^{4}\sin(\vartheta )^{2}]^{3/2}}{2[a^{2}+c^{2}\sin(\vartheta )^{2}]^{2}}}\right]d\vartheta =2a^{2}E(c^{2}/a^{2})$

Endresultat:

$A=2a^{2}E(c^{2}/a^{2})$

Bei dieser Formel ist E das vollständige elliptische Integral zweiter Art.

Bei der Lemniskate von Bernoulli ist c = a und somit gilt: A = 2*a^2*E(1) = 2*a^2

Umfang:

Der Umfang der Cassinischen Kurven für den Fall a > c kann auf folgende Weise ermittelt werden:

$U=4\int _{0}^{\pi /2}{\sqrt {\left[{\frac {\mathrm {d} }{\mathrm {d} \vartheta }}x(\vartheta )\right]^{2}+\left[{\frac {\mathrm {d} }{\mathrm {d} \vartheta }}y(\vartheta )\right]^{2}}}\mathrm {d} \vartheta =$

$=4\int _{0}^{\pi /2}{\sqrt {\left[{\frac {\mathrm {d} }{\mathrm {d} \vartheta }}{\frac {a^{2}{\sqrt {a^{2}+c^{2}}}\cos(\vartheta )}{a^{2}+c^{2}\sin(\vartheta )^{2}}}\right]^{2}+\left[{\frac {\mathrm {d} }{\mathrm {d} \vartheta }}{\frac {{\sqrt {a^{2}+c^{2}}}\sin(\vartheta ){\sqrt {a^{4}-c^{4}\sin(\vartheta )^{2}}}}{a^{2}+c^{2}\sin(\vartheta )^{2}}}\right]^{2}}}\mathrm {d} \vartheta =$

$=4\int _{0}^{\pi /2}{\frac {a^{2}{\sqrt {a^{2}+c^{2}}}{\sqrt {a^{2}-c^{2}\sin(\vartheta )^{2}}}}{{\sqrt {a^{2}+c^{2}\sin(\vartheta )^{2}}}{\sqrt {a^{4}-c^{4}\sin(\vartheta )^{2}}}}}\mathrm {d} \vartheta =4{\sqrt {a^{2}+c^{2}}}\int _{0}^{1}{\frac {\sqrt {1-(c/a)^{2}w^{2}}}{\sqrt {[1+(c/a)^{2}w^{2}][1-(c/a)^{4}w^{2}](1-w^{2})}}}dw$

Endresultat:

$U=4{\sqrt {a^{2}+c^{2}}}\int _{0}^{1}{\frac {\sqrt {1-(c/a)^{2}w^{2}}}{\sqrt {[1+(c/a)^{2}w^{2}][1-(c/a)^{4}w^{2}](1-w^{2})}}}dw$

Für die Theta-Werte von 0 bis pi/2 wird ein Viertel der gesamten Kurve parametrisiert.

Verallgemeinerungen

Die Konstruktion einer Cassinischen Kurve lässt sich leicht auf ebene Kurven und Flächen mit beliebig vielen Grundpunkten verallgemeinern:

$|PP_{1}|\cdot |PP_{2}|\cdots |PP_{n}|=a^{n}$

beschreibt im ebenen Fall eine implizite Kurve und im 3-dimensionalen Raum eine implizite Fläche.

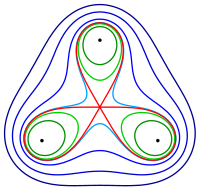verallgem. Kurven zu 3 Punkten
verallgem. Fläche zu 6 Punkten

Literatur

Bronstein u. a.: Taschenbuch der Mathematik. Verlag Harri Deutsch, Frankfurt am Main 2005, ISBN 3-8171-2006-0.
I. Agricola,T. Friedrich: Elementargeometrie: Fachwissen für Studium und Mathematikunterricht, Springer-Spektrum, 2015, ISBN 978-3-658-06730-4, S. 60.

Basierend auf einem Artikel in:

Wikipedia.de