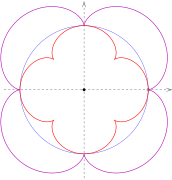
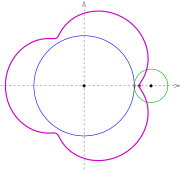
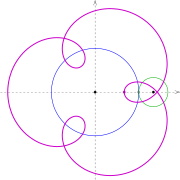
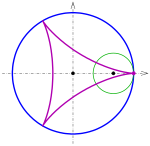
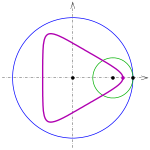
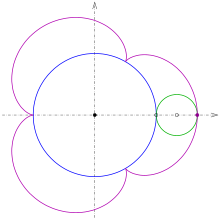
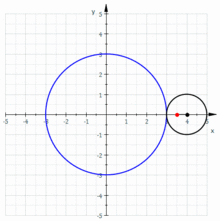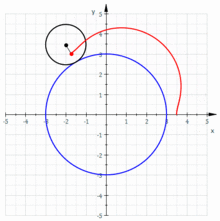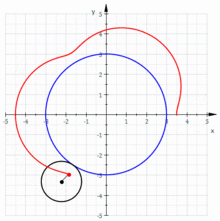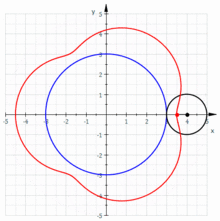
Epizykloide
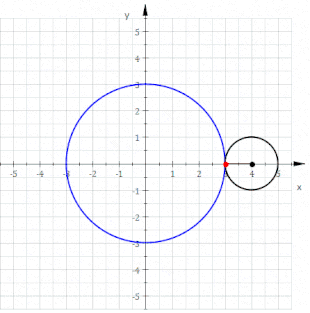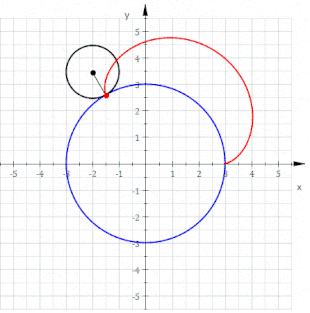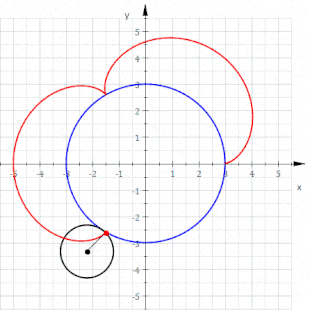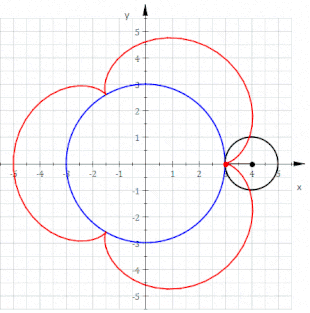
Wenn ein Kreis vom Radius
außen auf einem Kreis vom Radius
abrollt,
beschreibt ein Punkt auf dem Kreisumfang eine Epizykloide. Bei einer Zykloide
rollt ein Kreis auf einer Geraden.
Auf diese Weise lassen sich mandalaähnliche Figuren zeichnen, die auch Blumen ähneln.
Eine Epizykloide ist ein Sonderfall einer Epitrochoide.
Rollt der kleine Kreis in dem großen Kreis, entsteht eine Hypozykloide bzw. Hypotrochoide. Siehe auch den Artikel über Zykloide.
Parameterdarstellung
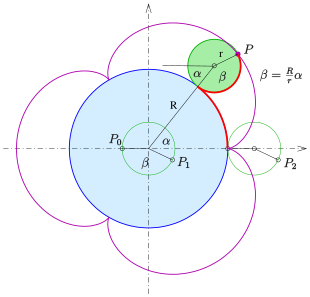
Beim Abrollen des kleinen Kreises dreht sich der kleine Kreis um einen Winkel
.
Dabei wird auf dem großen Kreis der Winkel
(siehe Bild) überstrichen. Da beide Kreisbögen gleich lang sind, muss
und damit
sein.
Ein Kurvenpunkt
kann man sich durch folgende Operationen entstanden denken:
- Drehung des Punktes
um den Nullpunkt mit Winkel
ergibt
,
- Verschiebung von
um
nach rechts ergibt
,
- Drehung von
um den Nullpunkt mit Winkel
ergibt den Kurvenpunkt
.
Diese Operationen kann man in x-y-Koordinaten mit Hilfe von Drehmatrizen
ausführen. Betrachtet man die Ebene als Darstellung der komplexen Zahlen, wird
die Rechnung leicht und übersichtlich. Denn die Drehung eines Punktes (einer
komplexen Zahl)
um den Winkel
ergibt
:
- Für
ergibt sich
,
,
In x-y-Koordinaten bedeutet dies:
Und mit
schließlich
Für Untersuchungen ist die folgende Form von Vorteil. Mit
ist:
Wenn das Verhältnis
eine rationale Zahl ist, schließt sich die Kurve nach mehreren Umdrehungen. Ist
es irrational, schließt sie sich nie.
Weitere Beispiele
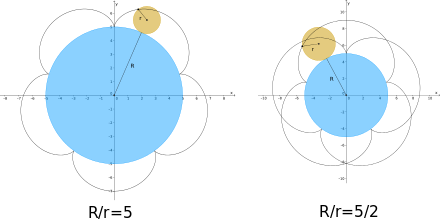
In dem folgenden Schaubild ist links
eine ganze Zahl, deswegen überlappen sich die „Blütenblätter“ links nicht und
die Kurve ist geschlossen. Rechts überlappen sich aber die „Blütenblätter“,
d.h., die Kurve ist nicht geschlossen, da
.
wird auch Ordnung der Epizykloide genannt.
Länge, Fläche, Evolute
Die ersten Ableitungen der letzten Parameterdarstellung sind
und
(Es wurden die Formeln
verwendet.)
- Länge
Eine sich schließende Epizykloide besitzt
Bögen. Die Länge eines Bogens der Zykloide ist
und die Gesamtlänge ist

- Flächeninhalt
Mit der Sektorformel von Leibniz
und
ergibt sich für den Sektor-Flächeninhalt zu einem Bogen
und für die ganze Kurve (
Bögen)
- Evolute
Wegen
ist
(siehe oben)
und die Parameterdarstellung der Evolute ist
Das ist die Gleichung einer Epizykloide, die aus der gegebenen Epizykloide
durch Skalierung mit dem Faktor
verkleinert und um
(im Bild
)
gedreht ist (siehe nächsten Abschnitt).
Das nächste Bild zeigt ein weiteres Beispiel einer Zykloide mit
und ihre Evolute. Im zweiten Beispiel ist
.
In diesem Fall schließt sich die Epizykloide erst nach zwei Durchgängen, da
keine ganze Zahl ist.
Alternative Definition und Parameterdarstellung
Verwendet man zur Definition einer Epizykloide die Bahn des Punktes ,
so entsteht eine zur obigen Definition um den Winkel
gedrehte Kurve. Ihre Parameterdarstellung ist:
Spezielle Epizykloiden
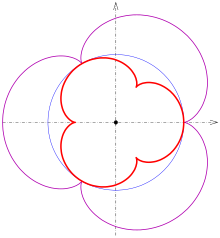
Kardioide
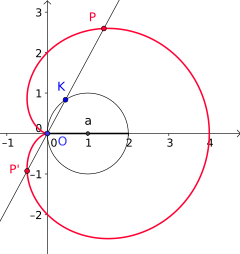
Für
ergibt sich eine Kardioide
(Herzkurve). Für Umfang und Fläche erhält man:
Wenn die Spitze der Kardioide im Koordinatenursprung liegt, lautet die Gleichung in Polar- bzw. kartesischen Koordinaten:
Es sei ein innerer Kreis mit Radius ,
dessen Mittelpunkt der Koordinatenursprung eines kartesischen
Koordinatensystems und der darauf abrollende Kreis mit Radius
Um den Punkt
auf dem Radius
innerhalb eines Quadranten – vorteilhaft zwischen den Koordinatenachsen – zu
bestimmen, bedarf es nur einer Verbindung der Kreismittelpunkte und der
Übertragung des Mittelpunktswinkels
(siehe Bild) vom inneren Kreis (blau) auf das Zentrum des abrollenden Kreises
(grün). Der Winkelschenkel des Winkels
erzeugt mit
(rot) den Punkt, der die Kardioide als Ortskurve
liefert.
Diese Kurve kann man auch anders erhalten, und zwar als Kreiskonchoide (Pascalsche Schnecke): Man zeichnet von einem Punkt auf dem Kreisumfang eine Sehne und verlängert sie um den Kreisdurchmesser. Wenn die Sehne sich dreht, beschreibt der Endpunkt der Verlängerung eine Kardioide.
Nephroide
Ist
sprich
so erhält man, wie im Folgenden beschrieben, eine Nephroide. Sie hat die
Maße
Es sei ein innerer Kreis mit Radius ,
dessen Mittelpunkt der Koordinatenursprung eines kartesischen Koordinatensystems
und der darauf abrollende Kreis mit Radius
Um den Punkt
auf dem Radius
innerhalb eines Quadranten – vorteilhaft zwischen den Koordinatenachsen – zu
bestimmen, verbindet man zuerst die Mittelpunkte der beiden Kreise. Der dabei im
Winkelscheitel
des inneren Kreises entstandene Mittelpunktswinkel
(siehe Bild) wird nun mit der Winkelweite
in das Zentrum des abrollenden Kreises (grün) mit positivem Drehsinn
eingearbeitet. Der Winkelschenkel des Winkels
erzeugt mit
(rot) den Punkt, der die Nephroide als Ortskurve liefert.
Für die dargestellte Nephroide gilt die Gleichung
mit dem eingesetzten Wert
ergibt sich schließlich
Epitrochoide
Geht man bei der Herleitung der Parameterdarstellung (s.o.) einer
Epizykloide von einem Punkt
aus, erhält man die Parameterdarstellung einer Epitrochoide:
Mit
ist:
ist der Abstand des Startpunktes (
)
zum Mittelpunkt des kleinen Startkreises.
Eine Epizykloide ist mit
ein Sonderfall einer Epitrochoide.
Hypozykloide, Hypotrochoide
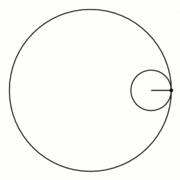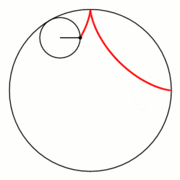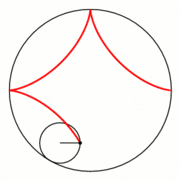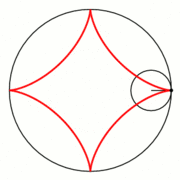
In diesem Fall rollt der kleine Kreis mit Radius
in dem großen Kreis mit Radius
.
Die Beziehung zwischen den Winkeln
und
bleibt erhalten. Allerdings dreht sich der kleine Kreis hier im
Uhrzeigersinn. Geht man bei der Herleitung der Parameterdarstellung einer
Epizykloide (siehe oben) von dem Punkt
aus, dreht den kleinen Kreis im Uhrzeigersinn und verschiebt nur um
,
so erhält man die Parameterdarstellung einer Hypotrochoide:
Mit
ist:
Für
erhält man eine Hypozykloide.
Für
ist
und die
- Hypozykloide (
) der Durchmesser des großen Kreises mit
- Hypotrochoide (
) die Ellipse
Für
liegt die große Achse der Ellipsen auf der x-Achse, für
auf der y-Achse. Für
ergibt sich ein Kreis.
Eine Ellipse
lässt sich also auch immer durch eine Hypotrochoide mit den Parametern
erzeugen.
Ein Kreispaar, bei dem der kleine Kreis den halben Radius des großen Kreises hat, und der kleine Kreis in dem großen abrollt, nennt man Cardanische Kreise.
-
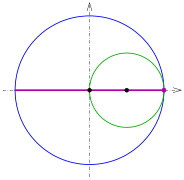
(Strecke)
-
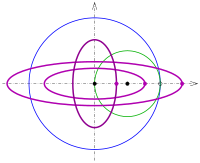
(Ellipsen)
-
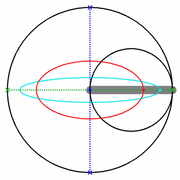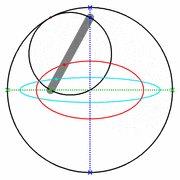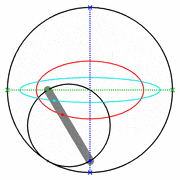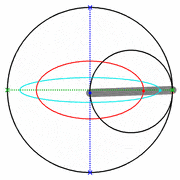 Ellipsen (rot, cyan) mit cardanischen Kreisen
Ellipsen (rot, cyan) mit cardanischen Kreisen
Literatur
- Klemens Burg, Herbert Haf, Friedrich Wille, Andreas Meister: Vektoranalysis: Höhere Mathematik für Ingenieure, Naturwissenschaftler und Mathematiker. 2. Auflage, Springer, Vieweg-Teubner, Wiesbaden 2012, ISBN 978-3-8348-8346-9.
- Mark J. Wygodski: Höhere Mathematik griffbereit: Definitionen, Theoreme, Beispiele. 2. Auflage, Vieweg, Braunschweig 1977, ISBN 3-528-18309-8.
- Matthias Richter: Grundwissen Mathematik für Ingenieure. Vieweg+Teubner, Wiesbaden 2009, ISBN 978-3-663-05772-7.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.01. 2022