
Winkel am Kreis
Für viele Fragestellungen der Elementargeometrie, bei denen es um Winkel an Kreisen geht, lassen sich die im Folgenden erklärten Begriffe und Aussagen verwenden.
Begriffe
Verbindet man die voneinander verschiedenen Endpunkte A und B eines Kreisbogens mit seinem Mittelpunkt M und einem Punkt P auf dem Kreisbogen, so liegen folgende Winkel vor:
- Umfangswinkel oder Peripheriewinkel (ϕ) nennt man einen Winkel
, dessen Scheitel P auf demjenigen Kreisbogen liegt, der den gegebenen Kreisbogen über [AB] zum vollständigen Kreis (dem Umkreis des Dreiecks ABP) ergänzt.
- Mittelpunktswinkel (μ): Ist M der Mittelpunkt des gegebenen
Kreisbogens, so bezeichnet man den Winkel
als den zugehörigen Mittelpunktswinkel (Zentriwinkel).
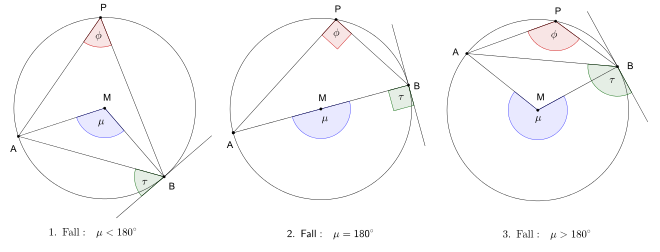
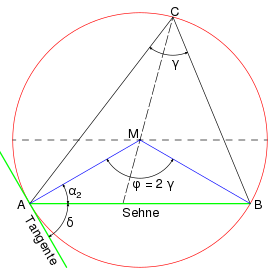
- Ein Sehnentangentenwinkel (τ) zum gegebenen Kreisbogen wird begrenzt von der Sehne [AB] und der Kreistangente im Punkt A bzw. B.
Viele Autoren von Geometrie-Lehrbüchern nehmen bei Umfangswinkeln, Mittelpunktswinkeln und Sehnentangentenwinkeln nicht Bezug auf einen gegebenen Kreisbogen, sondern auf eine gegebene Kreissehne [AB]. Legt man eine solche Definition zugrunde, so muss man zwei Arten von Umfangswinkeln unterscheiden, nämlich spitze und stumpfe Umfangswinkel. Als Mittelpunktswinkel definiert man in diesem Fall den kleineren der beiden Winkel, die von den Kreisradien [MA] und [MB] eingeschlossen werden. Die Formulierung der Sätze im nächsten Abschnitt muss bei Verwendung dieser Definition ein wenig variiert werden.
Kreiswinkelsatz (Zentriwinkelsatz)
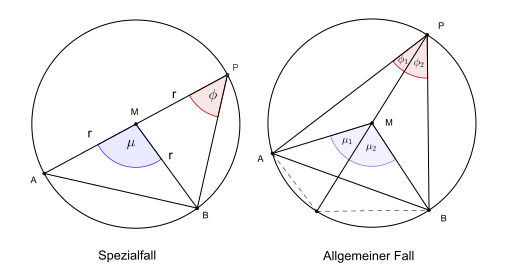
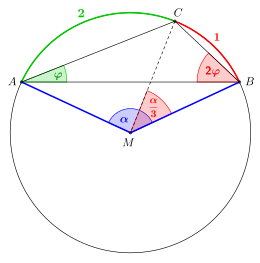
Der Mittelpunktswinkel (Zentriwinkel) eines Kreisbogens ist doppelt so groß wie einer der zugehörigen Umfangswinkel (Peripheriewinkel).
Der Beweis dieser Aussage ist in dem links skizzierten Spezialfall besonders
einfach. Die beiden Winkel bei B und P sind als Basiswinkel in dem gleichschenkligen Dreieck MBP
gleich groß. Der dritte Winkel des Dreiecks MBP (mit dem Scheitel M) hat die
Größe .
Der Satz
über die Winkelsumme ergibt folglich
und weiter, wie behauptet,
.
Im allgemeinen Fall liegt M nicht auf einem Schenkel des Umfangswinkels. Die
Gerade PM teilt dann Umfangswinkel und Mittelpunktswinkel in zwei Winkel (
und
bzw.
und
),
für die jeweils einzeln die Aussage gilt, da die Voraussetzungen des bewiesenen
Spezialfalls erfüllt sind. Deshalb gilt die Aussage auch für den gesamten
Umfangswinkel
und den gesamten Mittelpunktswinkel
.
Außerdem ermöglicht die Gültigkeit des Peripheriewinkelsatzes (siehe unten) eine
Überführung des allgemeinen Falles in den Spezialfall, ohne die Allgemeinheit
des bereits für den Spezialfall erbrachten Beweises einzuschränken.
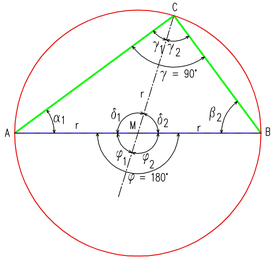
Ein besonders wichtiger Sonderfall liegt vor, wenn der gegebene Kreisbogen ein Halbkreis ist: In diesem Fall ist der Mittelpunktswinkel gleich 180° (ein gestreckter Winkel), während die Umfangswinkel gleich 90°, also rechte Winkel sind. Damit erweist sich der Satz des Thales als Spezialfall des Kreiswinkelsatzes.
Umfangswinkelsatz (Peripheriewinkelsatz)
Alle Umfangswinkel (Peripheriewinkel) über einem Kreisbogen sind gleich groß. Dieser Kreisbogen heißt dann Fasskreisbogen.
Der Umfangswinkelsatz ist eine unmittelbare Konsequenz des Kreiswinkelsatzes: Jeder Umfangswinkel ist nach dem Kreiswinkelsatz halb so groß wie der Mittelpunktswinkel (Zentriwinkel). Also müssen alle Umfangswinkel gleich groß sein.
Allerdings ist es unter Umständen notwendig, den Peripheriewinkelsatz auf anderem Wege zu beweisen, da er sonst nicht als Bedingung in der Beweisführung des Kreiswinkelsatzes verwendbar ist.
Sehnentangentenwinkelsatz
Die beiden Sehnentangentenwinkel eines Kreisbogens sind so groß wie die zugehörigen Umfangswinkel (Peripheriewinkel) und halb so groß wie der zugehörige Mittelpunktswinkel (Zentriwinkel).
Da
Zusammen mit
Anwendung bei Konstruktionsaufgaben
Umfangswinkelsatz
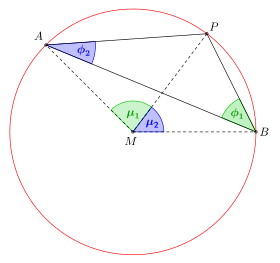
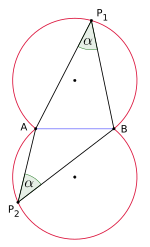
Insbesondere der Umfangswinkelsatz lässt sich nicht selten für geometrische Konstruktionen verwenden. In vielen Fällen sucht man die Menge (den geometrischen Ort) aller Punkte P, von denen aus eine gegebene Strecke (hier [AB]) unter einem bestimmten Winkel erscheint. Die gesuchte Punktmenge besteht im Allgemeinen aus zwei Kreisbögen, den sogenannten Fasskreisbögen (Bild 1).
![]() Alternativbeweis des Umfangswinkelsatzes, Landesbildungsserver
Baden-Württemberg Der hier vorgeführte Beweis besticht durch seine
Einfachheit und führt auf natürliche Weise auf die Zusammenhänge zwischen
Umfangswinkel und Mittelpunktswinkel sowie auf die Besonderheit von
Sehnenvierecken.
Alternativbeweis des Umfangswinkelsatzes, Landesbildungsserver
Baden-Württemberg Der hier vorgeführte Beweis besticht durch seine
Einfachheit und führt auf natürliche Weise auf die Zusammenhänge zwischen
Umfangswinkel und Mittelpunktswinkel sowie auf die Besonderheit von
Sehnenvierecken.
Kreiswinkelsatz
Der Kreiswinkelsatz eignet sich auch als Konstruktionsbaustein zur Lösung z.B. folgender Aufgaben:
- Zeichne ein Vierzigeck
bei dem die Seitenlänge
gegeben ist.
- Hierfür wird zuerst der Umkreis eines Zehnecks
mit nur einer Seitenlänge
konstruiert und anschließend zweimal hintereinander der Kreiswinkelsatz angewendet.
- Die Dreiteilung des Winkels mithilfe der Hyperbel; bereits im 4. Jhdt. nutzte Pappos für deren Lösung die Eigenschaften dieses Satzes (Bild 2).
Ansatz für die Dreiteilung eines beliebigen Winkels. Durch den Punkt
- Es ist aus einer vorgegebenen Seitenlänge
ein Polygon zu konstruieren, das die doppelte Anzahl Ecken eines Polygons mit gleicher Seitenlänge hat (Bild 3).
- Es ist aus einer vorgegebenen Seitenlänge
ein Polygon zu konstruieren, das die halbe Anzahl Ecken eines Polygons mit gleicher Seitenlänge hat (Bild 4).
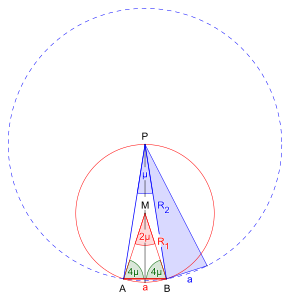
Konstruktion eines Polygons bei gegebener Seitenlänge
Beispiel:
Die Seitenlänge
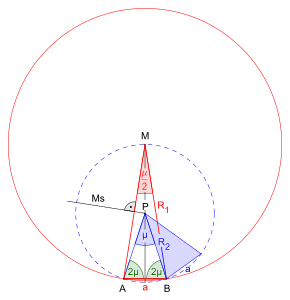
Konstruktion eines Polygons bei gegebener Seitenlänge
Beispiel:
Die Seitenlänge
Literatur
- Max Koecher, Aloys Krieg: Ebene Geometrie. 3., neu bearbeitete und erweiterte Auflage. Springer, Berlin u.a. 2007, ISBN 978-3-540-49327-3.
- Günter Aumann: Kreisgeometrie: Eine elementare Einführung. Springer, 2015, ISBN 978-3-662-45306-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 08.11. 2020