Sehne (Geometrie)
Eine Sehne einer ebenen Kurve ist eine Verbindungsstrecke zweier Punkte auf der Kurve. Sie ist also derjenige Teil einer Sekante, der zwischen den beiden Kurvenpunkten liegt.
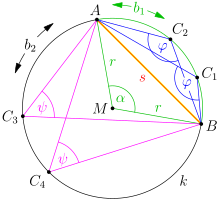
Sehne am Kreis
Die Sehne eines Kreises teilt den Kreis in zwei
in der Regel ungleich große Kreisbögen
und
,
in denen jeweils der Peripheriewinkelsatz
gilt: Alle Dreiecke mit der Sehne
als Grundseite und einem dritten Punkt
auf einem der Bögen
oder
haben im Scheitelpunkt
gleich große Winkel
bzw.
.
Verläuft die Sehne durch den Kreismittelpunkt ,
so heißt sie Durchmesser.
Der Peripheriewinkel ist dann ein rechter
Winkel (Satz
des Thales).
Für die Sehnenlänge
gilt
und wegen
sowie
und
.
Historisch wurde die Sehnenlänge mit der heute nicht mehr gebräuchlichen Winkelfunktion Chord berechnet. Früher wurde das Lot der Sehne auf den Kreismittelpunkt als Apothema bezeichnet. Die Verlängerung des Lots über die Sehne hinaus auf den Kreisrand nannte man Sagitta. Die Längen von Apothema und Sagitta ergeben zusammen den Kreisradius.
Al-Battânîs (* zw. 850 und 869, † 929) war der erste, der statt geometrischer Sehnen den Sinus gebrauchte.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.06. 2021