Sehnensatz
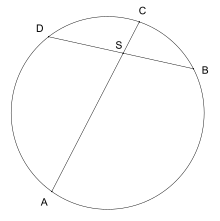
Der Sehnensatz ist ein Satz aus der Elementargeometrie und beschreibt eine Beziehung zwischen den Strecken, die von zwei sich schneidenden Kreissehnen gebildet werden.
Genauer besagt er:
- Schneiden sich in einem Kreis zwei Sehnen in einem Punkt
, so ist das Produkt der dadurch gebildeten Abschnitte auf der einen Sehne gleich dem Produkt der Abschnitte auf der anderen Sehne.
Formulierung des Satzes
Gegeben sei ein Kreis
mit zwei Sehnen,
die sich in einem Punkt
schneiden. Die Schnittpunkte
des Kreises mit der einen Sehne seien mit
und
,
die mit der anderen Sehne mit
und
bezeichnet. Dann gilt:
Die Aussage kann auch als Verhältnisgleichung formuliert werden:
Umkehrung
Es gilt auch die Umkehrung des Satzes: Wenn für die Diagonalen eines Vierecks
mit dem Diagonalenschnittpunkt
gilt:
dann besitzt dieses Viereck einen Umkreis, das heißt, es ist ein Sehnenviereck.
Zusammenhang mit dem Höhensatz
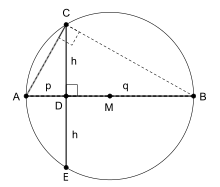
|CD||DE|=|AD||DB| <=> h2=pq
Der Sehnensatz lässt sich auch als eine Verallgemeinerung des Höhensatzes von Euklid auffassen. Wählt man die beiden Sehnen nämlich so, dass eine von ihnen dem Durchmesser entspricht und die andere auf ihr senkrecht steht, so bilden deren Endpunkte mit den Endpunkten des Durchmessers nach dem Satz des Thales ein rechtwinkliges Dreieck und die Aussage des Sehnensatzes entspricht in dieser Konfiguration der des Höhensatzes von Euklid.
Herleitung
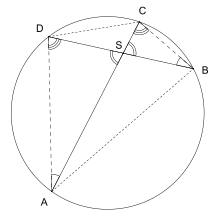
Der Satz ergibt sich unmittelbar aus in der Konfiguration auftretenden ähnlichen Dreiecken. Für die Dreiecke ASD and BSC gilt nämlich:
Damit sind die beiden Dreiecke ähnlich und es folgt somit:
Ein rechnerischer Nachweis mit Hilfe des Satzes von Vieta ist in dem Artikel Potenz (Geometrie) enthalten.
Siehe auch
- Sekantensatz
- Sekanten-Tangenten-Satz
- Potenz (Geometrie), vereinigt die Aussage von Sehnen-, Sekanten- und Sekanten-Tangentensatz in einem einheitlichen Konzept
Literatur
- Max Koecher, Aloys Krieg: Ebene Geometrie. 2. neu bearbeitete und erweiterte Auflage. Springer-Verlag, Berlin u.a. 2000, ISBN 3-540-67643-0 (Springer-Lehrbuch).
- Hans Schupp: Elementargeometrie. Schöningh, Paderborn 1977, ISBN 3-506-99189-2, (Uni-Taschenbücher 669).


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.06. 2021