Sekantensatz
Der Sekantensatz besagt: Schneiden sich zwei Sekanten
außerhalb des Kreises in einem Punkt ,
so ist das Produkt der Abschnittslängen vom Sekantenschnittpunkt bis zu den
beiden Schnittpunkten von Kreis und Sekante auf beiden Sekanten gleich groß.
Kürzer: Das Produkt der Sekantenabschnitte ist konstant.
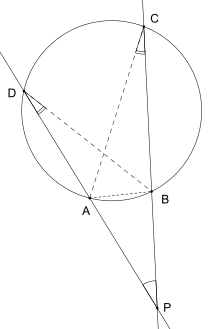
Formulierung des Satzes
Gegeben sei ein Kreis
mit zwei Sekanten, die sich in einem
Punkt
außerhalb des Kreises schneiden. Bezeichnet man die Schnittpunkte des Kreises
mit der einen Sekante als
und
und die Schnittpunkte mit der anderen Sekante als
und
,
so gilt:
Diese Aussage kann man auch als Verhältnisgleichung formulieren:
Beweisidee
Der Sekantensatz lässt sich – ähnlich wie der Sehnensatz und der Sekanten-Tangenten-Satz – mit Hilfe ähnlicher Dreiecke beweisen.
Die Dreiecke
und
sind ähnliche
Dreiecke, denn:
- Der Winkel
in Punkt
ist beiden Dreiecken gemeinsam.
- Umfangswinkel über einer
Sehne sind gleich groß. Anwendung dieses Satzes auf die Sehne
ergibt
.
Daraus ergibt sich die Verhältnisgleichung
.
Durch Multiplikation mit
erhält man:
Ein rechnerischer Nachweis mit Hilfe des Satzes von Vieta ist in dem Artikel Potenz (Geometrie) enthalten.
Siehe auch
- Sehnensatz
- Sekanten-Tangenten-Satz
- Potenz (Geometrie), vereinigt die Aussage von Sehen-, Sekenten- und Sekanten-Tangentensatz in einem einheitlichen Konzept
Literatur
- Max Koecher, Aloys Krieg: Ebene Geometrie. 2. Auflage. Springer-Verlag Berlin Heidelberg New York, 2000, ISBN 3-540-67643-0.
- H. Schupp: Elementargeometrie, UTB Schöningh (1977), ISBN 3-506-99189-2.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.06. 2021