Potenz (Geometrie)
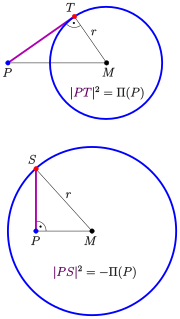
Der Begriff Potenz bezeichnet in der Geometrie
ein spezielles, von Jakob
Steiner 1826 eingeführtes Maß dafür, wie weit außerhalb oder innerhalb
eines Kreises
sich ein Punkt befindet.
Die Potenz eines Punktes
bezüglich eines Kreises
mit Mittelpunkt
und Radius
ist die reelle Zahl
Falls
außerhalb des Kreises liegt, ist >
und gleich dem Quadrat der tangentialen Distanz
von
zum Kreis
(siehe Bild). Dies folgt aus dem Satz
des Pythagoras.
Falls
auf dem Kreis liegt, ist
.
Falls
innerhalb des Kreises liegt, ist
.
Steiner benutzte die Potenz eines Kreises, um zahlreiche Aussagen über Kreise zu beweisen. Z.B. eine Konstruktion der Malfatti-Kreise.
Geometrische Bedeutung
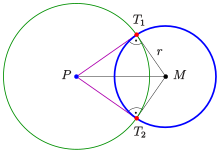
Außer den im ersten Bild mit Hilfe des Satzes von Pythagoras erkennbaren geometrischen Bedeutungen der Potenz, gibt es weitere Eigenschaften:
Orthogonalkreis
Zu einem Punkt
außerhalb des Kreises
gibt es zwei Berührpunkte
auf dem Kreis
(siehe Bild), die gleichweit von
entfernt sind. Der Kreis mit
als Mittelpunkt durch
geht also auch durch
und schneidet den Kreis
senkrecht. Dies liefert eine weitere geometrische Bedeutung der Potenz:
- Der Kreis mit Mittelpunkt
und Radius
schneidet den Kreis
senkrecht.
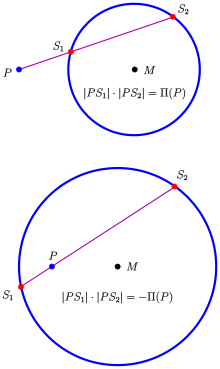
Sekantensatz, Sehnensatz
Im Sekantensatz und Sehnensatz spielt die Potenz eines Punktes die Rolle einer Invarianten:
- Sekantensatz: Liegt der Punkt
außerhalb des Kreises und sind
und
die Schnittpunkte einer beliebigen Geraden
durch
mit dem Kreis, so ist
, also unabhängig von der Gerade
. Diese Aussage ist auch dann noch richtig, wenn
und
zusammenfallen (Sekanten-Tangenten-Satz).
- Sehnensatz: Sind
und
die Schnittpunkte einer beliebigen Geraden
durch
mit dem Kreis, so ist
.
Potenzgerade
Betrachtet man zu zwei vorgegebenen Kreisen (Mittelpunkte
und Radien
),
einen Punkt
,
so hat dieser die Potenz
bezgl. des ersten Kreises und die Potenz
bezgl. des zweiten Kreises. Bestimmt man die Gesamtheit aller Punkte, die bezgl.
beider Kreise dieselbe Potenz besitzen, es ist also
,
so erhält man eine Gerade, die Potenzgerade
der beiden Kreise.
Sekantensatz, Sehnensatz: einheitlicher Beweis
Bei den Sätzen Sekantensatz, Sekanten-Tangenten-Satz und Sehnensatz spielt die Potenz eines Punktes als Invariante eine wesentliche Rolle. Diese Sätze lassen sich mit Hilfe von ähnlichen Dreiecken und dem Kreiswinkelsatz koordinatenfrei beweisen.
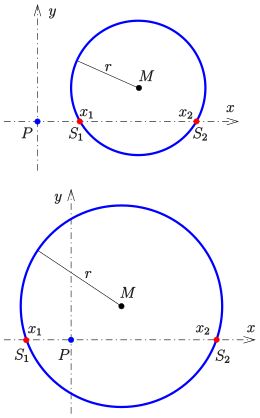
Für einen einfachen rechnerischen und einheitlichen Nachweis kann man das
Koordinatensystem so einführen, dass der Punkt ,
durch den die Sekanten/Sehnen/Tangenten gehen der Nullpunkt ist und die
jeweilige Sekante bzw. Sehne auf der x-Achse liegt. Der Kreis
hat den Mittelpunkt
und Radius
:
Die Potenz des Punktes
bezgl. des Kreises
ist
.
Die Schnittpunkte
der x-Achse (Gerade
)
mit dem Kreis ergeben sich aus der quadratischen Gleichung
Nach dem Satz von Vieta gilt für die möglichen Lösungen:
.
Also gilt (siehe Bild)
, falls
außerhalb des Kreises liegt,
, falls
innerhalb des Kreises liegt (
haben dann verschiedene Vorzeichen und
ist negativ !).
In beiden Fällen hängt also das Produkt
nur von
ab und nicht von den mit
kollinearen
Punkten
.
Der erste Fall liefert den Sekantensatz, der zweite Fall den Sehnensatz.
Ist im ersten Fall die x-Achse eine Tangente (d.h. ),
so ist
das Quadrat der tangentialen Distanz des Punktes
zum Kreis
und liefert die Aussage des Sekanten-Tangenten-Satzes.
Potenz bezüglich einer Kugel
Das Konzept der Potenz eines Punktes bezüglich eines Kreises lässt sich auf Kugeln im Raum übertragen. Auch die Sekanten/Sehnen-Sätze haben im Raum ihre Gültigkeit. Analog zur Potenzgerade zweier Kreise gibt es im Raum eine Potenzebene zu zwei Kugeln. Zu drei Kugeln gibt es eine dem Radikal dreier Kreise entsprechende Potenzgerade.
- Nachweis der Sekanten/Sehnen-Sätze im Raum
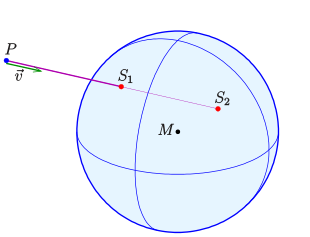
Es sei
ein Punkt,
eine Kugel mit Mittelpunkt im Ursprung und
ein Einheitsvektor. Die Parameter
der möglichen Schnittpunkte der Gerade
(durch
)
mit der Kugel
ergeben sich durch Einsetzen der Parameterdarstellung der Gerade in die
Kugelgleichung:
Aus dem Satz von Vieta folgt für die Lösungen dieser quadratischen Gleichung:
. (Unabhängig von
!)
ist die Potenz von
bezüglich der Kugel
.
Da
ist, gilt für die Schnittpunkte
:
, falls
außerhalb der Kugel liegt,
, falls
innerhalb der Kugel liegt (
haben verschiedene Vorzeichen !).
Im Fall
ist die Gerade eine Tangente und die Potenz
das Quadrat des tangentialen Abstandes von
zur Kugel
.
Dieser vektorielle Beweis lässt sich formal auch auf den ebenen Fall (Kreis) anwenden.
Literatur
- Jakob Steiner: Einige geometrische Betrachtungen. In: Journal für die reine und angewandte Mathematik, Band 1, 1826, S. 161–184
- Jacob Steiner, C.F. Geiser, H. Schröter: Jacob Steiner’s Vorlesungen über synthetische Geometrie. Erster Theil: Die Theorie der Kegelschnitte in elementarer Darstellung. Teubner, 1867.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.06. 2021