Nephroide

Konstruktion einer Nephroide durch Abrollen eines Kreises auf einem Kreis mit doppeltem Radius

Konstruktion derselben Nephroide durch Abrollen eines Kreises um einen Kreis mit 2/3 Radius

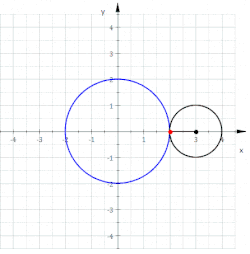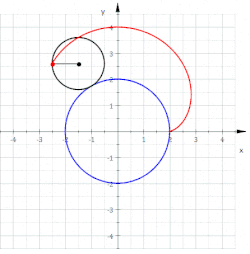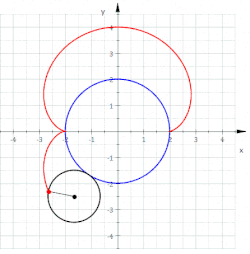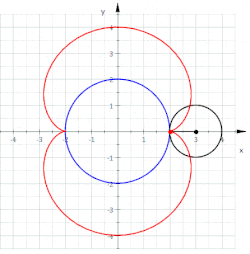
Eine Nephroide (aus altgriechisch ὁ νεφρός ho nephros, „die Niere“, nach ihrer Gestalt) ist eine algebraische Kurve 6. Grades. Die Nephroide entsteht durch Abrollen eines Kreises mit dem Radius auf der Außenseite eines Kreises mit dem Radius . Damit gehört die Nephroide in die Klasse der Epizykloiden.

Gleichungen einer Nephroide

Nephroide: Definition

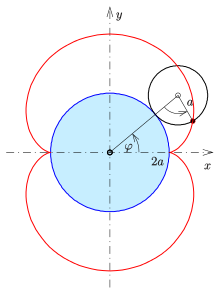
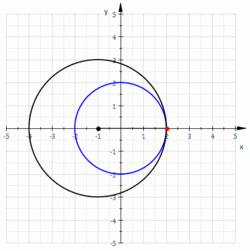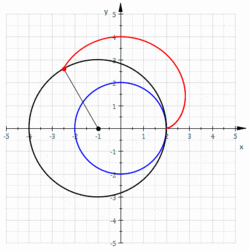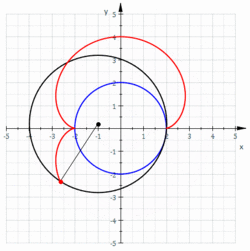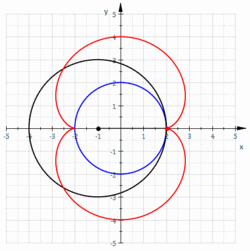
Ist der Radius des kleinen (rollenden) Kreises und $(0,0),\;2a$ der Mittelpunkt und Radius des großen (festen) Kreises, $2\varphi$ der Rollwinkel (des kleinen Kreises) und der Punkt $(2a,0)$ der Startpunkt (s. Bild), so erhält man die

Parameterdarstellung:

$x(\varphi )=3a\cos \varphi -a\cos 3\varphi =6a\cos \varphi -4a\cos ^{3}\varphi \ ,$

$y(\varphi )=3a\sin \varphi -a\sin 3\varphi =4a\sin ^{3}\varphi \ ,\qquad 0\leq \varphi <2\pi$ .

Einsetzen der Parameterdarstellung in die Gleichung

$(x^{2}+y^{2}-4a^{2})^{3}=108a^{4}y^{2}.$

beweist, dass sie die zugehörige implizite Darstellung ist.

Beweis der Parameterdarstellung

Der Beweis der Parameterdarstellung lässt sich mit Hilfe komplexer Zahlen und ihre Darstellung als Gaußsche Zahlenebene leicht führen. Die Rollbewegung des schwarzen Kreises auf dem blauen Kreis kann man in die Hintereinanderausführung zweier Drehungen zerlegen. Die Drehung eines Punktes (komplexe Zahl) um den Nullpunkt $0$ mit dem Winkel $\varphi$ wird durch die Multiplikation mit $e^{i\varphi }$ bewirkt.

Die Drehung $\Phi_3$ um den Punkt $3a$ um den Winkel $2\varphi$ ist $z\mapsto 3a+(z-3a)e^{i2\varphi }$ .

Die Drehung $\Phi_0$ um den Punkt $0$ um den Winkel $\varphi$ ist $z\mapsto ze^{i\varphi }$ .

Ein Nephroidenpunkt $p(\varphi )$ entsteht durch Drehung des Punktes mit $\Phi_3$ und anschließende Drehung mit $\Phi_0$ :

$p(\varphi )=\Phi _{0}(\Phi _{3}(2a))=\Phi _{0}(3a-ae^{i2\varphi })=(3a-ae^{i2\varphi })e^{i\varphi }=3ae^{i\varphi }-ae^{i3\varphi }$ .

Hieraus ergibt sich

${\begin{array}{cclcccc}x(\varphi )&=&3a\cos \varphi -a\cos 3\varphi &=&6a\cos \varphi -4a\cos ^{3}\varphi \ ,&&\\y(\varphi )&=&3a\sin \varphi -a\sin 3\varphi &=&4a\sin ^{3}\varphi &.&\end{array}}$

(Es wurden die Formeln $e^{i\varphi }=\cos \varphi +i\sin \varphi ,\ \cos ^{2}\varphi +\sin ^{2}\varphi =1,\ \cos 3\varphi =4\cos ^{3}\varphi -3\cos \varphi ,\;\sin 3\varphi =3\sin \varphi -4\sin ^{3}\varphi$ benutzt. Siehe Formelsammlung Trigonometrie.)

Beweis der impliziten Darstellung

Mit $x^{2}+y^{2}-4a^{2}=(3a\cos \varphi -a\cos 3\varphi )^{2}+(3a\sin \varphi -a\sin 3\varphi )^{2}-4a^{2}=\cdots =6a^{2}(1-\cos 2\varphi )=12a^{2}\sin ^{2}\varphi$ ergibt sich

$(x^{2}+y^{2}-4a^{2})^{3}=(12a^{2})^{3}\sin ^{6}\varphi =108a^{4}(4a\sin ^{3}\varphi )^{2}=108a^{4}y^{2}\ .$

andere Orientierung

Falls die Spitzen auf der y-Achse liegen:
Parameterdarstellung:

$x=3a\cos \varphi +a\cos 3\varphi ,\quad y=3a\sin \varphi +a\sin 3\varphi ).$

Gleichung:

$(x^{2}+y^{2}-4a^{2})^{3}=108a^{4}x^{2}.$

Eine verkürzte Nephroide

Flächeninhalt, Kurvenlänge und Krümmungsradius

Für die obige Nephroide ist

die Kurvenlänge $L=24a$ , und
der Flächeninhalt $A=12\pi a^{2}\ .$
der Krümmungsradius $\rho (\varphi )=|3a\sin \varphi |.$

Die Beweise verwenden die Parameterdarstellung

$x(\varphi )=6a\cos \varphi -4a\cos ^{3}\varphi \ ,$

$y(\varphi )=4a\sin ^{3}\varphi$

der obigen Nephroide und ihre Ableitungen

${\dot {x}}=-6a\sin \varphi (1-2\cos ^{2}\varphi )\ ,\quad \ {\ddot {x}}=-6a\cos \varphi (5-6\cos ^{2}\varphi )\ ,$

${\dot {y}}=12a\sin ^{2}\varphi \cos \varphi \quad ,\quad \quad \quad \quad {\ddot {y}}=12a\sin \varphi (3\cos ^{2}\varphi -1)\ .$

Formeln für den Flächeninhalt und die Kurvenlänge findet man z.B. hier.

Beweis für die Kurvenlänge

Mit der Formel für die Länge einer parametrisierten Kurve ergibt sich

$L=2\int _{0}^{\pi }{\sqrt {{\dot {x}}^{2}+{\dot {y}}^{2}}}\;d\varphi =\cdots =12a\int _{0}^{\pi }\sin \varphi \;d\varphi =24a$ .

Beweis für den Flächeninhalt (mit der Leibniz-Sektorformel): $A=2\cdot {\tfrac {1}{2}}|\int _{0}^{\pi }[x{\dot {y}}-y{\dot {x}}]\;d\varphi |=\cdots =24a^{2}\int _{0}^{\pi }\sin ^{2}\varphi \;d\varphi =12\pi a^{2}$ .

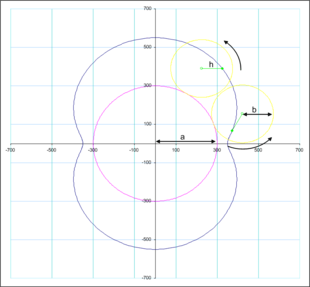
Beweis für den Krümmungsradius: $\rho =\left|{\frac {\left({{\dot {x}}^{2}+{\dot {y}}^{2}}\right)^{\frac {3}{2}}}{{\dot {x}}{\ddot {y}}-{\dot {y}}{\ddot {x}}}}\right|=\cdots =|3a\sin \varphi |.$

Nephroide als Einhüllende einer Kreisschar

Es gilt:

Ist $k_{0}$ ein Kreis und $D_{1}D_{2}$ Punkte eines Durchmessers $d_{12}$ , so ist die Einhüllende der Schar von Kreisen, deren Mittelpunkte auf $k_{0}$ liegen und den Durchmesser $d_{12}$ berühren, eine Nephroide mit den Spitzen $D_{1},D_{2}$ .

Beweis

Es sei $k_{0}$ der Kreis $(2a\cos \varphi ,2a\sin \varphi )$ mit dem Mittelpunkt (0,0) und dem Radius . Der nötige Durchmesser liege auf der x-Achse (s. Bild). Die Kreisschar ist:

$f(x,y,\varphi )=(x-2a\cos \varphi )^{2}+(y-2a\sin \varphi )^{2}-(2a\sin \varphi )^{2}=0\ .$

Die Einhüllendenbedingung ist

$f_{\varphi }(x,y,\varphi )=2a(x\sin \varphi -y\cos \varphi -2a\cos \varphi \sin \varphi )=0\ .$

Man rechnet nach, dass der Nephroidenpunkt $p(\varphi )=(6a\cos \varphi -4a\cos ^{3}\varphi \;,\;4a\sin ^{3}\varphi )$ die beiden Gleichungen $f(x,y,\varphi )=0,\;f_{\varphi }(x,y,\varphi )=0$ erfüllt und damit ein Punkt der Einhüllenden der Kreisschar ist.

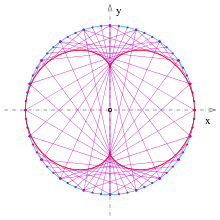
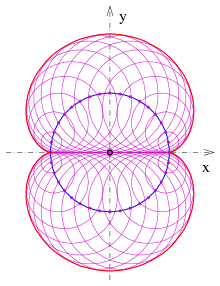
Nephroide als Einhüllende einer Geradenschar: Die Tangenten der Nephroide sind Sehnen eines Kreises. Die Sehnen verlaufen jeweils zwischen Punkt n und Punkt 3n auf der Kreisbahn, die gleichmäßig in einer Anzahl von Schritten unterteilt ist, die einem Vielfachem von 3 entspricht.

Nephroide als Einhüllende einer Geradenschar: Die Tangenten der Nephroide sind Sehnen eines Kreises

Nephroide als Einhüllende einer Geradenschar

Ähnlich der Erzeugung einer Kardioide als Einhüllende einer Geradenschar gilt hier:

Zeichne einen Kreis, unterteile ihn gleichmäßig mit Punkten (s. Bild) und nummeriere diese fortlaufend.
Zeichne die Sehnen: $(1,3),(2,6),....,(n,3n),....,(N,3N),(N+1,3),(N+2,6),....,$ . (Man kann es so ausdrücken: Der zweite Punkt der Sehne bewegt sich mit dreifacher Geschwindigkeit.)
Die Einhüllende dieser Strecken ist eine Nephroide.

Beweis

Im Folgenden werden die trigonometrischen Formeln für $\cos \alpha +\cos \beta ,\ \sin \alpha +\sin \beta ,\ \cos(\alpha +\beta ),\ \cos 2\alpha$ verwendet. Um die Rechnungen einfach zu halten, wird der Beweis für die Nephroide mit den Spitzen auf der y-Achse geführt.

Gleichung der Tangente: an die Nephroide mit der Parameterdarstellung; $x=3\cos \varphi +\cos 3\varphi ,\;y=3\sin \varphi +\sin 3\varphi$ :

Aus der Parameterdarstellung berechnet man zunächst den Normalenvektoren ${\vec {n}}=({\dot {y}},-{\dot {x}})^{T}$ .
Die Gleichung der Tangente ${\dot {y}}(\varphi )\cdot (x-x(\varphi ))-{\dot {x}}(\varphi )\cdot (y-y(\varphi ))=0$ ist dann:

$(\cos 2\varphi \cdot x\ +\ \sin 2\varphi \cdot y)\cos \varphi =4\cos ^{2}\varphi \ .$

Für $\varphi ={\tfrac {\pi }{2}},{\tfrac {3\pi }{2}}$ hat die Nephroide ihre Spitzen, wo sie keine Tangente besitzt. Für $\varphi \neq {\tfrac {\pi }{2}},{\tfrac {3\pi }{2}}$ kann man durch $\cos \varphi$ dividieren und erhält schließlich

$\cos 2\varphi \cdot x+\sin 2\varphi \cdot y=4\cos \varphi \ .$

Gleichung der Sekante: an den Kreis mit Mittelpunkt und Radius : Für die Gleichung der Sekante durch die beiden Punkte $(4\cos \theta ,4\sin \theta ),\ (4\cos {\color {red}3}\theta ,4\sin {\color {red}3}\theta ))$ ergibt sich:; $(\cos 2\theta \cdot x+\sin 2\theta \cdot y)\sin \theta =4\cos \theta \sin \theta \ .$

Für $\theta =0,\pi$ artet die Sekante zu einem Punkt aus. Für $\theta \neq 0\pi$ kann man durch $\sin \theta$ dividieren und es ergibt sich die Gleichung der Sekante:

$\cos 2\theta \cdot x+\sin 2\theta \cdot y=4\cos \theta \ .$

Die beiden Winkel $\varphi ,\theta$ haben zwar verschiedene Bedeutungen ( $\varphi$ ist der halbe Rollwinkel, $\theta$ ist der Parameter des Kreises, dessen Sekanten berechnet werden), für $\varphi =\theta$ ergibt sich aber dieselbe Gerade. Also ist auch jede obige Sekante an den Kreis eine Tangente der Nephroide und

die Nephroide ist die Einhüllende der Kreissehnen.

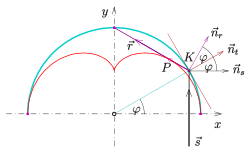
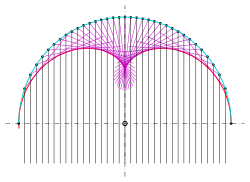
Nephroide als Kaustik eines Kreises: Prinzip

Nephroide als Kaustik eines Halbkreises

Die vorigen Überlegungen liefern auch einen Beweis dafür, dass als Kaustik eines Halbkreises eine Nephroide auftritt:

Fallen in der Ebene parallele Lichtstrahlen in einen spiegelnden Halbkreis gemäß der Abbildung, so sind die reflektierten Lichtstrahlen die Tangenten einer Nephroide. (s. Abschnitt: Nephroide im täglichen Leben)

Beweis

Der Kreis habe (wie im vorigen Abschnitt) den Nullpunkt als Mittelpunkt und sein Radius sei . Der Kreis hat dann die Parameterdarstellung

$k(\varphi )=4(\cos \varphi ,\sin \varphi )\ .$

Die Tangente im Kreispunkt $K=k(\varphi )$ hat den Normalenvektor ${\vec {n}}_{t}=(\cos \varphi ,\sin \varphi )^{T}$ . Der reflektierte Strahl muss dann (laut Abbildung) den Normalenvektor ${\vec {n}}_{r}=(\cos {\color {red}2}\varphi ,\sin {\color {red}2}\varphi )^{T}$ haben und durch den Kreispunkt $K:4(\cos \varphi ,\sin \varphi )$ gehen. Der reflektierte Strahl liegt also auf der Gerade mit der Gleichung

$\cos {\color {red}2}\varphi \cdot x\ +\ \sin {\color {red}2}\varphi \cdot y=4\cos \varphi \ ,$

die wiederum die Tangente an die Nephroide des vorigen Abschnitts im Punkt

$P:(3\cos \varphi +\cos 3\varphi ,3\sin \varphi +\sin 3\varphi )$

ist (s. oben).

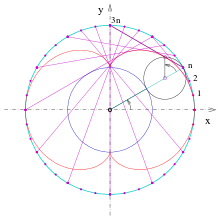
Evolute einer Nephroide

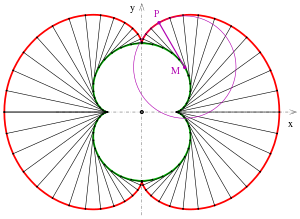
Nephroide (rot) und ihre Evolute (grün),
magenta: ein Punkt P, sein Krümmungsmittelpunkt M und der zugehörige Krümmungskreis

Die Evolute einer ebenen Kurve ist der geometrische Ort aller Krümmungsmittelpunkte dieser Kurve. Für eine parametrisierte Kurve ${\vec {x}}(s)={\vec {c}}(s)$ mit Krümmungsradius $\rho (s)$ hat die Evolute die Parameterdarstellung

${\vec {X}}(s)={\vec {c}}(s)+\rho (s){\vec {n}}(s).$

wobei ${\vec n}(s)$ die geeignet orientierte Einheitsnormale ist. ( ${\vec n}(s)$ zeigt zu dem Krümmungsmittelpunkt hin.)

Für eine Nephroide im Bild gilt:

Die Evolute einer Nephroide ist wieder eine Nephroide, halb so groß.

Beweis

Die Nephroide im Bild (die Spitzen liegen auf der y-Achse !) hat die Parameterdarstellung

$x=3\cos \varphi +\cos 3\varphi ,\quad y=3\sin \varphi +\sin 3\varphi \ ,$

ist die Einheitsnormale

${\vec {n}}(\varphi )=(-\cos 2\varphi ,-\sin 2\varphi )^{T}$ (s. oben)

und hat den Krümmungsradius (s. oben)

$\rho (\varphi )=3\cos \varphi$ .

Also hat die Evolute die Parameterdarstellung

$x=3\cos \varphi +\cos 3\varphi -3\cos \varphi \cdot \cos 2\varphi =\cdots =3\cos \varphi -2\cos ^{3}\varphi ,$

$y=3\sin \varphi +\sin 3\varphi -3\cos \varphi \cdot \sin 2\varphi \ =\cdots =2\sin ^{3}\varphi \ ,$

Diese Gleichungen beschreiben eine Nephroide, die halb so groß und um 90 Grad gedreht ist (s. Bild und den Abschnitt Gleichungen einer Nephroide).

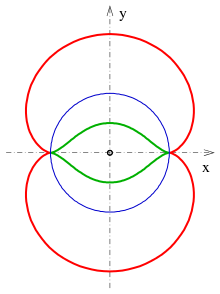
Inversion (grün) einer Nephroide (rot) am blauen Kreis

Inversion (Kreisspiegelung) einer Nephroide

Die Spiegelung

$x\mapsto {\frac {4a^{2}x}{x^{2}+y^{2}}},\quad y\mapsto {\frac {4a^{2}y}{x^{2}+y^{2}}}$

am Kreis mit Mittelpunkt (0,0) und Radius bildet die Nephroide mit der Gleichung

$(x^{2}+y^{2}-4a^{2})^{3}=108a^{4}y^{2}$

auf die Kurve 6. Grades mit der Gleichung

$(4a^{2}-(x^{2}+y^{2}))^{3}=27a^{2}(x^{2}+y^{2})y^{2}$

ab (siehe Bild).

Nephroide im täglichen Leben

Fällt Licht einer unendlich weit entfernten Lichtquelle seitlich auf eine konkave, kreisförmige reflektierende Oberfläche, so bildet die Einhüllende der Lichtstrahlen einen Teil einer Nephroide. Manchmal wird sie daher auch „Kaffeetassenkaustik“ (Kaustik = Brennlinie) genannt. Man kann sie auch auf der Straße beobachten, wenn die blanken Felgen eines Fahrrades das Licht auf den Boden reflektieren: Da das Sonnenlicht den Zylindermantel der Fahrradfelge parallel trifft, bildet sich eine Brennfläche, deren Profil die Form einer halben Nephroide hat und die, wenn man sich leicht in die Kurve legt, mit dem ebenen Untergrund einen Teil einer Nephroide als Schnittfigur bildet.

Siehe auch

Kardioide

Literatur

Kurt Meyberg, Peter Vachenauer: Höhere Mathematik 1. Springer-Verlag, 1995, ISBN 3-540-59188-5.

Basierend auf einem Artikel in:

Wikipedia.de