Konchoide

Die Konchoide (die „Muschelähnliche“ – wie lat. concha von griech. κόγχη bzw. κόγχος, Muschel) ist eine spezielle ebene Kurve. Sie beschreibt die Bewegung eines Punktes, der – von einem festen Punkt (Pol) aus gesehen – zu einer gegebenen Kurve konstanten Abstand einhält.

Eigentliche Konchoide

Sie war schon im antiken Griechenland bekannt und wird nach Nikomedes als Konchoide von Nikomedes bezeichnet. Ein anderer Name ist Muschelkurve. Der Name leitet sich daher ab, dass der Graph den zwei Schalen einer Muschel ähnelt.

Drei Typen der Konchoide des Nikomedes

Kartesische Koordinaten: $(x-a)^{2}(x^{2}+y^{2})-b^{2}x^{2}\,=\,0$

Polarkoordinaten: $r={\frac {a}{\cos \varphi }}\pm b$

Parameterdarstellung: $x(\varphi )=a+b\cos \varphi ;\qquad y(\varphi )=a\tan \varphi +b\sin \varphi$

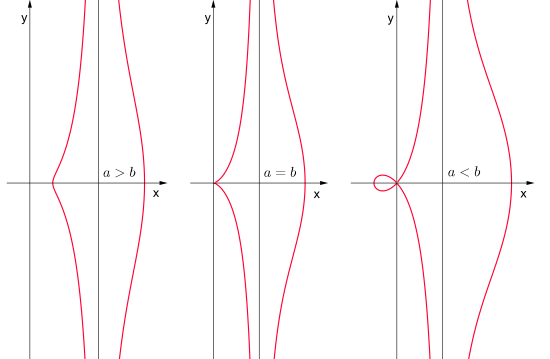
Eigenschaften

Die Punkte der Konchoide des Nikomedes sind gekennzeichnet durch die folgende geometrische Eigenschaft: Gegeben seien eine Gerade g ("Leitgerade"), ein Punkt A, der von g den Abstand a hat (mit a > 0), und eine reelle Zahl b (mit b > 0). Dann liegen für einen beliebigen Punkt B der Geraden g die beiden Punkte P und P', die auf der Geraden AB liegen und von B die Entfernung b haben, auf der Konchoide.

Konstruktion der Konchoide

Die Fälle sind ein Typ der Kurven, die mit dem Trivialnamen Hundekurve bezeichnet werden, insbesondere für ähnelt der eine Ast der eigentlichen Traktrix.

Im Folgenden wird jeweils vorausgesetzt, dass die Koordinatenachsen so liegen wie in der Skizze, also der Pol im Ursprung liegt.

Die Konchoide des Nikomedes ist achsensymmetrisch bezüglich der x-Achse. Im Allgemeinen liegen drei Kurvenpunkte auf der Symmetrieachse, nämlich , und der Ursprung.
- Für ist der Ursprung ein isolierter Punkt.
- Für fallen zwei der drei Punkte im Ursprung zusammen, für ist der Ursprung ein Doppelpunkt der Kurve, wird also zweimal durchlaufen, der Graph hat eine Schleife.
  - Die beiden Tangenten im Ursprung haben die Gleichungen

$y={\frac {{\sqrt {b^{2}-a^{2}}}}{a}}x$ und $y=-{\frac {{\sqrt {b^{2}-a^{2}}}}{a}}x$ .

Für

fallen beide Tangenten mit der x-Achse zusammen. Der Ursprung ist also eine eigentliche Spitze

Gewöhnliche Konchoide

Der Begriff der Konchoide lässt sich verallgemeinern:

Gegeben seien eine Kurve k (Leitkurve), ein Punkt A (Pol) und eine positive reelle Zahl b. Zu jedem beliebigen Punkt B, der auf der Kurve k liegt, betrachtet man nun die beiden Punkte, die auf der Geraden AB liegen und von B die Entfernung b haben. Die Menge aller dieser Punkte bezeichnet man als die Konchoide der Leitkurve.

Die einfachste Darstellung benutzt Polarkoordinaten: Liegt A im Ursprung, und sei $r=f(\varphi )$ , dann lautet die Gleichung der gewöhnlichen Konchoide:
$r=f(\varphi )\pm b$

Eigenschaften

Alle gewöhnlichen Konchoiden sind Zissoiden, wobei die eine Kurve ein Kreis im Ursprung ist.

Eine Pascalsche Schnecke ist eine Konchoide, wobei die gegebene Kurve ein Kreis ist.

Allgemeine Konchoide

Erweitert man die Bildungsregel, indem man den Abstand b nicht entlang der Geraden AB aufträgt, sondern entlang einer Geraden, die im Punkt B einen konstanten Winkel $\alpha$ zu AB hat, erhält man die allgemeine Konchoide. Im Falle $\alpha =0$ und $\alpha =\pi$ ergibt sich die gewöhnliche Konchoide, anderenfalls spricht man von einer schiefen Konchoide.

Konchoidenverzahnung in der Getriebetechnik

In der Getriebetechnik ist die sogenannte Konchoidenverzahnung eine von mehreren Techniken zur Verzahnung von Zahnrädern und Zahnstangen.

Anmerkungen

Die sogenannte Konchoide von de Sluze ist tatsächlich eine spezielle Zissoide.
Die sogenannte Konchoide von Dürer ist eine allgemeinere Konstruktion.

Basierend auf einem Artikel in:

Wikipedia.de