Evolvente

Zwei Evolventen (rot) einer Parabel

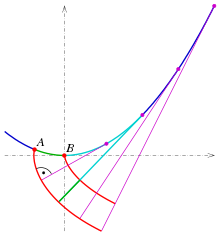
Die Evolvente (auch Involute) ist ein Begriff aus dem mathematischen Teilgebiet Differentialgeometrie. Jeder rektifizierbaren Kurve wird eine Schar von anderen Kurven als deren Evolventen zugeordnet, die durch die „Abwicklung“ von deren Tangente entstehen.

Anschaulich lässt sich die Evolvente als Fadenlinie darstellen: Ein flacher Körper, dessen eine Seitenfläche die Form der Ausgangskurve hat, wird auf ein Blatt Papier gelegt. Über die Ausgangskurve ist ein dünner Faden gewickelt und straff gespannt. Am äußeren Ende des Fadens wird ein Stift befestigt, dessen Spitze auf dem Papier aufliegt. Dann wird der Faden langsam von der Kurve abgewickelt, wobei er stets straff gehalten wird. Die Kurve, die auf dem Papier entsteht, ist eine Evolvente.

Da der Faden anfangs eine beliebige Länge haben kann, gibt es zu jeder Kurve unendlich viele Evolventen, die alle parallel zueinander verlaufen, das heißt: Sind zwei Evolventen gegeben, so ist jede Normale der einen auch Normale der anderen, und alle diese Normalen sind zwischen den beiden Evolventen gleich lang. Jede Normale einer Evolvente ist also Normale aller Evolventen. Die Normalen der Evolventen sind einfach die Tangenten der gegebenen Kurve. Diese ist Hüllkurve (Enveloppe) der Evolventennormalen. Meist ist mit Evolvente die Kreisevolvente gemeint; dies ist jedoch nur ein Spezialfall der allgemeinen Evolvente.

Evolvente einer parametrisierten Kurve

Beschreibt ${\vec {x}}={\vec {c}}(t),\;t\in [t_{1},t_{2}]$ eine reguläre Kurve in der euklidischen Ebene, deren Krümmung nirgends 0 ist, und ist $a\in (t_{1},t_{2})$ , so ist die zugehörige Kurve mit der Parameterdarstellung

${\vec {X}}={\vec {C}}_{a}(t)={\vec {c}}(t)-{\frac {{\vec {c}}'(t)}{|{\vec {c}}'(t)|}}\;\int _{a}^{t}|{\vec {c}}'(w)|\;\mathrm {d} w$

eine Evolvente der gegebenen Kurve.
Das Integral beschreibt die akute Länge des abgewickelten Fadens der Kurve in dem Intervall $[a,t]$ und der Vektor davor ist der Tangenteneinheitsvektor. Addiert man zu dem Integral eine beliebige, aber feste Zahl l_0 , so erhält man eine Evolvente mit einem um l_0 längeren Faden. Also: Nicht nur mit dem Parameter kann man die Fadenlänge und damit die Evolventen variieren, sondern auch durch Addition einer Zahl l_0 zu dem Integral (s. Beispiel Neilsche Parabel).

Ist ${\vec {x}}={\vec {c}}(t)=(x(t),y(t))^{T}$ , so ist

${\begin{aligned}X(t)&=x(t)-{\frac {x'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(w)^{2}+y'(w)^{2}}}\,\mathrm {d} w\\Y(t)&=y(t)-{\frac {y'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(w)^{2}+y'(w)^{2}}}\,\mathrm {d} w\;.\end{aligned}}$

Eigenschaften der Evolventen

Evolvente: Eigenschaften

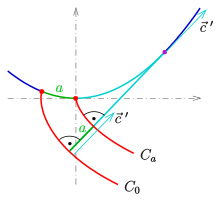
Um Eigenschaften einer regulären Kurve herzuleiten, ist es vorteilhaft, die Bogenlänge der gegebenen Kurve als Parameter zu verwenden. Denn dann gilt $\;|{\vec {c}}'(s)|=1\;$ und $\;{\vec {c}}''(s)=\kappa (s){\vec {n}}(s)\;$ , wobei $\kappa$ die Krümmung und ${\vec {n}}$ die Einheitsnormale ist. Für die Evolvente ergibt sich:

${\vec {C}}_{a}(s)={\vec {c}}(s)-{\vec {c}}'(s)(s-a)\;$ und

${\vec {C}}_{a}'(s)=-{\vec {c}}''(s)(s-a)=-\kappa (s){\vec {n}}(s)(s-a)\;.$

Hieraus folgt:

Die Evolvente ist im Punkt ${\vec {C}}_{a}(a)$ nicht regulär (es ist $|{\vec {C}}_{a}'(a)|=0$ ),

und aus $\;{\vec {C}}_{a}'(s)\cdot {\vec {c}}'(s)=0\;$ folgt:

Die Normale der Evolvente im Punkt ${\vec {C}}_{a}(s)$ ist Tangente der gegebenen Kurve im Punkt ${\vec {c}}(s)$ und
die Evolventen sind parallele Kurven, da ${\vec {C}}_{a}(s)={\vec {C}}_{0}(s)+a{\vec {c}}'(s)$ und ${\vec {c}}'(s)$ die Einheitsnormale in ${\vec {C}}_{0}(s)$ ist.

Die letzte Eigenschaft legt die folgende Strategie zur Bestimmung der Evolventen einer Kurve nahe:

Verwende eine Parameterdarstellung der gegebenen Kurve, die eine möglichst einfache Stammfunktion des zu lösenden Integrals zulässt.
Überlege, für welchen Anfangsparameter und/oder welche Fadenverlängerung das Integral einfach wird.
Findet man auf diese Weise eine einfach zu beschreibende Evolvente, so ergeben sich alle Evolventen als Parallelkurven davon.

Beispiele

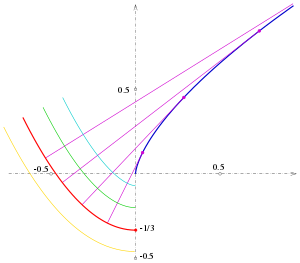
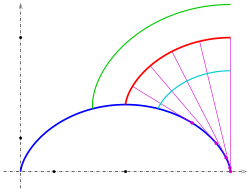
Evolventen eines Kreises

→ Hauptartikel: Kreisevolvente

Für den Kreis mit der Parameterdarstellung $\;(r\cos(t),r\sin(t))\;$ ist ${\vec {c}}'(t)=(-r\sin t,r\cos t)^{T}$ und damit $|{\vec {c}}'(t)|=r$ . Das Integral hat den Wert $r(t-a)$ . Also sind die Gleichungen der Evolvente:

$X(t)=r(\cos t+(t-a)\sin t)$

$Y(t)=r(\sin t-(t-a)\cos t)$

In der Zeichnung sind die Evolventen für $a=-0{,}5$ (grün), a=0 (rot), $a=0{,}5$ (magenta) und a=1 (cyan) gezeichnet. Die Evolventen sind ähnlich einer archimedischen Spirale, sie sind aber keine.

Für die Bogenlänge der Evolvente mit $0\leq t\leq t_{2}$ ergibt sich

$L={\frac {r}{2}}{t_{2}}^{2}\;.$

Evolventen einer Neilschen Parabel

Evolventen einer neilschen Parabel (blau). Nur die rote Kurve ist eine Parabel.

Die Parameterdarstellung $\;{\vec {c}}(t)=({\tfrac {t^{3}}{3}},{\tfrac {t^{2}}{2}})^{T}\;$ beschreibt eine Neilsche Parabel. Wegen $\;{\vec {c}}'(t)=(t^{2},t)^{T}\;$ ist $\;|{\vec {c}}'(t)|=t{\sqrt {t^{2}+1}}$ und $\int _{0}^{t}w{\sqrt {w^{2}+1}}\;\mathrm {d} w={\frac {1}{3}}{\sqrt {t^{2}+1}}^{3}-1/3$ . Verlängert man den Faden um $l_{0}=1/3$ wird die Rechnung einfach und es ergibt sich

$X(t)=\;\cdots \;=-{\frac {t}{3}}$

$Y(t)=\;\cdots \;={\frac {t^{2}}{6}}-{\frac {1}{3}}\ .$

Elimination des Parameters liefert die Parabel mit der Gleichung $\;Y={\frac {3}{2}}X^{2}-{\frac {1}{3}}\;.$
Also:

Die Evolventen der Neilschen Parabel $\;({\tfrac {t^{3}}{3}},{\tfrac {t^{2}}{2}})\;$ sind Parallelkurven der Parabel $\;y={\frac {3}{2}}x^{2}-{\frac {1}{3}}\;.$

(Man beachte: Die Parallelkurven einer Parabel sind keine Parabeln mehr!)

Bemerkung: Berechnet man die Evolute der Parabel $\;y={\frac {3}{2}}x^{2}-{\frac {1}{3}}\;$ , so ergibt sich wieder die Neilsche Parabel $\;({\tfrac {t^{3}}{3}},{\tfrac {t^{2}}{2}})\;$ (s. Abschnitt Evolvente und Evolute.)

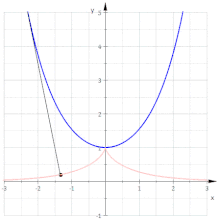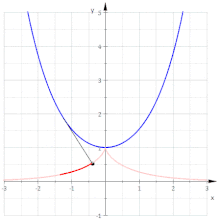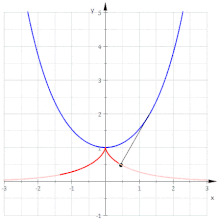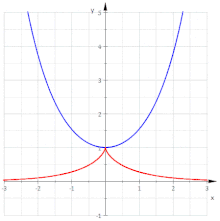
Die rote Evolvente einer Kettenlinie (blau) ist eine Traktrix.

Evolventen der Kettenlinie

Für die Kettenlinie $\;(t,\cosh t)\;$ ergibt sich $\;{\vec {c}}'(t)=(1,\sinh t)^{T}\;$ und wegen $\;\cosh ^{2}t-\sinh ^{2}t=1\;$ ist $\;|{\vec {c}}'(t)|=\cosh t$ und $\;\int _{0}^{t}\cdots =\sinh t\;.$ Damit ergibt sich die Parameterdarstellung der Evolvente:

$(t-\tanh t,1/\cosh t)\;.$

Dies ist die Parameterdarstellung einer Traktrix. Es gilt:

Die Evolventen der Kettenlinie $\;(t,\cosh t)\;$ sind Parallelkurven der Traktrix $(t-\tanh t,1/\cosh t)\;.$

Evolventen einer Zykloide

Evolventen einer Zykloide (blau): Nur die rote Kurve ist wieder eine Zykloide.

Die Parameterdarstellung $\;{\vec {c}}(t)=(t-\sin t,1-\cos t)^{T}\;$ beschreibt eine Zykloide. Wegen $\;{\vec {c}}'(t)=(1-\cos t,\sin t)^{T}\;$ ist $\;|{\vec {c}}'(t)|=\cdots =2\sin {\frac {t}{2}}$ und $\int _{\pi }^{t}2\sin {\frac {w}{2}}\;\mathrm {d} w=-4\cos {\frac {t}{2}}$ . (Es wurden einige trigonometrische Formeln verwendet.)
Es ergibt sich

$X(t)=\;\cdots \;=t+\sin t$

$Y(t)=\;\cdots \;=3+\cos t\ .$

Diese Gleichungen beschreiben die im Bild (rot) gezeigte verschobene Zykloide.
Also gilt:

Die Evolventen der Zykloide $\;(t-\sin t,1-\cos t)\;$ sind Parallelkurven der Zykloide

$(t+\sin t,3+\cos t)\;.$

Evolvente und Evolute

Die Evolute einer gegebenen Kurve $k_{0}$ besteht aus den Krümmungsmittelpunkten von $k_{0}$ . Die Verbindung zwischen Evolute und Evolvente besteht in folgendem Zusammenhang:

Jede Kurve ist die Evolute jeder ihrer Evolventen.

Wegen dieser Wechselbeziehung wird die Evolvente zuweilen auch Involute genannt.

Anwendungen

Technik

In der Technik hat die Evolvente besonders bei der Konstruktion von Zahnrädern und Zahnstangen eine große Bedeutung. Bei der häufig angewandten Evolventenverzahnung ist der Querschnitt einer Zahnflanke Teil einer Kreisevolvente. Dadurch wird gewährleistet, dass sich im Eingriff stehende Zähne entlang einer geraden Eingriffslinie (der Tangente an die Grundkreise) berühren. Die Evolventenform ist dabei einfacher zu fertigen als die ebenfalls verwendete Zykloidenform der Zahnflanke.

Medizin

Auch im Bereich der Medizin findet sich der Begriff wieder. So haben die Evolvente der spiralig gekrümmten Femurcondylen im Kniegelenk und deren daher auf der resultierenden Evolute zu findende Schnittpunkte der transversalen Bewegungsachsen ihre Bedeutung im Verständnis der Biomechanik des Knies und kniespezifischer Gelenkseigenschaften.

Sport

In der Leichtathletik werden die Startlinien auf einer 400-Meter-Bahn mit Hilfe der Evolvente berechnet, damit Läufer auf den Außenbahnen dieselbe Strecke zurücklegen wie Läufer auf den weiter innen liegenden Bahnen. Dies gilt insbesondere für den 200- und 400-Meter-Lauf, die Sprintstaffeln sowie die Langstreckenwettbewerbe.

Literatur

K. Burg, H. Haf, F. Wille, A. Meister: Vektoranalysis: Höhere Mathematik für Ingenieure, Naturwissenschaftler und … Springer-Verlag, 2012, ISBN 3834883468.
Kleine Enzyklopädie Mathematik. Harry Deutsch Verlag, 1977, ISBN 3 87144 323 9.

Basierend auf einem Artikel in:

Wikipedia.de