Möbius-Ebene

Eine Möbius-Ebene, benannt nach August Ferdinand Möbius, ist im klassischen Fall eine Inzidenzstruktur, die im Wesentlichen die Geometrie der Geraden und Kreise in der reellen Anschauungsebene beschreibt: Eine Gerade ist durch 2 Punkte, ein Kreis durch 3 Punkte eindeutig bestimmt. Eine Gerade oder Kreis schneidet/berührt einen Kreis in 0, 1 oder 2 Punkten. Um die besondere Rolle der Geraden aufzuheben, fügt man jeder Geraden einen gemeinsamen neuen Punkt $\infty$ hinzu und nennt Kreise und die so erweiterten Geraden Zykel. Die neue Inzidenzstruktur hat jetzt die einfacheren Eigenschaften:

Möbius-Ebene: Berührrelation (A2)

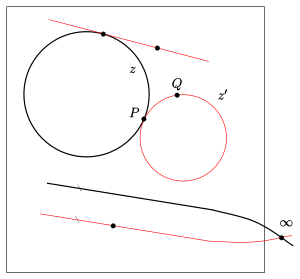
(A1): Zu je 3 Punkten gibt es genau einen Zykel , der diese enthält. (Liegen die Punkte auf einer Geraden , so ist die um $\infty$ erweiterte Gerade der gesuchte Zykel, liegen sie nicht auf einer Geraden, so gibt es genau einen Kreis durch .)
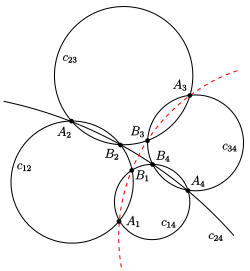
(A2): Zu einem Zykel , einem Punkt auf und einem Punkt nicht auf gibt es genau einen Zykel $z^{\prime }$ durch und , der in berührt. (Um diese Eigenschaft nachzuweisen, muss man die verschiedenen Möglichkeiten für durchspielen, was allerdings ohne Mühe möglich ist (s. Bild).)

Es ist aber nicht zu erwarten, dass die hier beschriebene Geometrie der erweiterten Geraden und Kreise die einzige Inzidenzstruktur ist, die die Eigenschaften (A1), (A2) besitzt. Ersetzt man die reellen Zahlen durch die rationalen Zahlen $\mathbb {Q}$ , so bleiben (A1), (A2) gültig. Allerdings geht die Gültigkeit von (A1), (A2) bei Verwendung der komplexen Zahlen (statt der reellen) verloren. Das heißt, nur die Verwendung gewisser Zahlkörper (s.u.) erhält die Eigenschaften (A1), (A2).

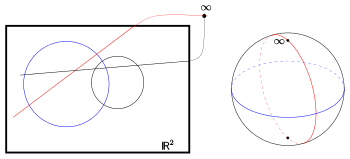
Neben dem formal inhomogenen Modell (es gibt Geraden und Kreise) erhält man mit Hilfe der Umkehrung einer geeigneten stereografischen Projektion ein homogenes räumliches Modell: Die Punkte der neuen Inzidenzstruktur sind die Punkte auf der Kugeloberfläche und die Zykel sind die Kreise auf der Kugel. Die klassische reelle Möbius-Ebene kann also auch als die Geometrie der ebenen Schnitte (Kreise) auf einer Kugel aufgefasst werden. Der Nachweis von (A1) und (A2) verlangt im räumlichen Modell keine lästigen Fallunterscheidungen.

Eine Möbius-Ebene ist eine der drei Benz-Ebenen: Möbius-Ebene, Laguerre-Ebene und Minkowski-Ebene. Die klassische Laguerre-Ebene ist die Geometrie der Parabeln und die klassische Minkowski-Ebene die Geometrie der Hyperbeln.

Die Axiome einer Möbius-Ebene

Aufgrund der Inzidenzeigenschaften (A1), (A2) der klassischen reellen Möbius-Ebene definiert man:

Möbius-Ebene: Axiome (A1), (A2)

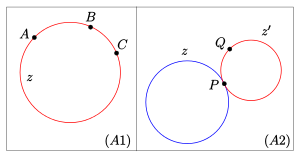
Eine Inzidenzstruktur ${\mathfrak M}=({{\mathcal P}},{{\mathcal Z}},\in )$ mit der Menge der Punkte ${{\mathcal P}}$ und der Menge der Zykeln ${{\mathcal Z}}$ heißt Möbius-Ebene, wenn die folgenden Axiome erfüllt sind:

(A1): Zu je 3 Punkten A,B,C

gibt es genau einen Zykel , der A,B,C

enthält.

(A2): (Berühraxiom) Zu einem beliebigen Zykel und zwei beliebigen Punkten $P\in z$ , $Q\notin z$ gibt es genau einen Zykel durch P,Q,

der in berührt, d.h. mit $z\cap z'=\{P\}$ .

(A3): Jeder Zykel enthält wenigstens 3 Punkte. Es gibt wenigstens einen Zykel.

Vier Punkte A,B,C,D heißen konzyklisch, wenn es einen Zykel gibt, der A,B,C,D enthält.

Möbius-Ebene: Minimalmodell (nur die Zykel durch $\infty$ sind gezeichnet. Je 3 Punkte bilden einen Zykel.)

Wie oben schon erwähnt, erfüllt nicht nur die klassische reelle Möbius-Ebene die Axiome (A1), (A2), (A3). Es gibt sehr viele Beispiele von Möbius-Ebenen, die vom klassischen Modell verschieden sind (s.u.). Ähnlich zum Minimalmodell einer affinen oder projektiven Ebene gibt es auch ein Minimalmodell einer Möbius-Ebene. Es besteht aus 5 Punkten:

${\mathcal {P}}:=\{A,B,C,D,\infty \},\quad {\mathcal {Z}}:=\{z\mid z\subset {\mathcal {P}},|z|=3\}$

Also ist $|{\mathcal {Z}}|={5 \choose 3}=10$ .

Die enge Beziehung der klassischen Möbius-Ebene zur reellen affinen Ebene ist auch zwischen dem Minimalmodell einer Möbius-Ebene und dem Minimalmodell einer affinen Ebene zu erkennen. Diese enge Beziehung ist sogar typisch für Möbius-Ebenen:

Für eine Möbius-Ebene ${\mathfrak M}=({{\mathcal P}},{{\mathcal Z}},\in )$ und $P\in {{\mathcal P}}$ definieren wir die Inzidenzstruktur ${{\mathfrak A}}_{P}:=({{\mathcal P}}\setminus \{P\},\{z\setminus \{P\}|P\in z\in {{\mathcal Z}}\},\in )$ und nennen sie Ableitung im Punkt P.

Beim klassischen Modell ist die Ableitung ${\mathfrak {A}}_{\infty }$ am Punkt $\infty$ die zugrunde liegende reelle affine Ebene (s.u.). Die große Bedeutung einer Ableitung in einem Punkt besteht in der leicht zu beweisenden Aussage:

Jede Ableitung einer Möbius-Ebene ist eine affine Ebene.

Diese Eigenschaft erlaubt die Verwendung vieler Resultate über affine Ebenen und ist auch der Grund für eine alternative Definition einer Möbius-Ebene:

Satz: Eine Inzidenzstruktur $({{\mathcal P}},{{\mathcal Z}},\in )$ ist genau dann eine Möbius-Ebene, wenn gilt:

A’: Für jeden Punkt $P\in {{\mathcal P}}$ ist die Ableitung ${{\mathfrak A}}_{P}$ eine affine Ebene.

Für endliche Möbius-Ebenen, d.h. $|{{\mathcal P}}|<\infty$ , gilt (ähnlich wie bei affinen Ebenen):

Je zwei Zykel enthalten dieselbe Anzahl von Punkten.

Diese Eigenschaft gibt Anlass zur folgenden Definition:

Für eine endliche Möbius-Ebene ${\mathfrak M}=({{\mathcal P}},{{\mathcal Z}},\in )$ und einen Zykel $z\in {{\mathcal Z}}$ heißt die natürliche Zahl die Ordnung von ${\mathfrak {M}}$ .

Aus kombinatorischen Überlegungen ergibt sich:

Für eine endliche Möbius-Ebene ${\mathfrak M}=({{\mathcal P}},{{\mathcal Z}},\in )$ der Ordnung gilt:

a) Jede Ableitung ${{\mathfrak A}}_{P}$ ist eine affine Ebene der Ordnung

b) $|{\mathcal {P}}|=n^{2}+1$

c) $|{\mathcal {Z}}|=n(n^{2}+1)$

Die klassische reelle Möbius-Ebene

Klassische Möbius-Ebene: 2d/3d-Modell

Wir gehen von der reellen affine Ebene ${\mathfrak {A}}(\mathbb{R} )$ aus und erhalten mit der quadratischen Form $\rho (x,y)=x^{2}+y^{2}$ die reelle Euklidische Ebene: $\mathbb {R} ^{2}$ ist die Menge der Punkte, Geraden werden durch Gleichungen y=mx+b oder x=c beschrieben und ein Kreis ist eine Punktmenge, die eine Gleichung

$\rho (x-x_{0},y-y_{0})=(x-x_{0})^{2}+(y-y_{0})^{2}=r^{2},\ r>0$

erfüllt.

Die Geometrie der Geraden und Kreise kann homogenisiert werden (ähnlich der Erweiterung einer affinen Ebene zu einer projektiven Ebene), indem man sie einbettet in die Inzidenzstruktur $({{\mathcal P}},{{\mathcal Z}},\in )$ mit

${{\mathcal P}}:=\mathbb{R} ^{2}\cup \{\infty \},\infty \notin \mathbb{R}$ als Menge der Punkte und

${\mathcal {Z}}:=\{g\cup \{\infty \}\mid g{\text{ Gerade von }}{\mathfrak {A}}(\mathbb {R} )\}\cup \{k\mid k{\text{ Kreis von }}{\mathfrak {A}}(\mathbb {R} )\}$ als Menge der Zykel.

$({{\mathcal P}},{{\mathcal Z}},\in )$ heißt die klassische reelle Möbius-Ebene.

Innerhalb der neuen Inzidenzstruktur spielen die erweiterten Geraden geometrisch keine Sonderrolle mehr und $({{\mathcal P}},{{\mathcal Z}},\in )$ erfüllt die Axiome (A1) und (A2).

Die übliche Beschreibung der reellen Ebene durch komplexe Zahlen (z bezeichnet jetzt keine Zykel!)

$z=x+iy\ \leftrightarrow \ (x,y)\in \mathbb{R} ^{2}$

liefert die folgende Beschreibung von $({{\mathcal P}},{{\mathcal Z}},\in )$ ( $\overline {z}=x-iy$ ist die zu konjugiert komplexe Zahl):

${\mathcal {P}}:=\mathbb {C} \cup \{\infty \}$

${\mathcal {Z}}:=\{\{z\in \mathbb {C} \mid az+{\overline {az}}+b=0\}\ \cup \ \{\infty \}\mid 0\neq a\in \mathbb {C} ,b\in \mathbb {R} \}\ \cup \ \{\{z\in \mathbb {C} \mid (z-z_{0}){\overline {(z-z_{0})}}=d\}\mid z_{0}\in \mathbb {C} ,d\in \mathbb {R} ,d>0\}$

Der große Vorteil dieser Beschreibung ist die einfache Möglichkeit, Automorphismen (Permutationen von ${{\mathcal P}}$ , die Zykel auf Zykel abbilden) anzugeben. Die folgenden Abbildungen sind Automorphismen von $({\mathcal {P}},{\mathcal {Z}},\in ):$

(1) $\ z\mapsto rz,\ \infty \mapsto \infty ,\$ mit $r\in \mathbb {C} \$ (Drehstreckung)

(2) $\ z\mapsto z+s,\ \infty \mapsto \infty ,\$ mit $s\in \mathbb {C} \$ (Translation)

(3) $\ z\mapsto \displaystyle {\tfrac {1}{z}},\ z\neq 0,\ 0\mapsto \infty ,\ \infty \mapsto 0\$ (Spiegelung an $\pm 1$ )

(4) $\ z\mapsto {\overline {z}},\ \infty \mapsto \infty \$ (Spiegelung an der reellen Achse)

Betrachtet man $\mathbb {C} \cup \{\infty \}$ als die projektive Gerade über den komplexen Zahlen $\mathbb {C}$ , so erkennt man, dass die Abbildungen (1)–(3) die Gruppe $PGL(2,\mathbb {C} )$ der Möbiustransformationen erzeugen. Die Geometrie $({{\mathcal P}},{{\mathcal Z}},\in )$ ist also eine sehr homogene Struktur. Z.B. kann man die reelle Achse mit einem Automorphismus auf jeden anderen Zykel abbilden. Zusammen mit der Abbildung (4) ergibt sich:

An jedem Zykel gibt es eine Spiegelung, auch Inversion genannt. Zum Beispiel: $z\mapsto 1/{\overline {z}}$ ist die Inversion am Einheitskreis $z{\overline {z}}=1$ . Diese Eigenschaft begründet den in der englischen Literatur gebräuchlichen Namen inversive plane.

Stereografische Projektion

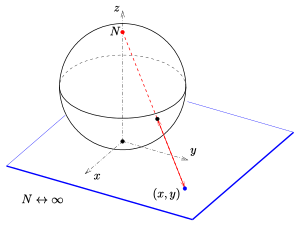
Ähnlich dem räumlichen Modell einer projektiven Ebene gibt es auch ein räumliches Modell der klassischen Möbius-Ebene $({{\mathcal P}},{{\mathcal Z}},\in )$ , das den formalen Unterschied zwischen Kreisen und erweiterten Geraden aufhebt: Die Geometrie $({{\mathcal P}},{{\mathcal Z}},\in )$ ist isomorph zur Geometrie der Kreise auf einer Kugel. Den zugehörigen Isomorphismus vermittelt eine geeignete stereografische Projektion. Zum Beispiel:

$\Phi :(x,y)\mapsto \left({\frac {x}{1+x^{2}+y^{2}}},{\frac {y}{1+x^{2}+y^{2}}},{\frac {x^{2}+y^{2}}{1+x^{2}+y^{2}}}\right)=(u,v,w)$

$\Phi$ projiziert vom Punkt (0,0,1) aus

die x-y-Ebene auf die Kugel mit der Gleichung $u^{2}+v^{2}+w^{2}-w=0$ . Diese Kugel hat den Mittelpunkt $(0,0,{\tfrac {1}{2}})$ und den Radius $r={\tfrac {1}{2}}$ .
den Kreis mit der Gleichung $x^{2}+y^{2}-ax-by-c=0$ in die Ebene . D.h., das Bild des Kreises ist ein ebener Schnitt mit der Kugel und damit wieder ein Kreis (auf der Kugel). Die Abbildung $\Phi$ ist also kreistreu. Die Kreisebenen gehen alle nicht durch das Projektionszentrum .
die Gerade in die Ebene . D.h., eine Gerade wird auf einen um den Punkt verminderten Kugelkreis in einer Ebene durch das Projektionszentrum abgebildet.

Für die Umkehrabbildung (von der in N punktierten Kugel auf die x-y-Ebene) gilt:

$\Phi ^{-1}:(u,v,w)\mapsto ({\frac {u}{1-w}},{\frac {v}{1-w}})=(x,y)$

Miquelsche Möbius-Ebenen

Bei der Suche nach weiteren Beispielen einer Möbius-Ebene lohnt es sich, das klassische Modell zu verallgemeinern: Wir gehen von einer affinen Ebene ${\mathfrak A}(K)$ über einem Körper und einer geeigneten quadratischen Form $\rho$ auf ${\mathfrak A}(K)$ aus, um Kreise zu definieren. Aber einfach die reellen Zahlen $\mathbb {R}$ durch einen beliebigen Körper zu ersetzen und die klassische quadratische Form $x^{2}+y^{2}$ zur Beschreibung der Kreise beizuhalten, funktioniert nicht immer. Nur für geeignete Paare von Körpern und quadratischen Formen erhält man Möbius-Ebenen ${\mathfrak M}(K,\rho )$ . Diese sind (wie das klassische Modell) durch eine große Homogenität (viele Automorphismen) und den folgenden Satz von Miquel ausgezeichnet.

Satz von Miquel

Satz (MIQUEL):

Für eine Möbius-Ebene ${\mathfrak M}(K,\rho )$ gilt:

Wenn für beliebige 8 Punkte $P_{1},\ldots ,P_{8}$ , die so den Ecken eines Würfels zugeordnet werden können, dass 4 Punkte zu 5 Seitenflächen jeweils auf einem Kreis liegen, so ist dies auch für die 4 Punkte der 6. Seitenfläche der Fall (s. Bild).

Die Stärke dieser Schließungsfigur zeigt sich in der Gültigkeit der Umkehrung des Satzes von Miquel:

Satz (CHEN):

Nur Möbius-Ebenen der Form ${\mathfrak M}(K,\rho )$ erfüllen den Satz von Miquel.

Aufgrund des letzten Satzes nennt man eine Möbius-Ebene ${\mathfrak {M}}(K,\rho )$ miquelsch.

Bemerkung: Das Minimalmodell einer Möbius-Ebene ist miquelsch. Es ist isomorph zur Möbius-Ebene

${\mathfrak {M}}(K,\rho )$ mit $K=GF(2)$ (Körper $\{0,1\}$ ) und $\rho (x,y)=x^{2}+xy+y^{2}.$

(Z.B. beschreibt $x^{2}+xy+y^{2}=1$ die Punktmenge $\{(0,1),(1,0),(1,1)\}$ .)

Bemerkung:

Im Fall $K=\mathbb{R}$ ist auch $\rho (x,y)=x^{2}+2y^{2}$ geeignet. Die „Kreise“ sind hier Ellipsen.

Im Fall $K={\mathbb {Q}}$ (der Körper der rationalen Zahlen) ist $\rho (x,y)=x^{2}+y^{2}$ geeignet.

Im Fall $K={\mathbb {Q}}$ ist auch $\rho (x,y)=x^{2}-2y^{2}$ geeignet.

Ist $K=\mathbb {C}$ der Körper der komplexen Zahlen, so gibt es überhaupt keine geeignete quadratische Form.

Bemerkung:

Eine stereografische Projektion zeigt: ${\mathfrak {M}}(K,\rho )$ ist isomorph zur Geometrie der ebenen Schnitte einer Kugel (projektive Quadrik vom Index 1) im 3-dimensionalen projektiven Raum über dem Körper
Eine miquelsche Möbius-Ebene ${\mathfrak {M}}(K,\rho )$ lässt sich, analog zum klassischen reellen Fall, immer als projektive Gerade über einem Erweiterungskörper von beschreiben.

Bemerkung: Im klassischen Fall lässt sich der Satz von Miquel mit elementaren Mitteln (Kreisviereck) beweisen, s. Satz von Miquel.

Ovoidale Möbius-Ebenen

Möbius-Ebene: Büschelsatz

Es gibt viele Möbius-Ebenen, die nicht miquelsch sind. Eine große Klasse von Möbius-Ebenen, die die miquelschen enthält, bilden die ovoidalen Möbius-Ebenen. Eine ovoidale Möbius-Ebene ist die Geometrie der ebenen Schnitte auf einem Ovoid. Ein Ovoid ist eine quadratische Menge und besitzt dieselben geometrischen Eigenschaften wie eine Kugel im reellen 3-dimensionalen Raum: 1) Eine Gerade trifft ein Ovoid in 0, 1 oder 2 Punkten. 2) Die Menge der Tangenten in einem Punkt überdeckt eine Ebene (die Tangentialebene in diesem Punkt). Im reellen 3-dimensionalen Raum kann man z.B. eine Halbkugel in geeigneter Weise glatt mit einer Hälfte eines Ellipsoids verkleben, um ein Ovoid zu erhalten, das keine Quadrik ist. Selbst im endlichen Fall gibt es Ovoide, die keine Quadriken sind (s. quadratische Menge). Für die Klasse der ovoidalen Möbius-Ebenen gibt es einen dem Satz von Miquel ähnlichen Schließungssatz, den Büschelsatz (engl.: Bundle Theorem). Er charakterisiert die ovoidalen Möbius-Ebenen. Der Satz von Miquel und der Büschelsatz haben für Möbius-Ebenen eine ähnliche Bedeutung wie die Sätze von Pappos und Desargues für projektive Ebenen.

Klassifikation der Möbiusebenen

1965 publizierte Christoph Hering eine zur Klassifikation der projektiven Ebenen analoge Klassifikation der Möbiusebenen, die auf der Reichhaltigkeit der jeweiligen Automorphismengruppe beruht.

Literatur

W. Benz: Vorlesungen über Geometrie der Algebren. Springer, 1973,
Albrecht Beutelspacher: Einführung in die endliche Geometrie. Bd. 2: Projektive Räume. Bibliographisches Institut, Mannheim u.a. 1983, ISBN 3-411-01648-5.

Basierend auf einem Artikel in:

Wikipedia.de