
Minkowski-Ebene
Eine Minkowski-Ebene, benannt nach Hermann
Minkowski, ist im klassischen Fall eine Inzidenzstruktur,
die im Wesentlichen die Geometrie der durch eine Gleichung der Form
gegebenen Hyperbeln
und der Geraden
in der reellen Anschauungsebene beschreibt. Punkte mit denselben x- oder
y-Koordinaten haben keine Verbindung, man nennt sie deshalb (+)-parallel bzw.
(-)-parallel.
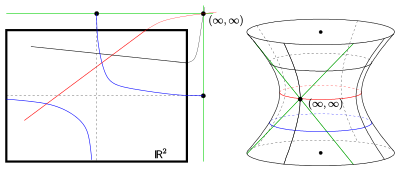
Offensichtlich gilt: Durch 3 paarweise nicht parallele Punkte geht genau eine
Hyperbel. Allerdings: Eine Gerade ist schon durch 2 Punkte eindeutig bestimmt.
Zwei Hyperbeln können sich in 2 Punkten schneiden oder in einem Punkt berühren
(gemeinsame Tangente) oder meiden. Wie bei Möbius-
und Laguerre-Ebenen
erhält man einfachere geometrische Verhältnisse, wenn man die Geometrie der
Hyperbeln/Geraden durch Hinzunahme von weiteren Punkten homogenisiert: Einer
Hyperbel
fügt man die zwei Punkte
und einer Gerade
den Punkt
hinzu und nennt die so erweiterten Hyperbel/Geraden Zykel (s. Bild). Die
neue Inzidenzstruktur hat jetzt ähnliche Eigenschaften wie eine Möbius- oder
Laguerre-Ebene (s. Abschnitt Axiome) und besitzt (auch wie Möbius- und
Laguerre-Ebenen) ein räumliches Modell: Die klassische Minkowski-Ebene ist
isomorph zur Geometrie der ebenen Schnitte eines einschaligen
Hyperboloids (s. Bild) im reellen projektiven
Raum. Ein einschaliges Hyperboloid ist eine Quadrik, die Geraden und nicht
ausgeartete projektive
Kegelschnitte enthält.
Neben diesen geometrischen Modellen der klassischen reellen Minkowski-Ebene
gibt es noch die Darstellung über dem Ring
der anormal-komplexen
Zahlen (analog der Beschreibung
der klassischen Möbius-Ebene über den komplexen Zahlen).
Eine anormal-komplexe Zahl hat (wie eine komplexe
Zahl) die Form
aber mit
.
Eine Minkowski-Ebene ist eine der 3 Benz-Ebenen: Möbius-Ebene, Laguerre-Ebene und Minkowski-Ebene. Die klassische Möbius-Ebene ist die Geometrie der Kreise und die klassische Laguerre-Ebene die Geometrie der Parabeln.
Der Name Minkowski-Ebene rührt von der Minkowski-Metrik her, mit der man pseudoeuklidische "Kreise" (Hyperbeln) beschreibt.
Die Axiome einer Minkowski-Ebene
Es sei
eine Inzidenzstruktur mit der Menge
der Punkte, der Menge
der Zykel und zwei Äquivalenzrelationen
((+)-parallel) und
((-)-parallel) auf der Menge der Punkte
.
Für einen Punkt
definieren wir:
und
.
Eine Äquivalenzklasse
oder
heißt (+)-Erzeugende bzw. (-)-Erzeugende. (Im räumlichen Modell
der klassischen Minkowski-Ebene ist eine Erzeugende eine Gerade auf dem
Hyperboloid.)
Zwei Punkte
heißen parallel (
),
falls
oder
gilt.
Eine Inzidenzstruktur
heißt Minkowski-Ebene, wenn die folgenden Axiome gelten:
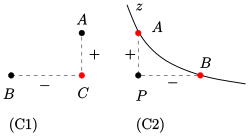

- (C1): Zu je zwei nicht parallelen Punkten
gibt es genau einen Punkt
mit
.
- (C2): Für jeden Punkt
und jeden Zykel
gibt es genau zwei Punkte
.
- (C3): Zu je 3 paarweise nicht parallelen Punkten
gibt es genau einen Zykel
, der
enthält.
- (C4):(Berühraxiom) Für jeden Zykel
, jeden Punkt
und jedem Punkt
und
gibt es genau einen Zykel
so, dass
, d.h.
berührt
im Punkt
.
- (C5): Jeder Zykel enthält wenigstens 3 Punkte. Es gibt wenigstens
einen Zykel
und einen Punkt
nicht auf
.
Für Untersuchungen einer Minkowski-Ebene sind die folgenden zu (C1) bzw. (C2) äquivalenten Aussagen von Vorteil.
- (C1'): Für je zwei Punkte
gilt:
.
- (C2'): Für jeden Punkt
und jeden Zykel
gilt:
.
Analog zu Möbius- und Laguerre-Ebenen sind auch hier die folgenden lokalen Strukturen affine Ebenen.
Für eine Minkowski-Ebene
und
definieren wir
und nennen diese Inzidenzstruktur Ableitung
im Punkt .
Bei der klassischen reellen Minkowski-Ebene ist
die reelle affine Ebene
(s. 1. Bild).
Eine direkte Konsequenz der Axiome (C1) - (C4) und (C1'), (C2') ist:
Satz: Für eine Minkowski-Ebene
ist jede Ableitung eine affine Ebene.
Hieraus ergibt sich die alternative Definition
Satz: Es sei
eine Inzidenzstruktur mit zwei Äquivalenzrelationen
und
auf der Menge der Punkte
.
ist eine Minkowski-Ebene genau dann, wenn für jeden Punkt
die Ableitung
eine affine Ebene ist.
Das Minimalmodell
Das Minimalmodell einer Minkowski-Ebene lässt sich über der Menge
von 3 Elementen definieren:
,
genau dann, wenn
und
genau dann, wenn
ist.
Also: Die Anzahl der Punkte ist
und die der Zykel
.
Für endliche Minkowski-Ebenen ergibt sich aus (C1'), (C2'):
- Es sei
eine endliche Minkowski-Ebene, d.h.
. Für jedes Paar
von Zykeln und jedes Paar
von Erzeugenden gilt:
.
Dies gibt Anlass zu folgender Definition:
Für eine endliche
Minkowski-Ebene
und einen Zykel
von
nennen wir die natürliche Zahl
die Ordnung von
.
Einfache kombinatorische Überlegungen ergeben:
- Für eine endliche Minkowski-Ebene
gilt:
- a) Jede Ableitung (affine Ebene) hat die Ordnung
.
- b)
c)
.
Die klassische reelle Minkowski-Ebene
Die formale Definition der klassischen reellen Minkowski-Ebene präzisiert die in der Einleitung beschriebene Homogenisierung der Geometrie der Hyperbeln:
, die Menge der Punkte,
-
die Menge der Zykel..
-
Die Inzidenzstruktur
heißt klassische reelle Minkowski-Ebene.
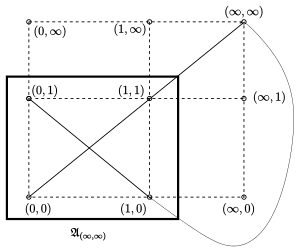
Die Menge der Punkte besteht aus ,
zwei Kopien von
und dem Punkt
.
Jede Gerade
wird durch den Punkt
,
jede Hyperbel
durch die zwei Punkte
ergänzt (s. 1. Bild).
Zwei Punkte
können genau dann nicht durch einen Zykel verbunden werden, wenn
oder
ist. Wir definieren:
Zwei Punkte
sind (+)-parallel (
),
wenn
ist, und (-)-parallel (
),
wenn
gilt.
Beide Relationen sind Äquivalenzrelationen
auf der Menge der Punkte.
Zwei Punkte
heißen parallel (
),
wenn
oder
gilt.
- Die hier definierte Inzidenzstruktur
erfüllt die Axiome einer Minkowski-Ebene.
Wie die klassische Möbius- bzw. Laguerre-Ebene gibt es auch für die klassische reelle Minkowski-Ebene ein räumliches Modell. Allerdings genügt eine affine Quadrik zur Beschreibung nicht:
- Die klassische Minkowski-Ebene ist isomorph zur Geometrie der ebenen Schnitte eines einschaligen Hyperboloids im 3-dimensionalen reellen projektiven Raum.
Miquelsche Minkowski-Ebenen
Die wichtigsten nicht klassischen Minkowski-Ebenen erhält man durch die
einfache Ersetzung der reellen Zahlen im klassischen Modell durch einen
beliebigen Körper
.
Die so erhaltene Inzidenzstruktur
ist für jeden Körper eine Minkowski-Ebene. Analog zu Möbius- und Laguerre-Ebenen
werden sie durch die entsprechende Version des Satzes von Miquel
charakterisiert:

Satz(MIQUEL):
Für eine Minkowski-Ebene
gilt:
- Wenn für beliebige 8 Punkte paarweise nicht parallele Punkte
, die so den Ecken eines Würfels zu geordnet werden können, dass 4 Punkte zu 5 Seitenflächen jeweils auf einem Zykel liegen, so ist dies auch für die 4 Punkte der 6. Seitenfläche der Fall (s. Bild: Für eine bessere Übersicht wurden Kreise statt Hyperbeln gezeichnet).
Die Bedeutung des Satzes von Miquel zeigt der folgende Satz von Chen:
Satz(CHEN):
Nur eine Minkowski-Ebene
erfüllt den Satz von Miquel.
Aufgrund dieses Satzes heißt
eine miquelsche Minkowski-Ebene.
Bemerkung: Das Minimalmodell einer Minkowski-Ebene ist miquelsch.
- Es ist isomorph zur Minkowski-Ebene
mit
(Körper
).
Ein erstaunliches Resultat ist der
Satz(Heise): Jede Minkowski-Ebene gerader Ordnung ist miquelsch.
Bemerkung: Eine geeignete stereographische
Projektion zeigt:
ist isomorph zur Geometrie der ebenen Schnitte auf einem einschaligen
Hyperboloid (Quadrik
vom Index 2) im 3-dimensionalen projektiven Raum über
.
Nicht miquelsche Minkowski-Ebenen
Es gibt zahlreiche nicht miquelsche Minkowski-Ebenen. Aber: Es gibt keine ovoidalen Minkowski-Ebenen (Im
Gegensatz zu Möbius- und Laguerre-Ebenen), weil eine quadratische Menge
vom Index 2 im 3-dimensionalen projektiven Raum schon eine Quadrik ist (s. quadratische
Menge).
Viele nicht miquelsche Beispiele werden durch eine Verallgemeinerung des
Zusammenhangs der Hyperbeln/Geraden mit den gebrochen linearen Abbildungen
(projektive Gruppe )
gewonnen.
Aber auch die blose Ersetzung der Hyperbeln im klassischen Modell durch die
ähnlichen Kurven
liefert nicht miquelsche Minkowski-Ebenen.
Literatur
- W. Benz, Vorlesungen über Geometrie der Algebren, Springer, S. 42–81 (1973)


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.10. 2021