Ebene Kreisgeometrien

Ebene Kreisgeometrien oder Benz-Ebenen ist ein Sammelbegriff für die drei hier beschriebenen Geometrien: Möbius-Ebene, Laguerre-Ebene und Minkowski-Ebene. Grundlegende Arbeiten stammen von dem deutschen Mathematiker Walter Benz.

Möbius-Ebene

→ Hauptartikel: Möbius-Ebene

Klassische Möbius-Ebene: 2d/3d-Modell

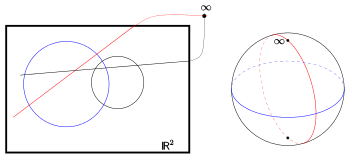
Wir gehen von der reellen euklidischen Ebene aus und fassen die Menge der Geraden und die Menge der Kreise zu einer Blockmenge zusammen. Diese Konstruktion liefert eine sehr inhomogene Inzidenzstruktur. Denn durch je zwei Punkte gehen genau eine Gerade und beliebig viele Kreise. Der Trick, mit dem man diese Inzidenzstruktur in eine homogene Geometrie einbettet, ist die folgende Idee: Man füge der Punktmenge einen weiteren Punkt $\infty$ hinzu, der mit jeder Gerade inzidieren soll. Jetzt ist ein Block durch genau drei Punkte eindeutig bestimmt. Diese "homogenisierte" Geometrie nennt man klassische Möbius-Ebene (nach August Ferdinand Möbius). Die noch bestehende Inhomogenität der Beschreibung (Geraden, Kreise) lässt sich durch ein räumliches Modell beseitigen. Denn mittels einer stereografischen Projektion zeigt man, dass die klassische Möbius-Ebene zur Geometrie der ebenen Schnitte (Kreise) einer Kugel (im 3-dimensionalen Raum) isomorph ist. Analog zu den axiomatischen projektiven Ebenen nennt man eine Inzidenzstruktur, die im Wesentlichen dasselbe Inzidenzverhalten hat wie die klassische Möbius-Ebene, (axiomatische) Möbius-Ebene. Wie zu erwarten, gibt es sehr viele Möbius-Ebenen, die von dem klassischen Modell verschieden sind.

Laguerre-Ebene

→ Hauptartikel: Laguerre-Ebene

Klassische Laguerre-Ebene: 2d/3d-Modell

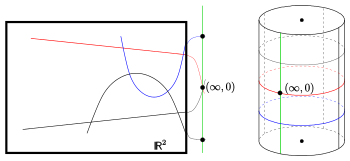
Geht man wieder von $\textstyle \mathbb {R} ^{2}$ aus und nimmt zunächst die Kurven der Form y=ax^2+bx+c (Parabeln und Geraden) als Blöcke, so erweist sich folgende Homogenisierung als nützlich: Man nimmt zur Kurve den neuen Punkt $(\infty ,a)$ hinzu, d.h. die Punktmenge besteht jetzt aus $(\mathbb {R} \cup {\infty })\times \mathbb {R}$ . Diese Geometrie der Parabeln nennt man klassische Laguerre-Ebene (nach Edmond Laguerre). (Sie wurde ursprünglich als die Geometrie der gerichteten Geraden und Kreise formuliert. Beide Geometrien sind zueinander isomorph.) Wie bei der klassischen Möbius-Ebene gibt es auch hier ein räumliches Modell: Die klassische Laguerre-Ebene ist zur Geometrie der ebenen Schnitte auf einem senkrechten Kreiszylinder (im $\mathbb {R} ^{3}$ ) isomorph. Eine Abstraktion wie bei der Möbius-Ebene führt zur (axiomatischen) Laguerre-Ebene.

Minkowski-Ebene

→ Hauptartikel: Minkowski-Ebene

Klassische Minkowski-Ebene: 2d/3d-Modell

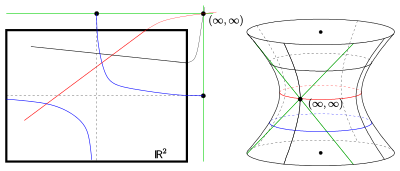
Geht man schließlich von $\mathbb {R} ^{2}$ aus und nimmt zu den Geraden $y=mx+d,m\neq 0$ noch die Hyperbeln $y={\tfrac {a}{x-b}}+c,a\neq 0$ als Blöcke hinzu, so führt die folgende Idee zu einer homogenen Inzidenzstruktur: Man füge jeder Gerade den Punkt $(\infty ,\infty )$ und zu jeder Hyperbel $y={\tfrac {a}{x-b}}+c,a\neq 0$ die Punkte $(b,\infty ),(\infty ,c)$ hinzu, d.h. die Punktmenge besteht in diesem Fall aus $(\mathbb {R} \cup {\infty })^{2}$ . Diese Geometrie der Hyperbeln nennt man die klassische Minkowski-Ebene (nach Hermann Minkowski). Wie bei den klassischen Möbius- und Laguerre-Ebenen gibt es auch hier ein räumliches Modell: Die klassische Minkowski-Ebene ist zur Geometrie der Ebenenschnitte auf einem einschaligen Hyperboloid (nicht ausgeartete Quadrik vom Index 2) im 3-dimensionalen reellen projektiven Raum isomorph. Wie bei Möbius- und Laguerre-Ebene gelangt man durch Abstraktion zur (axiomatischen) Minkowski-Ebene.

Ebene Kreisgeometrien

Da die Blöcke in jedem der drei Fälle projektiv Kreise (nicht ausgeartete Kegelschnitte) sind, benutzt man die Sammelbezeichnung ebene Kreisgeometrien. Das Wort eben soll andeuten, dass es auch höherdimensionale Möbius-, Laguerre- und Minkowski-Geometrien gibt. In der englischen Literatur werden die ebenen Kreisgeometrien auch Benz-Ebenen (Benz planes) nach dem deutschen Mathematiker Walter Benz genannt.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de