Satz von Miquel

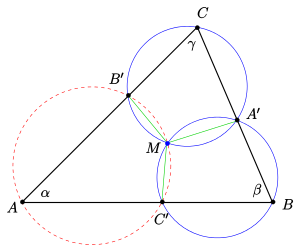
Satz von Miquel: Dreieck und 3 Kreise

Der Satz von Miquel, benannt nach Auguste Miquel, macht eine Aussage über Schnittpunkte von drei Kreisen durch jeweils eine Ecke eines Dreiecks in der reellen Ebene (s. Bild):

Es sei ein Dreieck mit den Eckpunkten , den Seiten $BC,AC,AB$ und drei Punkten $A^{\prime }$ auf $BC,B^{\prime }$ auf und $C^{\prime }$ auf . Dann gilt: Die 3 Kreise durch $AB^{\prime }C^{\prime },A^{\prime }BC^{\prime }$ , und $A^{\prime }B^{\prime }C$ schneiden sich in einem Punkt .

Der Beweis ergibt sich durch 3-malige Anwendung des Satzes über ein Kreisviereck: Vier Punkte liegen nur dann auf einem Kreis, wenn sich im Viereck gegenüber liegende Winkel zu 180 Grad ergänzen. Es sei der Schnittpunkt der beiden Kreise $A^{\prime }BC^{\prime }$ und $A^{\prime }B^{\prime }C$ und $\alpha,\beta,\gamma$ seien die Winkel im Dreieck A,B,C . Dann ist der Winkel bei im Kreisviereck $A^{\prime }MBC^{\prime }$ $180^{\circ }-\beta$ und der Winkel bei im Kreisviereck $A^{\prime }MB^{\prime }C$ ist $180^{\circ }-\gamma$ . Also ist der Winkel im Viereck $AB^{\prime }MC^{\prime }$ bei gleich $360^{\circ }-(180^{\circ }-\beta +180^{\circ }-\gamma )=\beta +\gamma =180^{\circ }-\alpha$ , d.h. die vier Punkte $A,B^{\prime },M,C^{\prime }$ liegen auf einem Kreis.

Satz von Miquel: 6-Kreise-Form

Beschreibt man die reelle Ebene in üblicher Weise mit den komplexen Zahlen $\mathbb {C}$ (s. Gauß'sche Zahlenebene) und ergänzt die komplexen Zahlen um das Symbol $\infty$ , das auf allen Geraden liegen soll, so erhält man ein Modell der klassischen Geometrie der Kreise, die auch Möbius-Ebene genannt wird. Die gebrochen linearen Abbildungen $PGL(2,\mathbb {C} )$ , die Möbiustransformationen, bilden Kreise und komplettierte Geraden auf ebensolche ab. Bildet man die obige Miquel-Figur mit einer geeigneten Möbiustransformation so ab, dass die Seiten des Dreiecks auf richtige Kreise übergehen, erhält man den Satz von Miquel in allgemeiner Form:

Kann man 8 Punkte $P_{1},...,P_{8}$ so den Ecken eines Würfels zuordnen, dass die jeweils einer Seitenfläche zugeordneten Punkte 5-mal auf einem Kreis liegen, so ist dies auch für das 6. Viereck der Fall (s. Bild).

Bedeutung des Satzes von Miquel:

Der Satz von Miquel spielt eine wichtige Rolle bei der Klassifizierung axiomatischer Möbius-Ebenen.
Den Satz von Miquel gibt es auch für Parabeln und Hyperbeln und spielt bei der Klassifizierung der Laguerre-Ebenen und Minkowski-Ebenen eine wichtige Rolle.

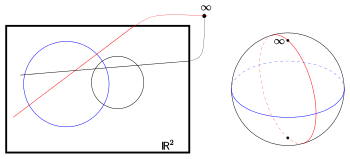
klassische Möbius-Ebene:2d/3d-Modell

Bemerkung: Mit Hilfe einer stereografischen Projektion überzeugt man sich, dass die klassische Möbiusebene zur Geometrie der Kreise auf der Einheitskugel isomorph ist. Hier gibt es nur Kreise (keine Geraden) und die allgemeine Form des Satzes von Miquel ist eine Aussage über 6 Kreise im $\mathbb {R} ^{3}$ .

Literatur

M. Koecher, A. Krieg: Ebene Geometrie. 3. Auflage. Springer-Verlag, 2007, ISBN 978-3-540-49327-3.

Basierend auf einem Artikel in:

Wikipedia.de