Projektives Koordinatensystem
Ein projektives Koordinatensystem erlaubt es, die Lage eines Punktes in einem projektiven Raum eindeutig durch die Angabe eines Koordinatenvektors zu beschreiben. Dadurch können in den mathematischen Gebieten der Geometrie und der linearen Algebra die strukturerhaltenden Abbildungen von projektiven Räumen (das sind die Kollineationen und vor allem die projektiven Abbildungen) durch koordinatenbezogene Abbildungsmatrizen dargestellt und die Räume mit Methoden der analytischen Geometrie untersucht werden.
Die Komponenten des Koordinatenvektors, der einen Punkt im projektiven Raum beschreibt, heißen projektive Koordinaten. Sie werden auch als homogene Koordinaten bezeichnet. (→ im Hauptartikel „Homogene Koordinaten“ wird auch erläutert, wie projektive Koordinaten zur Kennzeichnung von Elementen verwandter Strukturen wie affiner Räume verwendet werden können.)
In einem abstrakten projektiven Raum endlicher Dimension
ist das Koordinatensystem durch
geeignet gewählte Basispunkte bestimmt – die Punkte müssen in allgemeiner Lage
gewählt sein und werden dann als projektive
Basis bezeichnet. Der Bezug auf Basispunkte an Stelle einer Vektorraumbasis
(Hamelbasis), die im Standardmodell völlig ausreicht, ermöglicht eine
modellunabhängige geometrische Beschreibung des Bezugssystems und in der synthetischen
Geometrie die Einführung vergleichbarer Koordinaten auch in allgemeineren
Strukturen (insbesondere projektiven
Inzidenzebenen), denen kein Vektorraum
und damit kein Körper
als Koordinatenbereich zugeordnet werden kann.
Projektive Koordinaten im Standardmodell
Es sei
der
-dimensionale
projektive
Raum über dem Körper
.
Die projektiven Punkte, die zu einer Vektorraumbasis
des
gehören, also die von diesen Basisvektoren erzeugten eindimensionalen
Unterräume
bilden zusammen mit dem Einheitspunkt
eine projektive
Basis (auch: projektive Punktbasis)
des projektiven Raumes
.
Durch Schlitzen entlang der durch
verlaufenden projektiven Hyperebene erhält man einen affinen Raum
.
In diesem sei
der Nullpunkt. Wir betrachten für
den Schnittpunkt
der Geraden
mit der Hyperebene durch
.
Diese Punkte
bilden mit dem Nullpunkt
eine affine Basis von
.
Mit dieser Basis können wir affine Koordinaten
in
definieren und die projektiven Koordinaten bezüglich der gewählten projektiven
Basis sind dann per Definition
.
Beispiel
Es wird der Raum
mit der Standardbasis
betrachtet. Dann haben die projektiven Geraden
und
den Schnittpunkt
und die projektiven Geraden
und
den Schnittpunkt .
Die projektiven Koordinaten des Punktes
sind dann
für
.
Projektive Koordinaten in der synthetischen Geometrie
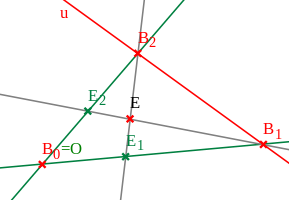
In einer beliebigen, auch nichtdesargueschen projektiven Ebene können projektive Koordinaten nach Wahl einer projektiven Basis mit Hilfe affiner Koordinaten eingeführt werden.
In der projektiven Ebene muss zunächst eine rojektive
Basis
gewählt worden sein, das heißt, keine drei der vier Punkte sollen auf einer
gemeinsamen Geraden liegen. Der Punkt
wird zum Ursprung
des affinen Koordinatensystems, die Verbindungsgerade
zu seiner ersten,
zu seiner zweiten Koordinatenachse. Die zunächst noch projektiven Schnittpunkte
und
sind die Einheitspunkte auf diesen Achsen, somit ist
eine affine Punktbasis der affinen Ebene, die aus der projektiven durch
Schlitzen längs der Gerade
entsteht. Diese Gerade wird zur Ferngerade
der affinen Ebene, siehe dazu auch die Abbildung rechts.
- Für jeden Punkt der geschlitzten Ebene können durch Koordinatenkonstruktion affine Koordinaten
bestimmt werden, wobei der Koordinatenbereich
durch die erste Achse des affinen Koordinatensystems repräsentiert wird. → Die Koordinatenkonstruktion ist im Artikel Ternärkörper beschrieben.
- Ein Punkt außerhalb von
mit den affinen Koordinaten
erhält die projektiven Koordinaten
.
- Ein Punkt
auf der Ferngeraden
erhält die projektiven Koordinaten
, wobei
die affinen Koordinaten des Punktes
auf der Verbindungsgerade
sind. (Aus der vorausgesetzten "allgemeinen Lage" folgt
und mithin
.)
Die so bestimmten Koordinaten sind für Punkte außerhalb von
eindeutig, für Punkte auf
kann diese Eindeutigkeit durch zusätzliche Vereinbarungen erreicht werden. Sie
sind im Allgemeinen nicht homogen: Im Koordinatenbereich
,
der ein Ternärkörper ist, lässt sich im Allgemeinen keine „Skalarmultiplikation“
definieren.
Anwendungen
Abbildungen
Wenn
und
projektive Räume der Dimension
bzw.
über einem festen Körper
sind, dann gilt:
- Jede projektive
Abbildung
von
nach
besitzt bezüglich fest gewählter projektiver Punktbasen in
und
eine Darstellung
. Die Abbildungsmatrix
hat
Zeilen und
Spalten und ist bis auf einen skalaren Faktor
eindeutig bestimmt.
- Wählt man zu jedem Punkt
einer projektiven Punktbasis von
oder gleichwertig zu
Punkten in allgemeiner Lage, jeweils einen beliebigen Bildpunkt
, dann lässt sich dies eindeutig zu einer projektiven Abbildung
fortsetzen, bei der also
für jeden Basispunkt gilt.
- Jede Projektivität
auf
besitzt bezüglich einer fest gewählten projektiven Punktbasis in
eine Darstellung
. Die quadratische, reguläre
Abbildungsmatrix
ist bis auf einen skalaren Faktor
eindeutig bestimmt.
- Zu
Urbildpunkten
in allgemeiner Lage und
Bildpunkten
in allgemeiner Lage gibt es genau eine Projektivität
auf
, bei der
ist. Man sagt daher auch, die projektive lineare Gruppe
operiert scharf einfach transitiv auf der Menge der
-Tupel von Punkten in allgemeiner Lage.
- Ist die Dimension
, dann lässt sich jede Kollineation
auf
bezüglich einer fest gewählten projektiven Basis in
als Komposition
mit einer Projektivität
und einem Automorphismus
des Körpers
darstellen.
Doppelverhältnis
Das Doppelverhältnis
von vier kollinearen Punkten
in einem projektiven Raum ist das einfache Verhältnis der projektiven
Koordinaten, die der Punkt
hat, wenn die übrigen drei Punkte als Punktbasis der gemeinsamen Geraden gewählt
werden. Dabei sind
die Basispunkte und
der Einheitspunkt des Koordinatensystems. Hat nun
bezüglich dieses Systems die Koordinatendarstellung
,
dann gilt für das Doppelverhältnis:
.
Dieser Zusammenhang ist einer der Gründe dafür, dass das Doppelverhältnis
auch gelegentlich als inhomogene projektive Koordinate von
(bezüglich der anderen Punkte im Doppelverhältnis) bezeichnet wird.
Parametergleichungen
- Die Verbindungsgerade von zwei verschiedenen Punkten
und
hat die homogene Parameterdarstellung
Dabei sind dann
für
die projektiven Koordinaten eines Geradenpunktes
- Allgemeiner ist der Verbindungsraum von
Punkten
, deren Koordinatenvektoren linear unabhängig sind, ein
-dimensionaler Unterraum des projektiven Raumes mit der Parameterdarstellung
Koordinatengleichungen und Hyperebenenkoordinaten
Nach der Wahl einer projektiven Punktbasis
in einem
-dimensionalen
projektiven Raum
kann man jedem Punkt
eindeutig die Koordinatengleichung
zuordnen, deren Lösungsmenge, als Punktkoordinaten aufgefasst, einen
-dimensionalen
Unterraum von
,
also eine Hyperebene beschreibt. Da
die Gleichung homogen ist, ändert sich ihre Lösungsmenge nicht, wenn man jede
Koordinate mit dem gleichen Skalar
multipliziert, die Hyperebene hängt also nur vom Punkt
und dem gewählten projektiven Koordinatensystem ab. Man bezeichnet den
Koordinatenvektor
als Hyperebenenkoordinaten dieser Hyperebene. Jedem Punkt des Raumes wird
so durch Dualisierung
eineindeutig eine Hyperebene zugeordnet.
Dualität in projektiven Räumen
Die duale Zuordnung von Punkten zu Hyperebenen kann zu einer Dualität im Verband der projektiven Teilräume eines Projektiven Raumes ausgebaut werden. Dabei gelten folgende Zuordnungen:
| Begriff | Dualer Begriff |
|---|---|
| Punkt | Hyperebene |
| Gesamtraum | Leere
Menge als |
| Schnitt |
Verbindungsraum |
| Doppelverhältnis von vier kollinearen Punkten | Doppelverhältnis von vier Hyperebenen, die sich in einem |
Die Zuordnung ist auch umgekehrt zu verstehen, da die Dualisierung involutorisch ist: Einer Hyperebene entspricht dual ein Punkt. Während die konkrete Dualisierung vom gewählten Koordinatensystem abhängt, sind allgemeine Sätze davon nicht betroffen.
Das Dualitätsprinzip der projektiven Geometrie beruht auf dem
algebraischen Dualraum des endlichdimensionalen Koordinatenvektorraums
,
siehe dazu den Hauptartikel „Dualraum“.
Anwendungsbeispiele in der ebenen Geometrie finden sich in „Dualität
(Mathematik)“ im Abschnitt „Dualitätsprinzip
der projektiven Geometrie und in Inzidenzstrukturen“.
Dreidimensionale Beispiele
In einem dreidimensionalen Raum
ist die Menge der Geraden (eine Gerade entspricht einem 2-dimensionalen
Unterraum von
)
zu sich selbst dual. Die konkrete Gerade
ist dual zu
Dies ist eine zu
windschiefe Gerade! Die Aussage „Die Geraden
und
schneiden einander nicht.“ ist dual zu „Der Verbindungsraum von
und
ist der gesamte dreidimensionale Raum.“ Für zwei beliebige windschiefe Geraden
und
kann stets eine Punktbasis gewählt werden, bezüglich der
gilt – man wählt zu jeder Geraden zwei linear unabhängige, erzeugende Vektoren
und ergänzt diese vier Vektoren durch ihre Summe als Einheitspunkt. Also sind
die Aussagen „Zwei Geraden schneiden einander nicht“ und „Zwei Geraden spannen
den Raum auf“ zueinander duale Beschreibungen der Eigenschaft „windschief“.
Dagegen sind die Aussagen „
und
schneiden sich in einem Punkt“ und „
und
spannen eine Ebene auf“ äquivalent aber nicht dual zueinander, da die erste
Aussage nicht für beliebige Paare von Geraden gilt und die dazu duale Aussage
von anderen Geraden handelt!


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.02. 2020