Projektive Basis
Eine projektive Basis ist in der Mathematik
eine Menge von
Punkten eines
-dimensionalen
projektiven
Raums, von denen je
projektiv unabhängig sind. Projektive Basen werden in der projektiven
Geometrie zur Charakterisierung von Projektivitäten
und zur Definition projektiver
Koordinaten verwendet.
Definition
Ein -Tupel
von Punkten eines projektiven
Raums
über einem
-Vektorraum
heißt projektiv unabhängig, wenn eine der folgenden äquivalenten
Bedingungen zutrifft:
- Es gibt linear
unabhängige Vektoren
mit
für
.
- Jedes
-Tupel
von Vektoren aus
mit
für
ist linear unabhängig.
- Für die Dimension
des Verbindungsraums
der Punkte gilt
.
Ein -Tupel
von Punkten eines projektiven Raums heißt projektive Basis des Raums,
wenn je
Punkte projektiv unabhängig sind. Es gilt dann
.
Spezialfälle
: drei Punkte auf einer projektiven Geraden bilden genau dann eine projektive Basis, wenn sie paarweise verschieden sind.
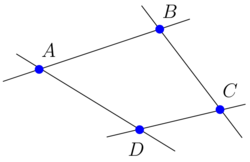
: vier Punkte auf einer projektiven Ebene bilden genau dann eine projektive Basis, wenn keine drei davon auf einer Geraden liegen. Die vier Punkte bestimmen also ein vollständiges Viereck.
: fünf Punkte in einem dreidimensionalen projektiven Raum bilden genau dann eine projektive Basis, wenn keine vier davon in einer Ebene liegen.
Projektive Standardbasis
Die projektive Standardbasis
im projektiven Standardraum
besteht aus den von den Standard-Basisvektoren
des Koordinatenraums
erzeugten Punkten
,
zusammen mit dem Einheitspunkt
.
In homogenen Koordinaten ergeben sich beispielsweise folgende projektiven Standardbasen:
- In der projektiven Gerade
über einem Körper
bilden die
Punkte
und
die projektive Standardbasis.
- In der projektiven Ebene
über einem Körper
bilden die
Punkte
und
die projektive Standardbasis.
- Im
-dimensionalen projektiven Raum
über einem Körper
bilden die
Punkte
und
die projektive Standardbasis.
Verwendung
Ist
eine beliebige projektive Basis eines projektiven Raums
,
dann gibt es eine Basis
von
,
sodass
gilt.
Sind nun
und
zwei projektive Räume gleicher Dimension mit projektiven Basen
und
,
dann gibt es genau eine projektive
Abbildung
,
sodass
für
gilt.
Demnach ist eine projektive Abbildung zwischen projektiven Räumen gleicher
Dimension durch Angabe der Bilder der projektiven Basispunkte eindeutig
charakterisiert. Solche Abbildungen lassen sich daher durch Matrizen der Größe
beschreiben. Weiter lassen sich in einem projektiven Raum
mit der projektiven Basis
mit Hilfe der projektiven Abbildung
homogene projektive Koordinaten definieren.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.03. 2017