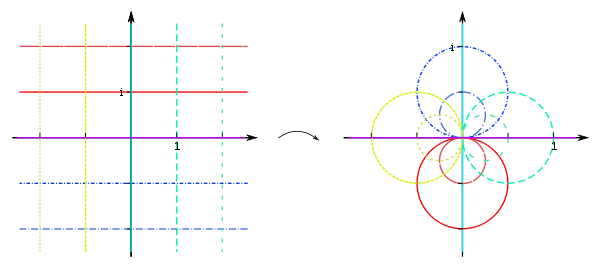Projektive Gerade
In der Mathematik, insbesondere der projektiven Geometrie ist die projektive Gerade ein eindimensionaler projektiver Raum.
Definition
Es sei
ein Körper,
zum Beispiel der Körper der reellen
oder komplexen Zahlen oder ein
endlicher
Körper. Es sei
der (bis auf Isomorphie
eindeutige) zweidimensionale
-Vektorraum. Die
projektive Gerade
ist die Menge der eindimensionalen Untervektorräume
von
.
Mit anderen Worten: die projektive Gerade ist der Quotientenraum
bezüglich der Äquivalenzrelation
.
Diese Äquivalenzrelation identifiziert zwei Punkte genau dann, wenn sie im selben eindimensionalen Untervektorraum, also auf derselben Gerade durch den Nullpunkt liegen.
Homogene Koordinaten
Jeder Punkt der projektiven Gerade kann in homogenen Koordinaten als
mit
dargestellt werden, wobei
für alle
gilt.
Zahlengerade erweitert um den Punkt im Unendlichen
Die projektive Gerade
kann mit
,
der um einen "Punkt
im Unendlichen" erweiterten Gerade
identifiziert werden. Man kann nämlich die Gerade
mit der in homogenen Koordinaten durch
gegebenen Teilmenge der
identifizieren. Diese Teilmenge enthält dann alle Punkte der
bis auf einen, den sogenannten "Punkt im Unendlichen":
Beispiele
- Die reelle projektive Gerade
ist homöomorph zum Kreis
.
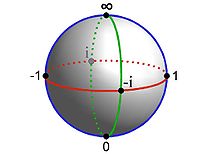
- Die komplexe projektive Gerade
wird als Riemannsche Zahlenkugel bezeichnet, sie ist homöomorph zur 2-Sphäre
.
- Die projektive Gerade
über dem endlichen Körper
hat
Elemente.
Automorphismen
Die allgemeine
lineare Gruppe
wirkt auf
durch lineare
Abbildungen. Die projektive
lineare Gruppe
ist die Faktorgruppe
,
wobei
die normale (sogar zentrale)
Untergruppe der skalaren Vielfachen
der Identität
ist mit
aus
.
Die Wirkung von
auf
induziert eine wohldefinierte
Wirkung von
auf
.
Die Automorphismen von
sind per Definition die durch Elemente von
beschriebenen Abbildungen
.
In homogenen Koordinaten wirken die Matrizen als gebrochen-lineare Transformationen:
nach der Identifizierung .
Die Automorphismengruppe wirkt transitiv auf Tripeln paarweise unterschiedlicher Punkte.
Eine fundamentale Invariante der projektiven Geometrie ist das Doppelverhältnis von 4-Tupeln paarweise unterschiedlicher Punkte. Falls K algebraisch abgeschlossen ist, lassen sich zwei solche 4-Tupel genau dann durch einen Automorphismus ineinander überführen, wenn ihr Doppelverhältnis übereinstimmt.
Im Fall
bezeichnet man die Automorphismen von
als Möbiustransformationen.
Projektive Geraden in der projektiven Ebene
Die projektive Gerade durch zwei gegebene Punkte
und
der projektiven Ebene bestimmt man, indem man die beiden Punkte als Geraden im
auffaßt (und durch ihre Geradengleichung
beschreibt), die sie enthaltende Ebene im
berechnet (siehe Ebenengleichung)
und diese Ebene dann auf eine projektive Gerade in
projiziert.
Analog bestimmt man projektive Geraden durch zwei gegebene Punkte in einem höherdimensionalen projektiven Raum.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.02. 2020