
Moufang-Ebene
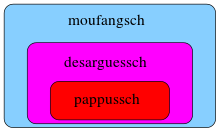
desarguessch: der große Satz von Desargues,
pappussch: der Satz von Pappus
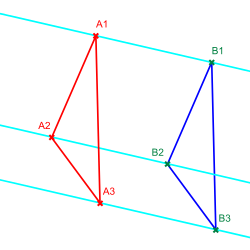
Moufang-Ebenen sind projektive Ebenen, in denen der kleine projektive Satz von Desargues allgemeingültig ist. Sie sind nach der deutschen Mathematikerin Ruth Moufang benannt, die diese Ebenen in den 1930er Jahren untersuchte. Sie konnte zeigen, dass jede Moufang-Ebene isomorph zu einer projektiven Ebene über einem Alternativkörper ist. Da ein endlicher Alternativkörper schon ein Körper ist (s.u.), gilt: Alle endlichen Moufang-Ebenen sind pappussche Ebenen. (Man beachte: In einer desargueschen projektiven Ebene gilt der große Satz von Desargues. Eine solche Ebene ist über einem Schiefkörper koordinatisierbar und jeder Schiefkörper ist ein Alternativkörper, aber nicht umgekehrt.)
Moufang-Ebenen bilden die Klasse VII in der Klassifikation der projektiven Ebenen nach Hanfried Lenz.
Ist
ein Alternativkörper, dann kann
zu einer projektiven Ebene gemacht werden, indem man wie bei einem projektiven
Raum über einem Körper die von einem Element
erzeugten eindimensionalen Unterräume
als Punkte und die zweidimensionalen Unterräume als Geraden
verwendet. Man spricht dann auch von der projektiven Ebene über
und notiert sie als
.
Diese projektiven Koordinatenebenen sind stets Moufang-Ebenen. Genau dann, wenn
die Multiplikation im Alternativkörper
das Assoziativgesetz
erfüllt, ist
ein Schiefkörper
und die Ebene
eine desarguessche projektive Ebene. Man beachte aber, dass zu einem
Alternativkörper
,
der kein Schiefkörper ist, keiner der formal darstellbaren
Koordinatenräume
für
eine projektive
Geometrie bildet, vergleiche dazu Axiom
von Veblen-Young!
Jede Moufang-Ebene ist isomorph zu einer projektiven Koordinatenebene
über einem Alternativkörper
,
der durch die Ebene bis auf Isomorphie eindeutig bestimmt ist.
Mit einem Satz von Artin
und Zorn, der besagt, dass jeder endliche Alternativkörper ein Körper ist,
folgt daraus, dass jede endliche Moufang-Ebene tatsächlich eine projektive Ebene
über einem endlichen
Körper ist.
Äquivalente Beschreibungen für den Begriff „Moufang-Ebene“: Eine projektive Ebene ist genau dann eine Moufang-Ebene, wenn
- jede durch Schlitzen (affine Beschränkung bezügl. einer Gerade als Ferngerade) aus ihr entstehende affine Ebene eine affine Translationsebene ist,
- alle Ternärkörper, die man der Ebene als Koordinatenbereich durch Wahl eines projektiven Koordinatensystems, also durch Wahl eines vollständigen Vierecks als Punktbasis zuordnen kann, isomorph sind,
- einer der Koordinatenternärkörper ein Alternativkörper ist,
- für jede Gerade der Ebene die Gruppe der Kollineationen, die die Gerade punktweise festlassen, transitiv auf der Menge der Punkte, die nicht auf der Geraden liegen, operiert,
- die Gruppe der Kollineationen transitiv auf der Menge der vollständigen Vierecke (aufgefasst als geordnete Menge der vier Ecken) operiert.
Bei einer Moufang-Ebene sind die genannten affinen Translationsebenen alle zueinander isomorph (als Inzidenzstrukturen), ihre Koordinatenternärkörper sind stets Quasikörper und sogar Alternativkörper, die ebenfalls zueinander isomorph sind.
Die reellen Oktonionen
sind ein Beispiel für einen Alternativkörper, der kein Schiefkörper ist, die
projektive Ebene
das wichtigste Beispiel für eine nichtdesarguesche Moufang-Ebene.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.10. 2019