Seitenhalbierende

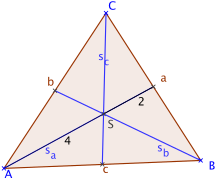
Die Seitenhalbierenden im Dreieck.
S, der Schnittpunkt der drei Seitenhalbierenden, ist der Schwerpunkt des Dreiecks. Er teilt die Seitenhalbierenden jeweils im Verhältnis 2:1.

Eine Seitenhalbierende (auch Schwerlinie oder Median) in einem Dreieck ist eine Strecke, die eine Ecke des Dreiecks mit dem Mittelpunkt der gegenüberliegenden Seite verbindet. Die Seitenhalbierenden gehören zusammen mit den Mittelsenkrechten (Streckensymmetralen), Winkelhalbierenden (Winkelsymmetralen) und den Höhen zu den klassischen Transversalen der Dreiecksgeometrie.

Eigenschaften

Die Seitenhalbierende teilt die Dreiecksfläche in zwei Dreiecke gleicher Höhe bzgl. der gemeinsamen Grundseite und damit auch gleicher Fläche. Mittels Scherung parallel zur Seitenhalbierenden lassen sich die beiden Teildreiecke unter Beibehaltung ihres Flächeninhalts in eine achsensymmetrische Form überführen. Diese Scherung lässt die Verteilung der Flächenelemente innerhalb der Teildreiecke und damit das Drehmoment der einzelnen Dreiecksflächen bezogen auf die gemeinsame Grundseite unverändert. Die drei Seitenhalbierenden eines Dreiecks sind somit Schwerlinien und schneiden sich in einem Punkt, dem so genannten Schwerpunkt des Dreiecks. Dieser teilt jede der Seitenhalbierenden im Verhältnis 2:1. Dabei ist die Strecke zwischen Schwerpunkt und Ecke länger als die Strecke zwischen Schwerpunkt und Seitenmittelpunkt.

Die Längen der zur Seite a, b und c gehörenden Seitenhalbierenden berechnet man mit:

$s_a = \frac{\sqrt{2(b^2+c^2)-a^2}}{2}$

$s_b = \frac{\sqrt{2(c^2+a^2)-b^2}}{2}$

$s_c = \frac{\sqrt{2(a^2+b^2)-c^2}}{2}$

Mediane in Tetraedern

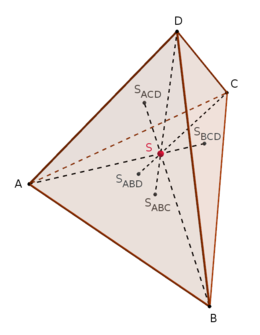
Mediane eines Tetraeders mit Schwerpunkt S

${\begin{aligned}&{\frac {|AS|}{|SS_{BCD}|}}={\frac {|BS|}{|SS_{ACD}|}}={\frac {|CS|}{|SS_{ABD}|}}\\=&{\frac {|DS|}{|SS_{BBC}|}}={\frac {3}{1}}\end{aligned}}$

In einem Tetraeder bezeichnet man eine Strecke, die einen Eckpunkt mit dem Schwerpunkt der dem Eckpunkt gegenüberliegenden Dreiecksfläche verbindet, als Median des Tetraeders. Die vier Mediane einen Tetraeders schneiden sich in einem Punkt, dem Schwerpunkt des Tetraeders. Dieser teilt die Mediane in einem Verhältnis von 3:1 (Satz von Commandino).

Literatur

Claudi Alsina, Roger B. Nelsen: Perlen der Mathematik: 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen. Springer, 2015, ISBN 978-3-662-45461-9.
Harald Scheid, Wolfgang Schwarz: Elemente der Geometrie. 5. Auflage. Springer, 2016, ISBN 978-3-662-50323-2.

Basierend auf einem Artikel in:

Wikipedia.de