Orthoptische Kurve

Die orthoptische Kurve (griechisch ορθοπτική ‚Geradesehen‘) einer ebenen Kurve ist in der Mathematik der geometrische Ort aller Schnittpunkte orthogonaler Tangenten der Kurve .

Parabel mit orthoptischer Kurve (lila Gerade).

Ellipse mit orthoptischer Kurve (lila Kreis)

Hyperbel mit orthoptischer Kurve (lila Kreis)

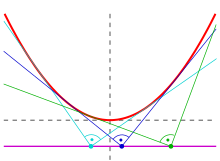
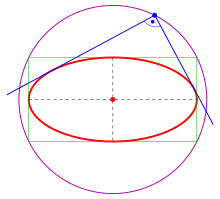
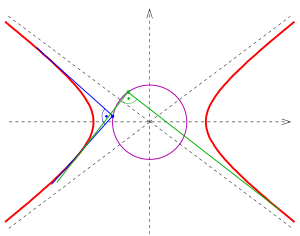
Beispiele: Die orthoptische Kurve

einer Parabel ist ihre Leitlinie (Beweis: siehe unten),
einer Ellipse ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ ist der Kreis $x^{2}+y^{2}=a^{2}+b^{2}$ (s. unten),
einer Hyperbel ${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1,\,a>b,$ ist der Kreis $x^{2}+y^{2}=a^{2}-b^{2}$ (im Fall $a\leq b$ gibt es keine orthogonalen Tangenten, s. unten),
einer Astroide $x^{2/3}+y^{2/3}=1$ ist die 4-blättrige Rosette (Quadrifolium) mit der Gleichung (in Polarkoordinaten)

$r=\tfrac{1}{\sqrt{2}}\cos(2\varphi), \ 0\le \varphi <2\pi,$ (siehe unten).

Verallgemeinerungen:

Eine isoptische Kurve einer ebenen Kurve ist der geometrische Ort aller Schnittpunkte von Tangenten der Kurve die sich unter einem festen Winkel schneiden (s. unten).
Eine isoptische Kurve zweier ebener Kurven $k_{1},k_{2}$ ist der geometrische Ort aller Schnittpunkte von Tangenten der Kurven $k_{1},k_{2}$ , die sich unter einem festen Winkel schneiden.
Der Thaleskreis über einer Strecke $\overline {P_{1}P_{2}}$ lässt sich als orthoptische Kurve von zwei zu den Punkten $P_{1},P_{2}$ degenerierten Kreisen auffassen.

Bemerkung: In der Augenheilkunde gibt es die ähnlich lautenden Begriffe Orthoptik und Orthoptistin.

Orthoptische Kurve einer Parabel

Eine beliebige Parabel lässt sich durch eine geeignete Verschiebung und Drehung in einem kartesischen Koordinatensystem durch eine Gleichung y=ax^2 beschreiben. Die Steigung in einem Parabelpunkt $(x,ax^{2})$ ist m=2ax . Ersetzt man in $(x,ax^{2})$ die Variable durch $x={\tfrac {m}{2a}}$ , so erhält man eine Parameterdarstellung der Parabel mit der Steigung als Parameter: $\ ({\tfrac {m}{2a}},{\tfrac {m^{2}}{4a}})\;.$ Die Tangente in einem Parabelpunkt hat die Gleichung $y=mx+n$ mit dem noch unbekannten -Abschnitt , der durch Einsetzen der Koordinaten des Parabelpunktes bestimmt werden kann. Man erhält $\ y=mx-{\tfrac {m^{2}}{4a}}\;.$ Für einen beliebigen Punkt $(x,y)=(x_{0},y_{0})$ einer solchen Tangente gilt also für die Steigung die quadratische Gleichung

$y_{0}=mx_{0}-{\frac {m^{2}}{4a}}\ \leftrightarrow \ \quad m^{2}-4ax_{0}\;m+4ay_{0}=0\;,$

deren Lösungen $m_{1},m_{2}$ die Steigungen der beiden Tangenten durch $(x_{0},y_{0})$ sind. Das Absolutglied dieser Gleichung ist nach dem Satz von Vieta dem Produkt ihrer Lösungen gleich, das wegen der vorausgesetzten Orthogonalität der Tangenten gleich −1 sein muss:

$m_{1}m_{2}=4ay_{0}=-1$

Die letzte Gleichung ist zu

$y_{0}=-{\frac {1}{4a}}$

äquivalent. Sie ist die Gleichung der Leitlinie der Parabel.

Orthoptische Kurve einer Ellipse bzw. Hyperbel

Ellipse

Sei $\;E:\;{\tfrac {x^{2}}{a^{2}}}+{\tfrac {y^{2}}{b^{2}}}=1\;$ die betrachtete Ellipse.

(1) Die senkrechten Tangenten an durch die Hauptscheitel $(\pm a,0)$ schneiden die waagrechten Tangenten durch die Nebenscheitel $(0,\pm b)$ in den Punkten $(\pm a,\pm b)$ . Diese vier Schnittpunkte liegen auf einem Kreis um den Koordinatenursprung mit Radius $\sqrt{a^2+b^2}$ .

(2) Bis auf die Hauptscheitel ist jeder Punkt (u,v) der Ellipse Berührpunkt einer Tangente mit der Hauptform y=mx+n . Auflösen der Tangentengleichung ${\frac {u}{a^{2}}}x+{\frac {v}{b^{2}}}y=1$ (s. Ellipse) nach ergibt

$m=-{\frac {b^{2}u}{a^{2}v}}$ und $n={\frac {b^{2}}{v}}$ .

Wegen Punktsymmetrie zum Koordinatenursprung existieren zu jeder Steigung zwei parallele Tangenten $t_{1,2}$ , deren Hauptformen sich genau im Vorzeichen von unterscheiden. Für je ein Paar $t_{1,2}$ ist $n^{2}$ nur von abhängig, und die Lage von (u,v) auf der Ellipse ermöglicht eine koordinatenfreie Darstellung:

$n^{2}\cdot 1={\frac {b^{4}}{v^{2}}}\cdot ({\frac {u^{2}}{a^{2}}}+{\frac {v^{2}}{b^{2}}})=(\pm {\frac {b^{2}u}{av}})^{2}+b^{2}=m^{2}a^{2}+b^{2}$

Das ergibt für die allgemeine Hauptform einer nicht senkrechten Tangente an :

$y=m\;x\;\pm {\sqrt {m^{2}a^{2}+b^{2}}}$

Für einen beliebigen Punkt $(x,y)=(x_{0},y_{0})$ einer solchen Tangente ergibt Auflösen der Funktionsgleichung nach die quadratische Gleichung

$m^{2}-{\frac {2x_{0}y_{0}}{x_{0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=0,$

deren Lösungen $m_{1},m_{2}$ die Steigungen der beiden Tangenten durch $(x_{0},y_{0})$ sind. Das Absolutglied dieser Gleichung ist nach dem Satz von Vieta dem Produkt ihrer Lösungen gleich. Bis auf die in (1) betrachteten schneiden sich zwei Tangenten mit dem Steigungsprodukt orthogonaler Geraden in $(x_{0},y_{0})$ genau dann orthogonal, wenn

${\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=m_{1}m_{2}=-1$

oder äquivalent

$x_{0}^{2}+y_{0}^{2}=a^{2}+b^{2}$ .

(3) Mit (1) und (2) gilt allgemein:

Die Schnittpunkte orthogonaler Tangenten liegen auf einem Kreis um den Ursprung mit Radius ${\sqrt {a^{2}+b^{2}}};$ dieser ist die orthoptische Kurve der Ellipse . Äquivalent:
Von einem beliebigen Punkt des orthoptischen Kreises aus erscheint die Ellipse unter einem Öffnungswinkel von $90^{\circ }.$

Hyperbel

Der Ellipsenfall lässt sich für den Hyperbelfall fast wörtlich übernehmen. Die einzigen notwendigen Änderungen sind: 1) man ersetze $b^{2}$ durch $-b^{2}$ und 2) schränke durch |m|>b/a ein. Damit erhält man:

Die Schnittpunkte orthogonaler Tangenten liegen auf einem festen Kreis mit Radius ${\sqrt {a^{2}-b^{2}}}.$ Dabei muss sein.

Orthoptische Kurve einer Astroide

Orthoptische Kurve (lila) einer Astroide

Eine Astroide lässt sich durch die Parameterdarstellung

${\vec c}(t)=(\cos ^{3}t,\sin ^{3}t),\;0\leq t<2\pi$

beschreiben. Mit Hilfe der Bedingung ${\vec {\dot c}}(t)\cdot {\vec {\dot c}}(t+\alpha )=0$ stellt man fest, in welchem Abstand $\alpha$ (im Parameterbereich) sich eine zu ${\vec {\dot c}}(t)$ orthogonale Tangente befindet. Unabhängig vom Parameter ergibt sich, dass $\alpha =\pm {\tfrac {\pi }{2}}$ gilt. Die Gleichungen der (orthogonalen) Tangenten in den Punkten $\vec c(t)$ und ${\vec c}(t+{\tfrac {\pi }{2}})$ sind:

$y=-\tan t(x-\cos ^{3}t)+\sin ^{3}t$

$y={\tfrac {1}{\tan t}}(x+\sin ^{3}t)+\cos ^{3}t$

Ihr Schnittpunkt hat die Koordinaten:

$x=\sin t\cos t(\sin t-\cos t)$

$y=\sin t\cos t(\sin t+\cos t)$

Dies ist zugleich eine Parameterdarstellung der zugehörigen orthoptischen Kurve. Eliminiert man den Parameter so ergibt sich die implizite Darstellung

$2(x^{2}+y^{2})^{3}-(x^{2}-y^{2})^{2}=0.$

Führt man den neuen Parameter $\varphi=t-\tfrac{5}{4}\pi$ ein, so ergibt sich (Beweis: Additionstheoreme):

$x={\tfrac {1}{\sqrt {2}}}\cos(2\varphi )\,\cos \varphi$

$y={\tfrac {1}{\sqrt {2}}}\cos(2\varphi )\,\sin \varphi$

Hieran lässt sich die einfache Polardarstellung

$r=\frac{1}{\sqrt{2}}\cos(2\varphi), \ 0\le \varphi <2\pi$

ablesen.

Die orthoptische Kurve einer Astroide ist ein Vierblatt (Quadrifolium).

Isoptische Kurven von Parabel, Ellipse und Hyperbel

Isoptische Kurven (lila) einer Parabel für die Winkel 80 bzw. 100 Grad

Isoptische Kurven (lila) einer Ellipse für die Winkel 80 und 100 Grad

Isoptische Kurven (lila) einer Hyperbel für die Winkel 80 und 100 Grad

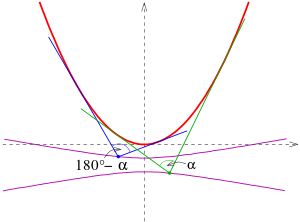
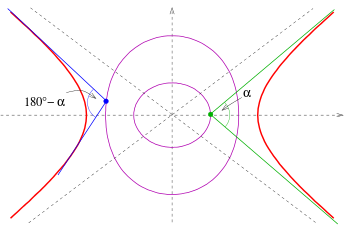
Im Folgenden werden die isoptischen Kurven zu einem Schnittwinkel $\alpha \neq 90^{\circ }$ angegeben und als $\alpha$ -isoptische Kurven bezeichnet. Zu den Beweisen s. unten.

Gleichungen der isoptischen Kurven

Parabel

Die $\alpha$ -isoptischen Kurven der Parabel mit der Gleichung y=ax^2 sind die Äste der Hyperbel

$x^{2}-\tan ^{2}\alpha \;(y+{\frac {1}{4a}})^{2}-{\frac {y}{a}}=0.$

Die beiden Äste der Hyperbel liefern die isoptischen Kurven für die beiden Winkel $\alpha ,180^{\circ }-\alpha$ (s. Bild).

Ellipse

Die $\alpha$ -isoptischen Kurven der Ellipse mit der Gleichung $\tfrac{x^2}{a^2}+\tfrac{y^2}{b^2}=1$ sind Teile der Kurve 4. Grades

$\tan ^{2}\alpha \;(x^{2}+y^{2}-a^{2}-b^{2})^{2}=4(a^{2}y^{2}+b^{2}x^{2}-a^{2}b^{2})$ (s. Bild).

Hyperbel

Die $\alpha$ -isoptischen Kurven der Hyperbel mit der Gleichung $\tfrac{x^2}{a^2}-\tfrac{y^2}{b^2}=1$ sind Teile der Kurve 4. Grades

$\tan ^{2}\alpha \;(x^{2}+y^{2}-a^{2}+b^{2})^{2}=4(a^{2}y^{2}-b^{2}x^{2}+a^{2}b^{2}).$

Die isoptischen Kurven von Ellipse und Hyperbel sind spirische Kurven.

Beweise

Parabel

Eine Parabel y=ax^2 lässt sich durch die Tangentensteigung m=2ax parametrisieren:

$\vec c(m)=\left(\frac{m}{2a},\frac{m^2}{4a}\right), \, m \in \R$

Die Tangente mit der Steigung hat die Gleichung

$y=mx-{\frac {m^{2}}{4a}}.$

Ein Punkt $(x_{0},y_{0})$ liegt auf der Tangente, wenn

$y_{0}=mx_{0}-{\frac {m^{2}}{4a}}$

gilt, das heißt, die Steigungen $m_{1},m_{2}$ der beiden Tangenten durch $(x_{0},y_{0})$ erfüllen die quadratische Gleichung

$m^{2}-4ax_{0}m+4ay_{0}=0.$

Damit der Schnittwinkel der beiden Tangenten $\alpha$ oder $180^{\circ }-\alpha$ ist, muss

$\tan^2\alpha = \left(\frac{m_1-m_2}{1+m_1m_2}\right)^2$

gelten. Löst man die quadratische Gleichung für setzt die beiden Lösungen $m_{1},m_{2}$ in die letzte Gleichung ein, ergibt sich nach Beseitigung der Nenner, die $x_{0},y_{0}$ enthalten, die Gleichung

$x_0^2-\tan^2\alpha\;\left(y_0+\frac{1}{4a}\right)^2-\frac{y_0}{a}=0.$

Dies ist die obige Hyperbelgleichung, deren Äste die beiden isoptischen Kurven der Parabel zu den Winkeln $\alpha$ und $180^{\circ }-\alpha$ sind.

Ellipse

Für eine Ellipse ${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$ kann man den Ansatz für die orthoptische Kurve bis zur quadratischen Gleichung

$m^{2}-{\frac {2x_{0}y_{0}}{x_{0}^{2}-a^{2}}}m+{\frac {y_{0}^{2}-b^{2}}{x_{0}^{2}-a^{2}}}=0$

übernehmen. Hier muss man, wie im Parabelfall, die quadratische Gleichung lösen, die Lösungen $m_{1},m_{2}$ in die Gleichung $\tan ^{2}\alpha =({\tfrac {m_{1}-m_{2}}{1+m_{1}m_{2}}})^{2}$ einsetzen und die Nenner beseitigen. Es ergibt sich die behauptete Gleichung 4. Grades:

$\tan^2\alpha \left(x_0^2+y_0^2-a^2-b^2\right)^2 = 4\left(a^2y_0^2+b^2x_0^2-a^2b^2\right)$

Hyperbel

Die Lösung für den Hyperbelfall ergibt sich aus dem Ellipsenfall durch die Ersetzung von $b^{2}$ durch $-b^{2}$ (wie bei den orthoptischen Kurven, siehe oben).

Bemerkung: Zur Visualisierung der Kurven siehe implizite Kurve.

Basierend auf einem Artikel in:

Wikipedia.de