Schnittwinkel (Geometrie)

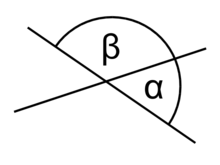
Schnittwinkel zwischen zwei Geraden

Ein Schnittwinkel ist in der Geometrie ein Winkel, den zwei sich schneidende Kurven oder Flächen bilden. Beim Schnitt zweier Geraden entstehen im Allgemeinen vier Schnittwinkel, von denen je zwei gegenüberliegende kongruent sind. Als Schnittwinkel wird meist der kleinere dieser beiden kongruenten Winkel bezeichnet, der dann spitz- oder rechtwinklig ist. Da Nebenwinkel sich zu 180° ergänzen, lässt sich der größere Schnittwinkel, der dann stumpf- oder rechtwinklig ist, aus diesem ermitteln.

Schnittwinkel zwischen den Graphen zweier reeller Funktionen lassen sich mittels der Ableitungen der Funktionen am Schnittpunkt berechnen. Schnittwinkel zwischen zwei Kurven kann man über das Skalarprodukt der Tangentialvektoren am Schnittpunkt ermitteln. Der Schnittwinkel zwischen einer Kurve und einer Fläche ist der Winkel zwischen dem Tangentialvektor der Kurve und dem Normalenvektor der Fläche am Schnittpunkt. Der Schnittwinkel zweier Flächen ist der Winkel zwischen den Normalenvektoren der Flächen und dann abhängig vom Punkt auf der Schnittkurve.

Schnittwinkel von Funktionsgraphen

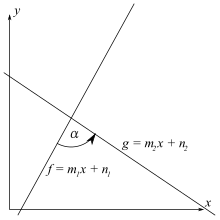
Schnittwinkel zwischen den Graphen zweier linearer Funktionen

Der Schnittwinkel $\alpha$ zwischen den Graphen zweier linearer Funktionen mit den Steigungen $m_{1}$ bzw. $m_{2}$ berechnet sich mittels

$\tan \alpha = \left|\frac{m_1 - m_2}{1+m_1m_2}\right|$ .

Die Herleitung dieser Formel erfolgt über die Additionstheoreme der trigonometrischen Funktionen. Gilt für die Steigungen m_1 m_2 = -1 , dann wird die Tangensfunktion unendlich und die beiden Geraden schneiden sich rechtwinklig.

Allgemeiner lässt sich auf diese Weise auch der Schnittwinkel zwischen den Graphen zweier differenzierbarer Funktionen mit den Ableitungen $m_{1}$ bzw. $m_{2}$ im Schnittpunkt ermitteln.

Beispiele

Die Graphen der beiden linearen Funktionen $f(x)=\sqrt{3}x+4$ und $g(x)=\tfrac{1}{\sqrt{3}}x-1$ schneiden sich an der Stelle $x=-\tfrac{5}{2}\sqrt{3}$ in einem $30^{\circ }$ -Winkel, denn

$\tan \alpha = \left| \frac{\sqrt{3}-\tfrac{1}{\sqrt{3}}}{1+\sqrt{3}\cdot\tfrac{1}{\sqrt{3}}} \right| = \frac{1}{\sqrt{3}} \Rightarrow \alpha = \arctan \frac{1}{\sqrt{3}} = 30^\circ$ .

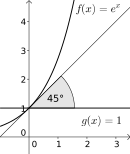
Die Exponentialfunktion f(x)=e^x schneidet die konstante Funktion g(x)=1 an der Stelle x=0 in einem Winkel von 45°, denn

$\tan \alpha = \left|\frac{f'(0) - g'(0)}{1+f'(0) \cdot g'(0)}\right| = \left|\frac{1 - 0}{1+1 \cdot 0}\right| = 1 \Rightarrow \alpha = \arctan 1 = 45^\circ$ .

Schnittwinkel von Kurven und Flächen

Schnittwinkel zweier Kurven

Der Schnittwinkel zweier (hier kreisförmiger) Kurven ist der Winkel zwischen den Tangenten der Kurven und am Schnittpunkt .

Im euklidischen Raum kann man den Schnittwinkel $\alpha$ zweier sich schneidender Geraden mit den Richtungsvektoren ${\vec {x}}$ und ${\vec {y}}$ durch

$\cos \alpha = \frac{| \vec x \cdot \vec y |}{| \vec x | \, | \vec y |}$

berechnen, wobei $\vec x \cdot \vec y$ das Skalarprodukt der beiden Vektoren und $| \vec x |$ die euklidische Norm eines Vektors ist. Allgemeiner lässt sich so auch der Schnittwinkel zweier differenzierbarer Kurven über das Skalarprodukt der zugehörigen Tangentialvektoren ${\vec {x}}$ und ${\vec {y}}$ am Schnittpunkt ermitteln.

Beispiele

Der Schnittwinkel zwischen zwei sich schneidenden Raumgeraden mit den Richtungsvektoren $\vec x=(1, 4, 5)^T$ und $\vec y=(2, 1, 3)^T$ ist

$\cos \alpha = \frac{| 1 \cdot 2 + 4 \cdot 1 + 5 \cdot 3 |}{\sqrt{1^2+4^2+5^2} \, \sqrt{2^2+1^2+3^2}} = \frac{21}{\sqrt{42} \, \sqrt{14}} = \frac{3}{2\sqrt{3}} \Rightarrow \alpha = \arccos\frac{3}{2\sqrt{3}} = 30^\circ$ .

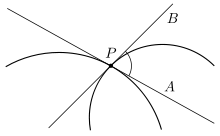
Um den Schnittwinkel zwischen der Gerade $\sqrt{3}x - y = 1$ und dem Einheitskreis $x^{2}+y^{2}=1$ im Punkt $(\tfrac{\sqrt{3}}{2}, \tfrac{1}{2})$ zu berechnen ermittelt man die beiden Tangentialvektoren in diesem Punkt als $\vec x = (1, \sqrt3)$ und $\vec y = (-\tfrac{1}{2}, \tfrac{\sqrt{3}}{2})$ und damit

$\cos \alpha = \frac{| 1 \cdot (-\tfrac{1}{2}) + \sqrt3 \cdot \tfrac{\sqrt{3}}{2} |}{\sqrt{1+3} \, \sqrt{\tfrac14 + \tfrac34}} = \frac{| -\tfrac12 + \tfrac32 |}{2 \cdot 1} = \frac12 \Rightarrow \alpha = \arccos\frac12 = 60^\circ$ .

Schnittwinkel einer Kurve mit einer Fläche

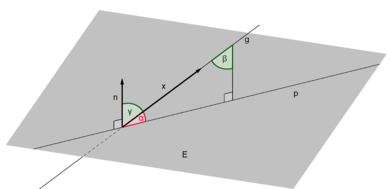
Schnittwinkel $\alpha$ , Gerade g, Ebene E, Projektionsgerade p
${\begin{aligned}&\,\gamma =\beta =90^{\circ }-\alpha \\\Rightarrow \,&\sin(\alpha )=\sin(90^{\circ }-\gamma )=\cos(\gamma )={\frac {|n\cdot x|}{|n||x|}}\end{aligned}}$

Der Schnittwinkel $\alpha$ zwischen einer Gerade mit dem Richtungsvektor ${\vec {x}}$ und einer Ebene mit dem Normalenvektor ${\vec {n}}$ ist durch

$\sin \alpha = \frac{| \vec{n} \cdot \vec{x} |}{| \vec{n} | \, | \vec{x} |}$

gegeben. Allgemeiner kann man so auch den Schnittwinkel zwischen einer differenzierbaren Kurve und einer differenzierbaren Fläche über das Skalarprodukt des Tangentialvektors der Kurve ${\vec {x}}$ mit dem Normalenvektor der Fläche ${\vec {n}}$ am Schnittpunkt berechnen. Dieser Schnittwinkel ist dann gleich dem Winkel zwischen dem Tangentialvektor der Kurve und dessen Orthogonalprojektion auf die Tangentialebene der Fläche.

Schnittwinkel zweier Flächen

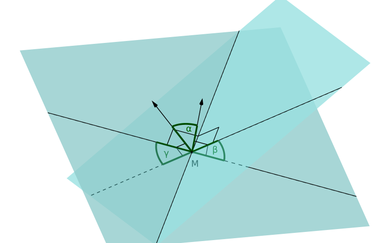
Schnittwinkel zwischen zwei Ebenen: $\alpha =\beta =\gamma$

Der Schnittwinkel $\alpha$ zwischen zwei Ebenen mit den Normalenvektoren ${\vec {n}}$ und $\vec{m}$ ist entsprechend

$\cos \alpha = \frac{| \vec{n} \cdot \vec{m}|}{| \vec{n} | \, | \vec{m} |}$ .

Allgemeiner lässt sich so auch der Schnittwinkel zwischen zwei differenzierbaren Flächen ermitteln. Dieser Schnittwinkel hängt dabei im Allgemeinen von dem Punkt auf der Schnittkurve ab.

Siehe auch

Literatur

Rolf Baumann: Geometrie: Winkelfunktionen, Trigonometrie, Additionstheoreme, Vektorrechnung. Mentor 1999, ISBN 3580636367.
Andreas Filler: Elementare Lineare Algebra. Springer, 2011, ISBN 9783827424136.

Basierend auf einem Artikel in:

Wikipedia.de