Pol und Polare

Pol und Polare sind ein Begriffspaar in der ebenen Geometrie der Kegelschnitte: Jedem Punkt der Ebene wird eine Gerade umkehrbar eindeutig zugeordnet. Vermittelndes Element ist ein Kegelschnitt. Die Gerade heißt Polare des Punktes, der Punkt Pol der Geraden. Die durch die Zuordnung Pol↔Polare gegebene Abbildung wird als Polarität, genauer als hyperbolische projektive Polarität bezeichnet.

Außen liegender Pol

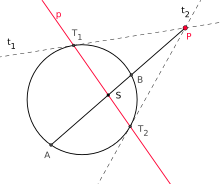
Pol (rot) außerhalb des Kreises mit Polare (rot)
harmonische Teilung: ${\frac {|AS|}{|BS|}}={\frac {|AP|}{|BP|}}$

Zu einem Punkt ${P}$ , der im Äußeren^[1] eines nicht entarteten Kegelschnitts (im Bild: eines Kreises) liegt, gibt es stets zwei Tangenten $t_{1}$ und $t_{2}$ , die durch ${P}$ gehen. Berühren diese den Kegelschnitt in den Punkten $T_{1}$ und $T_{2}$ , so heißt die Gerade $p=T_{1}T_{2}$ „die Polare zu ${P}$ (bezüglich des gegebenen Kegelschnitts)“.

Umgekehrt kann man sagen:

Schneidet eine Gerade {p} (die Polare) einen Kegelschnitt in zwei Punkten ${T_{1}}$ und ${T_{2}}$ , so heißt der Schnittpunkt der beiden Tangenten in ${T_{1}}$ und ${T_{2}}$ der Pol zu {p} (bezüglich des Kegelschnittes).

Harmonische Teilung und endgültige Definition

Zeichnet man durch den Pol ${P}$ eine Sekante, die den Kegelschnitt in {A} und ${B}$ und die Polare in ${S}$ schneidet, so teilen die Punkte ${S}$ und ${P}$ die Strecke ${\left[AB\right]}$ harmonisch (siehe Zeichnung). Dies erlaubt es, die Polare auch folgendermaßen zu definieren:

„Zeichnet man durch einen Punkt ${P}$ (den Pol) die Sekanten zu einem nicht entarteten Kegelschnitt, so liegen die vierten harmonischen Punkte, die (zusammen mit ${P}$ ) die ausgeschnittenen Sehnen harmonisch teilen, auf einer Geraden. Diese Gerade heißt die Polare zu ${P}$ (bezüglich des Kegelschnitts).“

Bei dieser Definition wird nicht mehr vorausgesetzt, dass ${P}$ im Äußeren des Kegelschnitts liegt. Auch zu jedem Punkt im Innern gibt es danach eine wohl definierte Polare.

Innen liegender Pol

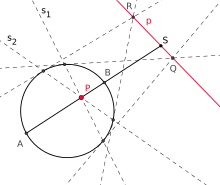
Pol (rot) innerhalb des Kreises mit Polare (rot)
harmonische Teilung: ${\frac {|AS|}{|BS|}}={\frac {|AP|}{|BP|}}$

Geometrisch erhält man die Polare zu einem Punkt ${P}$ im Innern eines Kegelschnitts, indem man (mindestens zwei) Sekanten durch ${P}$ zeichnet (im Bild ${s_1}$ und ${s_2}$ ) und an den Endpunkten ihrer Sehnen jeweils die Tangenten konstruiert. Die Schnittpunkte dieser Tangenten (im Bild {Q} und ${R}$ ) liegen auf der Polaren.

Umgekehrt kann man auch sagen:

Ist die Polare Passante des Kegelschnitts, so schneiden sich die Polaren aller auf ihr liegenden Punkte im Pol der Geraden.

Sonderfälle

Liegt der Pol auf der Kegelschnittlinie, so ist die Polare die Tangente in diesem Punkt. (Oder umgekehrt: Ist die Polare Tangente an den Kegelschnitt, so ist ihr Pol der Berührpunkt.)
Die Polare des Mittelpunkts ist die unendlich ferne Gerade.
Pol zu einem Durchmesser ist ein unendlich ferner Punkt, und zwar der, dessen Richtung die (parallelen!) Tangenten am Ende des Durchmessers angeben.

Zusammenhang mit der Kreisspiegelung

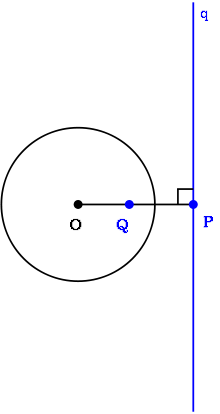
Die Polare zu einem Punkt bezüglich eines Kreises lässt sich, falls der Punkt nicht Mittelpunkt des Kreises ist, auch durch eine Kreisspiegelung bestimmen.

Die Zuordnung zwischen einem Pol und seiner Polaren bezüglich eines Kreises um weist dem Punkt ( $Q\neq O$ ) die Gerade zu, die durch den Spiegelpunkt $P=\sigma (Q)$ bei der Kreisspiegelung $\sigma$ an geht und auf der Verbindungsgerade senkrecht steht. Vergleiche dazu die Abbildung rechts unten.

Höhere Dimensionen

Im dreidimensionalen Raum tritt an die Stelle des Kegelschnitts als vermittelndes Element eine Fläche zweiter Ordnung, im einfachsten Fall also eine Kugel. Ist der Pol ein äußerer Punkt, so gibt es von ihm aus nicht nur zwei Tangenten, sondern im Allgemeinen eine ganze Schar von Tangenten, die einen Kegel (nicht notwendig einen Kreiskegel!) bilden. Dieser berührt die Fläche zweiter Ordnung in einer Linie (genauer: in einem Kegelschnitt – bei der Kugel in einem Kreis), und diese Linie ist die Schnittline der Fläche zweiter Ordnung mit einer Ebene – eben der Polarebene. Dieser Begriff ersetzt hier also den Begriff Polare.

Durch den Pol verlaufende Sekanten erzeugen auch hier eine harmonische Teilung, und man kann, auch für Punkte im Innern der Fläche zweiter Ordnung, ganz analog zum zweidimensionalen Fall definieren:

„Zeichnet man durch einen Punkt ${P}$ (den Pol) die Sekanten zu einer nicht entarteten Fläche zweiter Ordnung, so liegen die vierten harmonischen Punkte, die (zusammen mit ${P}$ ) die ausgeschnittenen Sehnen harmonisch teilen, auf einer Ebene. Diese Ebene heißt die Polebene zu ${P}$ (bezüglich der Fläche zweiter Ordnung).“

Auch die Sonderfälle verhalten sich analog.

Entsprechende Begriffsbildungen sind auch für Räume mit mehr als drei Dimensionen möglich.

Pol-Polare-Beziehung bei Kegelschnitten

Kegelschnitt	Gleichung	Polare des Punktes
Kreis	$x^{2}+y^{2}=r^{2}$	$x_{0}x+y_{0}y=r^{2}$
Ellipse	$\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1$	${\frac {x_{0}x}{a^{2}}}+{\frac {y_{0}y}{b^{2}}}=1$
Hyperbel	$\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$	${\frac {x_{0}x}{a^{2}}}-{\frac {y_{0}y}{b^{2}}}=1$
Parabel	$y=ax^{2}$	$y+y_{0}=2ax_{0}x$

Kegelschnitt	Gleichung	Pol der Gerade u x + v y = w
Kreis	$x^{2}+y^{2}=r^{2}$	$({\frac {r^{2}u}{w}},\;{\frac {r^{2}v}{w}})$
Ellipse	$\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1$	$({\frac {a^{2}u}{w}},\;{\frac {b^{2}v}{w}})$
Hyperbel	$\left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1$	$({\frac {a^{2}u}{w}},\;{\frac {-b^{2}v}{w}})$
Parabel	$y=ax^{2}$	$({\frac {-u}{2av}},\;{\frac {-w}{v}})$

Literatur

Hermann Schaal: Lineare Algebra und analytische Geometrie. 2. durchgesehene Auflage. Band 1. Vieweg, Braunschweig 1976, ISBN 3-528-03056-9.
Karl Rohn, Erwin Papperitz: Lehrbuch der Darstellenden Geometrie. 1. Auflage. Band 1. Salzwasser Verlag, Paderborn 2011, ISBN 978-3-86195-888-8.

Anmerkungen

↑ Bei einer Parabel oder Hyperbel liegt der Punkt im „Äußeren“, wenn sich die Kurve von ihm wegkrümmt, wenn sie also von dem Punkt aus gesehen konvex ist.

Basierend auf einem Artikel in:

Wikipedia.de