Gestreckte Exponentialfunktion

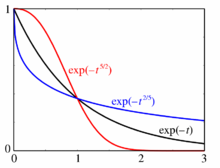
Gestreckte Exponentialfunktion $\beta ={\mbox{2/5}}=0{,}4$ (blau); gewöhnliche Exponentialfunktion mit $\beta =1$ (schwarz); gestauchte Exponentialfunktion mit $\beta ={\mbox{5/2}}=2{,}5$ (rot).

Die als gestreckte Exponentialfunktion bezeichnete mathematische Funktion ist eine Verallgemeinerung der Exponentialfunktion mit einem zusätzlichen Parameter $\beta >0$ im Exponenten:

$\phi (t)=e^{{-\left(t/\tau \right)^{\beta }}}$

oder, mit $\alpha =\tau ^{{-\beta }}$ :

$\phi (t)=e^{{-\alpha \,t^{\beta }}}$ .

In den meisten Anwendungen ist $\beta <1$ , was mit der namensgebenden Streckung einhergeht: Die Funktion fällt langsamer ab als die gewöhnliche Exponentialfunktion mit $\beta =1$ . Für $\beta >1$ erhält man die gestauchte Exponentialfunktion, für $\beta =2$ die Gaußfunktion. Anwendung ist unter anderem die Weibull-Verteilung.

Die gestreckte Exponentialfunktion wurde 1854 von Rudolf Kohlrausch eingeführt, um die Relaxation der elektrischen Polarisation eines Kondensators mit Glasdielektrikum zu beschreiben.

Die gestreckte Exponentialfunktion wird auch als Kohlrausch-Funktion oder Kohlrausch-Williams-Watts-Funktion, nach Graham Williams und David C. Watts bezeichnet, die diese 1970 wieder entdeckten.

Basierend auf einem Artikel in:

Wikipedia.de