
Weibull-Verteilung
| Weibull-Verteilung | |
Dichtefunktion 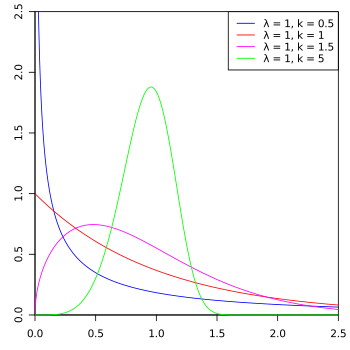 Dichtefunktion für verschiedene Formparameter
Dichtefunktion für verschiedene Formparameter | |
Verteilungsfunktion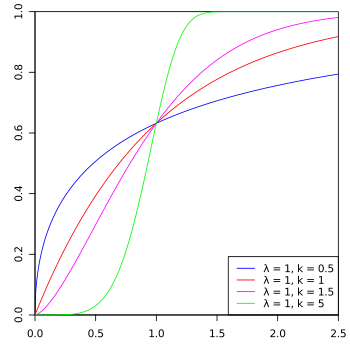 Verteilungsfunktion Verteilungsfunktion | |
| Parameter | |
|---|---|
| Träger | |
| Dichtefunktion | |
| Verteilungsfunktion | |
| Erwartungswert | |
| Varianz | |
Die Weibull-Verteilung (nach Waloddi Weibull, 1951) ist eine zweiparametrige Familie von stetigen Wahrscheinlichkeitsverteilungen über der Menge der positiven reellen Zahlen. Abhängig von ihren beiden Parametern ähnelt sie einer Normalverteilung oder asymmetrischen Verteilungen wie der Exponentialverteilung. Sie wird unter anderem zur statistischen Modellierung von Windgeschwindigkeiten oder zur Beschreibung der Lebensdauer und Ausfallhäufigkeit von elektronischen Bauelementen oder (spröden) Werkstoffen herangezogen. Anders als eine Exponentialverteilung berücksichtigt sie die Vorgeschichte eines Objekts, sie ist gedächtnisbehaftet und berücksichtigt die Alterung eines Bauelements nicht nur mit der Zeit, sondern in Abhängigkeit von seinem Einsatz. Sie lässt sich an steigende, konstante und fallende Ausfallraten technischer Systeme anpassen. Benannt ist die Verteilung nach dem schwedischen Ingenieur und Mathematiker Waloddi Weibull. Eine besondere Bedeutung hat sie in der Ereigniszeitanalyse.
Definition
Die Weibull-Verteilung hat zwei Parameter.
Skalenparameter
Der Skalenparameter
ist .
In manchen Anwendungen, insbesondere bei Zeitabhängigkeiten wird
durch seinen Kehrwert, die
charakteristische Lebensdauer
,
ersetzt.
ist bei Lebensdauer-Analysen jene Zeitspanne, nach der ca. 63,2 % der
Einheiten ausgefallen sind.
Dieser Wert ist eine Kenngröße der Weibull-Verteilung.
.
Wird kein Skalenparameter angegeben, so ist implizit
gemeint.
Formparameter
Der Formparameter
oder Weibull-Modul ist der Parameter .
Alternativ werden gerne die Buchstaben
oder
verwendet.
In der Praxis typische Werte liegen im Bereich .
Durch den Formparameter
lassen sich verschiedene speziellere Wahrscheinlichkeitsverteilungen
realisieren:
- Für
ergibt sich die Exponentialverteilung mit konstanter Ausfallrate.
- Für
ergibt sich die Rayleigh-Verteilung.
- Für
ergibt sich eine Verteilung mit verschwindender Schiefe (ähnlich der Normalverteilung).
Dichtefunktion, Verteilungsfunktion, Überlebensfunktion und Ausfallrate
Gegeben sei eine Weibull-Verteilung
mit Parametern .
Die Dichtefunktion ist
Die Verteilungsfunktion ist
Die Überlebensfunktion oder Zuverlässigkeitsfunktion, ist
Die Ausfallrate ist
Abweichende Parametrisierung
Eine andere verbreitete Konvention ist die Parametrisierung durch ,
d.h., die Weibull-Verteilung wird definiert als Verteilung mit den
Parameter
und der Dichtefunktion
Diese Darstellung wird häufig in der statistischen Theorie und in
Statistikprogrammen verwendet, da bei dieser Parametrisierung
ein Skalenparameter
ist.
Eigenschaften
Erwartungswert
Der Erwartungswert der Weibull-Verteilung ist
mit der Gammafunktion
.
Varianz
Die Varianz der Verteilung ist
.
Schiefe
Die Schiefe der Verteilung ist
mit dem Mittelwert
und der Standardabweichung
.
Entropie
Die Entropie der Weibull-Verteilung (ausgedrückt in nats) beträgt
wobei
die Euler-Mascheroni-Konstante
bezeichnet.
Anwendungen
Bei Systemen mit unterschiedlichen Ausfallursachen wie beispielsweise technischen Komponenten lassen sich diese mit drei Weibull-Verteilungen so abbilden, dass sich eine „Badewannen-Kurve“ ergibt Die Verteilungen decken dann diese drei Bereiche ab:
- Frühausfälle mit
, beispielsweise in der Einlaufphase („Kinderkrankheiten“).
- Zufällige Ausfälle mit
in der Betriebsphase
- Ermüdungs- und Verschleißausfälle am Ende der Produktlebensdauer mit
In der mechanischen Verfahrenstechnik findet die Weibull-Verteilung Anwendung als eine spezielle Partikelgrößenverteilung. Hier wird sie allerdings als Rosin-Rammler-Verteilung oder Rosin-Rammler-Sperling-Bennet-Verteilung (kurz RRSB-Verteilung) bezeichnet.
Für
gehört die Verteilung zu den Verteilungen
mit schweren Rändern, deren Dichte langsamer als exponentiell abfällt.
Weibullnetz
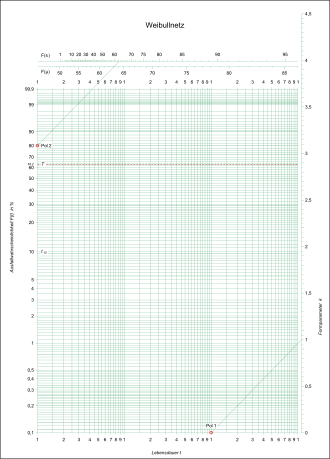
Trägt man die Verteilung in der Form
in einem doppelt logarithmischen Diagramm auf, welches auch als
Weibullnetz bezeichnet wird, ergibt sich eine Gerade, bei der man
den Parameter
leicht als Steigung ablesen kann. Die
charakteristische Lebensdauer
kann dann folgendermaßen bestimmt werden:
.
Hierbei bezeichnet
den y-Achsenabschnitt.
Oft kommt es vor, dass trotz Beanspruchung erst nach einer anfänglichen
Betriebszeit
Ausfälle eintreten (beispielsweise infolge des Verschleiß von Bremsbelägen).
Dies kann in der Weibull-Verteilungsfunktion berücksichtigt werden. Sie hat dann
folgendes Aussehen:
Trägt man die Funktion wieder auf, ergibt sich keine Gerade, sondern eine
nach oben konvexe Kurve. Verschiebt man alle Punkte um den Wert ,
so geht die Kurve in eine Gerade über.
Windgeschwindigkeit
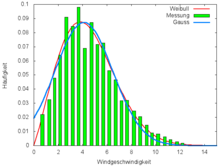
Die Grafik zeigt beispielhaft eine Messreihe von Windgeschwindigkeiten
(grün). Ein Gauß-Fit (blau) nähert sich den Zahlen nur ungenügend. Weder gibt es
negative Windgeschwindigkeiten noch ist die Verteilung symmetrisch. Eine
Weibull-Verteilung führt einen zweiten freien Parameter ein. Durch sie wird die
Verteilung für große und kleine Windgeschwindigkeiten sehr gut approximiert,
ebenso die Werte um das Maximum. Aus den Fitparametern
und
folgt ein Erwartungswert von 4,5 m/s, in guter Übereinstimmung mit dem Wert
von 4,6 m/s bestimmt aus den Messwerten.
Beziehung zu anderen Verteilungen
Beziehung zur Exponentialverteilung
- Man sieht, dass der Fall
die Exponentialverteilung
ergibt. Mit anderen Worten: Die Exponentialverteilung behandelt Probleme mit konstanter Ausfallrate
. Untersucht man jedoch Fragestellungen mit steigender (
) oder fallender (
) Ausfallrate, dann geht man von der Exponentialverteilung zur Weibull-Verteilung über.
- Ist der Parameter
, dann wird ein System mit einer mit der Zeit ansteigenden Ausfallrate, also ein alterndes System, beschrieben.
- Besitzt
eine Exponentialverteilung
mit Parameter
, dann besitzt die Zufallsvariable
eine Weibull-Verteilung
. Zum Beweis betrachte man die Verteilungsfunktion von
:
.
Das ist die Verteilungsfunktion einer Weibull-Verteilung.
Gestreckte Exponentialfunktion
Die Funktion
wird als gestreckte Exponentialfunktion bezeichnet.
Literatur
- Bernard W. Lindgren: Statistical Theory. Chapman & Hall, New York u.a. 1993, ISBN 0-412-04181-2.
- Marek Fisz: Wahrscheinlichkeitsrechnung und mathematische Statistik. Deutscher Verlag der Wissenschaften, Berlin 1970.
- Joachim Hartung, Bärbel Elpelt, Karl-Heinz Klösener: Statistik. Oldenbourg, München 2002, ISBN 3-486-25905-9.
- Horst Rinne, Hans-Joachim Mittag: Statistische Methoden der Qualitätssicherung. Hanser, München/Wien 2002, ISBN 3-446-15503-1.
- Holger Wilker: Weibull-Statistik in der Praxis, Leitfaden zur Zuverlässigkeitsermittlung technischer Produkte. BoD, Norderstedt 2010, ISBN 978-3-8391-6241-5.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 24.12. 2022