Arithmetisch-geometrisches Mittel

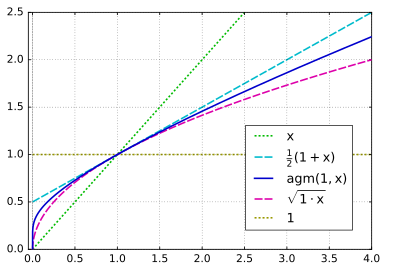
Plot des arithmetisch-geometrischen Mittels $\operatorname {agm} (1,x)$ (in dunkelblau)

In der Mathematik bezeichnet man als arithmetisch-geometrisches Mittel zweier positiver reeller Zahlen eine gewisse Zahl, die zwischen dem arithmetischen Mittel und dem geometrischen Mittel liegt.

Definition

Es seien und zwei nichtnegative reelle Zahlen. Ausgehend von ihnen werden induktiv zwei Folgen $a_{n}$ und $b_{n}$ mit

$a_{0}=a$

(1a)

$b_{0}=b$

(1b)

definiert:

$a_{n+1}={\frac {a_{n}+b_{n}}{2}}$

(2)

(arithmetisches Mittel)

$b_{n+1}={\sqrt {a_{n}b_{n}}}$

(3)

(geometrisches Mittel)

Die Folgen $a_{n}$ und $b_{n}$ konvergieren gegen einen gemeinsamen Grenzwert $M(a,b)$ , der als arithmetisch-geometrisches Mittel von und bezeichnet wird.

Dass die beiden Grenzwerte tatsächlich existieren und darüber hinaus sogar noch gleich sind, wird weiter unten in „Wichtige Eigenschaften“ gezeigt.

Einfaches Beispiel

Sei

$a_{0}=4$ und $b_{0}=9$

(4a,b)

Dann ist

$a_{1}={\frac {4+9}{2}}=6{,}5$ und $b_{1}={\sqrt {4\cdot 9}}=6$

(5)

$a_{2}=6{,}25\,$ und $b_{2}\approx 6{,}245\,$

(6)

$a_{3}\approx b_{3}\approx M(a,b)\approx 6{,}2475\,$

(7)

Einfache Eigenschaften

Für zwei nichtnegative Werte und gilt:

$M(a,b)=M(b,a)\,$

(10)

$M(ta,tb)=t\cdot M(a,b)$ für $t\geq 0$

(11)

Das heißt, das arithmetisch-geometrische Mittel ist – wie jede Mittelwertfunktion – symmetrisch und homogen vom Grad 1 in seinen beiden Variablen und .

$\min\{a,b\}\leq {\sqrt {ab}}\leq M(a,b)\leq {\frac {a+b}{2}}\leq \max\{a,b\}$

(12)

Gleichheit gilt dabei genau für a=b

$M(a,b)=M\left({\frac {a+b}{2}},{\sqrt {ab}}\right)$

(13)

Wichtige Eigenschaften

Monotonie: Für zwei positive Startwerte $0<b_{0}<a_{0}$ gilt nach der Ungleichung vom arithmetischen und geometrischen Mittel stets auch $b_{n}<a_{n}$ . Die Folge $b_{0},b_{1},b_{2},\dotsc$ ist also monoton wachsend und durch $a_{0}$ nach oben beschränkt, deshalb konvergiert sie gegen einen Grenzwert $\beta$ . Andererseits ist die Folge $a_{0},a_{1},a_{2},\dotsc$ monoton fallend und nach unten beschränkt, das heißt, sie konvergiert gegen einen Grenzwert $\alpha$ . Oder anders geschrieben:

$b_{0}<b_{1}<\dotsb <b_{n}<b_{n+1}<\dotsb <\beta \leq \alpha <\dotsb <a_{n+1}<a_{n}<\dotsb <a_{1}<a_{0}.$

(14)

Geht man nun in der Definitionsgleichung $a_{n+1}=(a_{n}+b_{n})/2$ zum Grenzwert über (das ist erlaubt, weil alle Grenzwerte existieren), dann erhält man $\alpha =(\alpha +\beta )/2$ , woraus $\alpha =\beta$ folgt. Somit sind die beiden Grenzwerte gleich und es ist $\alpha =\beta =M(a,b)$ das arithmetisch-geometrische Mittel.

Konvergenzgeschwindigkeit: Sei

$c_{n}:={\sqrt {{a}_{n}^{2}-{b}_{n}^{2}}}$

(15)

Wegen der Abschätzung

$c_{n+1}={\frac {1}{2}}(a_{n}-b_{n})={\frac {{c}_{n}^{2}}{4{a}_{n+1}}}\leq {\frac {{c}_{n}^{2}}{M(a,b)}}$

(16)

liegt ein Verfahren mit quadratischer Konvergenz vor.

Alternative Darstellung

Man kann beide Folgen auch voneinander "entkoppeln": Sei

$a_{0}=a$ , $b_{0}=b$ , $a_{1}={\frac {a_{0}+b_{0}}{2}}$ und $b_{1}={\sqrt {a_{0}b_{0}}}$ .

(21)

Dann kann man die obigen Gleichungen umformen zu:

$a_{n}={\frac {a_{n-1}\;+{\sqrt {(2a_{n-1}-a_{n-2})\cdot a_{n-2}}}}{2}}$

(22)

$b_{n}={\sqrt {\frac {b_{n-1}\cdot (b_{n-1}^{2}+b_{n-2}^{2})}{2b_{n-2}}}}$

(23)

Historisches

Das arithmetisch-geometrische Mittel wurde unabhängig voneinander von den Mathematikern Carl Friedrich Gauß und zuvor schon von Adrien-Marie Legendre entdeckt. Sie nutzten es, um die Bogenlänge von Ellipsen, also elliptische Integrale, näherungsweise zu berechnen. Gauß etwa notierte zum Zusammenhang zwischen dem arithmetisch-geometrischen Mittel und dem elliptischen Integral 1. Gattung (Bogenlänge einer Lemniskate) die Gleichung

${\frac {\pi }{2M(1,{\sqrt {2}})}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}$

(24)

in sein Mathematisches Tagebuch.^[1]

Verfahren von Salamin und Brent

Das nachfolgende Verfahren zur Berechnung der Kreiszahl $\pi$ wurde 1976 unabhängig voneinander von Richard P. Brent und Eugene Salamin publiziert. Es nutzt wesentlich die Erkenntnisse von Gauß über das arithmetisch-geometrische Mittel. Gauß bemerkte zu seiner Zeit allerdings nicht, dass sich damit auch ein schneller Algorithmus zur Berechnung der Zahl $\pi$ konstruieren lässt. Dennoch wird das Verfahren oft auch als Methode von Gauß, Brent und Salamin bezeichnet.

Die Schritte des Verfahrens können folgendermaßen beschrieben werden:

Initialisierung: Man verwendet als Startwerte

$a_{0}=1\qquad b_{0}={\frac {1}{\sqrt {2}}}\qquad s_{0}={\frac {1}{2}}\qquad$

(31)

Schleife: Für

$n=1,2,...$

berechnet man

$a_{n}={\frac {a_{n-1}+b_{n-1}}{2}}\,$

(32)

$b_{n}={\sqrt {a_{n-1}b_{n-1}}}\,$

(33)

$c_{n}=a_{n}^{2}-b_{n}^{2}\,$

(34)

$s_{n}=s_{n-1}-2^{n}c_{n}\,$

(35)

$p_{n}={\frac {2a_{n}^{2}}{s_{n}}}\,$

(36)

Die Folge der $(p_{n})$ konvergiert quadratisch gegen $\pi$ , das heißt, dass mit jedem Durchlaufen der Schleife sich die Zahl der korrekt berechneten Ziffern etwa verdoppelt. Damit konvergiert dieser Algorithmus deutlich schneller gegen $\pi$ als viele klassische Verfahren.

Zahlenbeispiel

Mit den Startwerten

$a_{0}=1\qquad b_{0}={\frac {1}{\sqrt {2}}}\approx 0{,}707106781186547\qquad s_{0}={\frac {1}{2}}=0{,}5\qquad$

(37)

berechnet man iterativ:

$a_{n}$	$b_{n}$	$c_{n}$	$s_{n}$	$p_{n}$
1	0,70710 67811 86547		0,5
0,85355 33905 93274	0,84089 64152 53715	0,02144 66094 06726	0,45710 67811 86547	3,18767 26427 12110
0,84722 49029 23494	0,84720 12667 46891	0,00004 00497 56187	0,45694 65821 61801	3,14168 02932 97660
0,84721 30848 35193	0,84721 30847 52765	0,00000 00001 39667	0,45694 65810 44462	3,14159 26538 95460

Nach drei Iterationen erhält man für das arithmetisch-geometrische Mittel den Näherungswert $M(1,1/{\sqrt {2}})\approx a_{3}\approx 0{,}847213084.$

Für die Zahl $\pi$ ergibt sich die Näherung $\pi \approx p_{3}\approx 3{,}141592653.\,$

Beziehung zu elliptischen Integralen

Es gilt:

${\frac {\pi /4}{M(a,b)}}=\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {(1-t^{2})((a+b)^{2}-(a-b)^{2}t^{2})}}}$

(41)

Die rechte Seite ist ein vollständiges elliptisches Integral erster Art.

Anmerkungen

↑ Vgl. Carl Friedrich Gauß: Mathematisches Tagebuch 1796–1814. Mit einer historischen Einführung von Kurt-R. Biermann. Durchgesehen und mit Anmerkungen versehen von Hans Wußing und Olaf Neumann. 5. Auflage. Harri Deutsch, Frankfurt am Main 2005. (Ostwalds Klassiker der exakten Wissenschaften, Band 256.), Nr. 98 (Braunschweig, 30. Mai 1798): „Terminum medium arithmetico-geometricum inter 1 et ${\sqrt {2}}$ esse $={\frac {\pi }{\varpi }}$ usque ad figuram undecimam comprobavimus, qua re demonstrata prorsus novus campus in analysi certo aperietur.“ „Wir haben bis zur elften Stelle nachgewiesen, daß der Wert des arithmetisch-geometrischen Mittels zwischen 1 und ${\sqrt {2}}={\frac {\pi }{\varpi }}$ ist; durch diesen Beweis wird uns ganz gewiß ein völlig neues Feld in der Analysis eröffnet werden.“ Dabei ist $\varpi :=2\int _{0}^{1}{\frac {dt}{\sqrt {1-t^{4}}}}$ die von Gauß eingeführte lemniskatische Konstante.

Basierend auf einem Artikel in:

Wikipedia.de