Substitution (Mathematik)

Unter Substitution versteht man in der Mathematik allgemein das Ersetzen eines Terms durch einen anderen mit dem Ziel der Überführung des Ausgangsterms in eine einfach lösbare Standardform. Die Substitution wird unter anderem verwendet, um biquadratische Gleichungen zu lösen oder um Integrale mittels Substitution zu bestimmen.

Beispiel

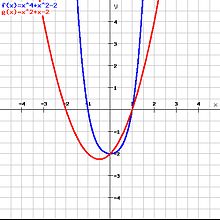
Funktionsgraphen vor und nach der Substitution

Folgendes Beispiel nutzt die Substitution, um die Lösungsmenge einer gegebenen biquadratischen Gleichung bzw. die Nullstellen einer ganzrationalen Funktion bzw. eines Polynoms 4. Grades zu bestimmen.

Die Gleichung

$x^{4}+x^{2}-2=0$

lässt sich durch die Substitution $t:=x^{2}$ in

$t^{2}+t-2=0$

überführen. Diese quadratische Gleichung lässt sich nun mit Standardverfahren wie zum Beispiel mit der p-q-Formel lösen. Man erhält als Lösungen $t_{1}=1$ und $t_{2}=-2$ . Durch Rücksubstitution erhält man für die Gleichungen

mit den Lösungen x_1 = 1 und $x_{2}=-1$ sowie

mit den komplexen Lösungen $x_{3}=i{\sqrt {2}}$ und $x_{4}=-i{\sqrt {2}}$ . Die Ausgangsgleichung hat somit als Lösungsmenge $\{1,-1\}$ in $\mathbb {R}$ bzw. $\{1,-1,i{\sqrt 2},-i{\sqrt 2}\}$ in $\mathbb {C}$ .

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de