Dreiachsiges Ellipsoid
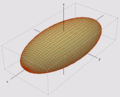
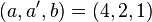
Bei einem dreiachsigen Ellipsoid ist – im Gegensatz zu einem Rotationsellipsoid (abgeplattetes bzw. verlängertes Ellipsoid) – der Äquator nicht hinreichend genau kreis-, sondern ellipsenförmig. Das dreiachsige Ellipsoid ist daher kein Rotationskörper und besitzt - wie der Name schon sagt - drei definierende Parameter, üblicherweise:
- zwei Äquatorhalbachsen (a, a′), die senkrecht aufeinander aufeinander stehen, und
- der Polradius b oder die Abplattung f.
Anwendung im Vermessungswesen
Ein dreiachsiges Ellipsoid bedeutet im Vergleich zum Rotationsellipsoid eine etwas bessere Anpassung an das Geoid, aber auch eine deutlich komplizierte Anwendung. In der Geodäsie werden die beiden Äquator-Halbachsen auch als Elliptizität des Erdäquators bezeichnet; diese macht bei der Erdfigur allerdings weniger als 100 Meter aus. Aus diesem Grund wurde das Krassowski-Ellipsoid, das ursprünglich als dreiachsiges Ellipsoid konzipiert war, auf zwei Parameter reduziert.
Deutlich dreiachsig ist hingegen die Form des Planeten Mars. Die Unterschiede betragen etwa 20 km, sodass für genaueste Ortsangaben (areografische Koordinaten) ein Rotationsellipsoid nicht ganz ausreicht.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 31.07. 2021