Fokalkegelschnitt
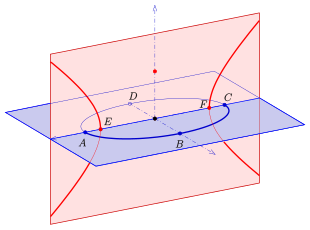
A,C: Hauptscheitel der Ellipse und Brennpunkte der Hyperbel
E,F: Brennpunkte der Ellipse und Scheitel der Hyperbel
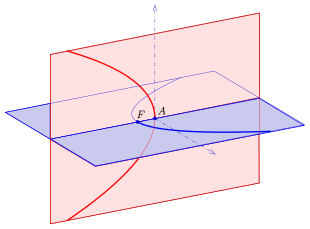
A: Scheitel der roten Parabel und Brennpunkt der blauen Parabel
F: Brennpunkt der roten Parabel und Scheitel der blauen Parabel
In der Geometrie sind Fokalkegelschnitte ein Kurvenpaar bestehend aus entweder
- einer Ellipse und einer Hyperbel, wobei die Hyperbel in einer zur Ellipsenebene senkrechten Ebene liegt und deren Scheitel die Brennpunkte der Ellipse und deren Brennpunkte die Hauptscheitel der Ellipse sind (siehe Bild).
oder
- zwei Parabeln in zueinander senkrechten Ebenen, wobei der Scheitel der einen der Brennpunkt der anderen ist.
Fokalkegelschnitte ergeben sich in natürlicher Weise bei der Beantwortung der Frage „Welche Rotationskegel enthalten als Schnitt eine vorgegebene Ellipse bzw. Hyperbel bzw. Parabel?“ (siehe unten)
Weiterhin spielen sie in der Geometrie eine wesentliche Rolle
- bei der Erzeugung von Dupinschen Zykliden. Sie sind dort Leitkurven für die Darstellung einer Zyklide als Kanalfläche.
- bei der Fadenkonstruktion von 3-achsigen Ellipsoiden.
In der physikalischen Chemie verwendet man Fokalkegelschnitte (engl.: focal conics) bei der Beschreibung von geometrischen Eigenschaften von Flüssigkristallen.
Man sollte Fokalkegelschnitte nicht mit konfokalen Kegelschnitten verwechseln. Bei letzteren haben alle Kegelschnitte dieselben Brennpunkte.
Gleichungen und Parameterdarstellungen
Ellipse und Hyperbel
- Gleichungen
Beschreibt man die Ellipse in der x-y-Ebene wie üblich durch die Gleichung
genügt die zugehörige Fokalhyperbel in der x-z-Ebene der Gleichung
wobei
die lineare Exzentrizität
der Ellipse ist, d.h. es gilt
- Parameterdarstellungen
- Ellipse:
und
- Hyperbel:
Zwei Parabeln
Zwei Parabeln in der x-y-Ebene bzw. x-z-Ebene:
- 1. Parabel:
und
- 2. Parabel:
Dabei ist
der Halbparameter
der beiden Parabeln.
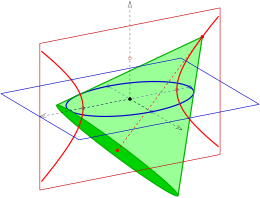
Rotationskegel durch eine Ellipse bzw. eine Hyperbel
- Die Spitzen der Rotationskegel durch eine vorgegebene Ellipse (Hyperbel) liegen auf der zur Ellipse (Hyperbel) gehörenden Fokalhyperbel (Fokalellipse).
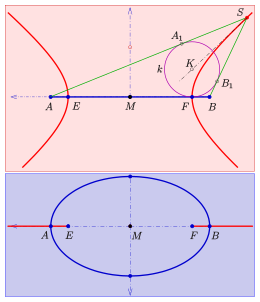
k: Dandelinsche Kugel (lila, Mittelpunkt K)
- Nachweis
Gegeben: Ellipse mit Hauptscheitel
und Brennpunkten
und ein die Ellipse enthaltender Rotationskegel (im Bild grün) mit Spitze
.
Aus Symmetriegründen muss die Rotationsachse des Kegels in der zur
Ellipsenebene senkrechten Ebene durch die Hauptachse der Ellipse liegen. Es gibt
eine Dandelinsche
Kugel ,
die die Ellipsenebene in dem Brennpunkt
und den Kegel in einem Kreis berührt. Mit Hilfe des Bildes und der Tatsache,
dass alle tangentialen Abstände eines Punktes von einer Kugel gleich sind,
erkennt man:
Also ist:
und die Menge aller möglichen Kegelspitzen
liegen auf der Hyperbel mit den Scheiteln
und den Brennpunkten
.
Lässt man die Kegelspitze ins Unendliche wandern, geht der Kegel in einen Zylinder über mit der Asymptote der Hyperbel als Achse und mit der kleinen Ellipsenhalbachse (= kleine Hyperbelhalbachse) als Radius.
Analog beweist man den Fall, dass eine Hyperbel gegeben ist.
Schnitt der Kegel durch Fokalkegelschnitte
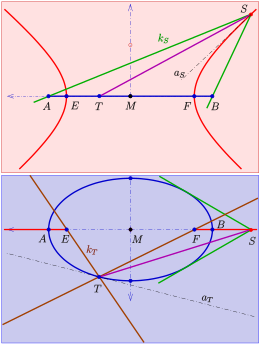
Die einem Paar von Fokalkegelschnitten zugeordneten senkrechten Kreiskegel durch die Kegelschnitte (s. vorigen Abschnitt) spielen bei der Anwendung des Satzes von Dupin auf Dupinsche Zykliden eine wichtige Rolle. Denn es gilt
- Wählt man einen beliebigen Punkt
der Hyperbel und einen beliebigen Punkt
der Ellipse und ist
der Kreiskegel (grün) durch die Ellipse mit Spitze
und
der Kreiskegel (braun) durch die Hyperbel mit Spitze
, so schneiden sich beide Kegel in der gemeinsamen Gerade
senkrecht.
Der Schlüssel zum Beweis liegt in der Tatsache, dass die Kegelachse
von
die Tangente an die Hyperbel im Punkt
ist. Analog gilt: Die Achse
des Kegels
ist Tangente an die Ellipse in
.
Beide Aussagen folgen aus den Brennstrahleigeneschaften einer Ellipse
bzw. Hyperbel
(siehe Bild).
Da es sich um senkrechte Kreiszylinder handelt, genügt es zu zeigen, dass die
Normalebenen der Kegel durch
sich orthogonal schneiden:
Ist
und
, so ist
und
.
Es gilt:
(s. oben).
Es ist nachzuweisen, dass die Normalenvektoren der beiden Normalebenen senkrecht zueinander stehen, d.h., dass
ist.
Beim Nachrechnen kann man das Kreuzprodukt mit Hilfe der Lagrange-Identität vermeiden:
Literatur
- Georg Glaeser, Hellmuth Stachel, Boris Odehnal: The Universe of Conics, Springer, 2016, ISBN 3662454505.
- E. Müller, E. Kruppa: Lehrbuch der darstellenden Geomelrie, Springer-Verlag, Wien, 1961, ISBN 978-3-211-80589-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.05. 2022