Spaltensummennorm

Illustration der Spaltensummennorm

Die Spaltensummennorm ist in der Mathematik die von der Summennorm abgeleitete natürliche Matrixnorm. Die Spaltensummennorm einer Matrix entspricht der maximalen Betragssumme aller ihrer Spalten. Sie ist submultiplikativ und mit der Summennorm verträglich. Die Spaltensummennorm wird insbesondere in der linearen Algebra und der numerischen Mathematik verwendet.

Definition

Die Spaltensummennorm $\|\cdot \|_{1}$ einer Matrix $A\in {\mathbb {K} }^{m\times n}$ mit $\mathbb {K}$ als dem Körper der reellen oder komplexen Zahlen ist die von der Summennorm abgeleitete natürliche Matrixnorm und damit definiert als

$\|A\|_{1}:=\max _{x\neq 0}{\frac {\|Ax\|_{1}}{\|x\|_{1}}}=\max _{\|x\|_{1}=1}\|Ax\|_{1}$ .

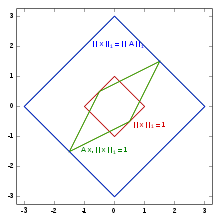
Anschaulich entspricht die Spaltensummennorm dem größtmöglichen Streckungsfaktor, der durch die Anwendung der Matrix auf einen Vektor mit Betragssumme Eins entsteht. Für die Spaltensummennorm gilt die namensgebende Darstellung

$\|A\|_{1}=\max _{\|x\|_{1}=1}\|Ax\|_{1}=\max _{\|x\|_{1}=1}\sum _{i=1}^{m}\left|\sum _{j=1}^{n}a_{ij}x_{j}\right|=\max _{j=1,\ldots ,n}\sum _{i=1}^{m}|a_{ij}|$ .

Hierbei wurde genutzt, dass die Summe innerhalb der Betragsstriche für festes für einen der Einheitsvektoren $x=\pm e_{j}$ mit $j=1,\ldots ,n$ maximal wird. Die Berechnung der Spaltensummennorm erfolgt also durch die Ermittlung der Betragssumme jeder Spalte und dann durch Auswahl des Maximums dieser Werte. Zur Unterscheidung von der verwandten Zeilensummennorm $\|\cdot \|_{\infty }$ hilft folgende Merkregel: die steht senkrecht und steht für die Spalten, während die $\infty$ waagrecht liegt und für die Zeilen steht.

Beispiele

Reelle Matrix

Die Spaltensummennorm der reellen (2 × 3)-Matrix

$A={\begin{pmatrix}1&{-2}&{-3}\\2&3&{-1}\end{pmatrix}}$

berechnet sich als

$\|A\|_{1}=\max\{|1|+|2|,|{-2}|+|3|,|{-3}|+|{-1}|\}=\max\{3,5,4\}=5$ .

Komplexe Matrix

Die Spaltensummennorm der komplexen (2 × 3)-Matrix

$A={\begin{pmatrix}1&-2i&3-i\\2i&3&-1-i\end{pmatrix}}$

berechnet sich als

$\|A\|_{1}=\max\{|1|+|2i|,|-2i|+|3|,|3-i|+|-1-i|\}=\max\{3,5,{\sqrt {10}}+{\sqrt {2}}\}=5$ .

Eigenschaften

Normeigenschaften

Die Normaxiome Definitheit, absolute Homogenität und Subadditivität folgen für die Spaltensummennorm direkt aus den entsprechenden Eigenschaften von natürlichen Matrixnormen. Insbesondere ist die Spaltensummennorm damit auch submultiplikativ und mit der Summennorm verträglich, das heißt, es gilt

$\|A\cdot x\|_{1}\leq \|A\|_{1}\cdot \|x\|_{1}$

für alle Matrizen $A\in {\mathbb {K} }^{m\times n}$ und alle Vektoren $x\in {\mathbb {K} }^{n}$ und die Spaltensummennorm ist die kleinste Norm mit dieser Eigenschaft.

Adjungierte

Für eine adjungierte Matrix $A^{H}\in {\mathbb {K} }^{n\times m}$ (im reellen Fall transponierte Matrix) gilt

$\|A^{H}\|_{1}=\max _{j=1,\ldots ,n}\sum _{i=1}^{m}|{\bar {a}}_{ji}|=\max _{i=1,\ldots ,n}\sum _{j=1}^{m}|a_{ij}|=\|A\|_{\infty }$ ,

wobei ${\bar {a}}$ die konjugiert komplexe Zahl zu mit dem gleichen Betrag ist. Die Spaltensummennorm einer adjungierten oder transponierten Matrix entspricht also der Zeilensummennorm der Ausgangsmatrix. Die Spektralnorm einer Matrix kann dadurch als geometrisches Mittel aus Zeilen- und Spaltensummennorm nach oben abgeschätzt werden.

Basierend auf einem Artikel in:

Wikipedia.de