
Blockmatrix
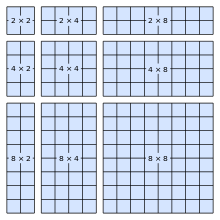
In der Mathematik bezeichnet eine Blockmatrix eine Matrix, die so interpretiert wird, als sei sie in mehrere Teile, genannt Blöcke zerlegt worden. Eine Blockmatrix kann auf intuitive Art und Weise als die Originalmatrix mit einer bestimmten Anzahl an horizontalen und vertikalen Trennstrichen dargestellt werden. Diese Trennstriche teilen die Originalmatrix in Untermatrizen auf.
Definition
Sei
eine Matrix der Größe
.
Die Zahl der Zeilen und der Spalten der Matrix werde nun mittels
und
ganzzahlig zerlegt, wobei
und
die Anzahl der Summanden bezeichnen. Dann lässt sich
darstellen als
mit Untermatrizen
der Größe
.
Jede
-Matrix
kann auf unterschiedliche Arten als Blockmatrix interpretiert werden, je nachdem
wie die
Zeilen und
Spalten zerlegt werden. Auf triviale Weise kann jede Matrix auch als Blockmatrix
mit nur einem Block oder als Blockmatrix mit
Blöcken der Größe
aufgefasst werden.
Beispiel
Die Matrix
kann in vier -Blöcke
zerlegt werden
Die zerlegte Matrix ergibt sich dann zu
Multiplikation von Blockmatrizen
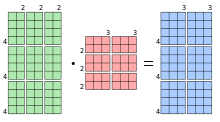
Das Produkt
von Blockmatrizen kann rein mit Operationen der Untermatrizen dargestellt
werden. Sei
eine
-Matrix
mit
Zeilenzerlegungen and
Spaltenzerlegungen
und
eine
-Matrix
mit
Zeilenzerlegungen und
Spaltenzerlegungen
dann gilt, dass das Produkt
blockweise berechnet werden kann, wobei
eine
-Matrix
mit
Zeilenzerlegungen und
Spaltenzerlegungen ist. Die Untermatrizen der Blockmatrix
sind gegeben durch
Oder, mithilfe der Einsteinschen Summenkonvention, welche implizit über mehrfach vorhandene Indizes summiert, kompakter dargestellt
Blockdiagonalmatrix
Eine Blockdiagonalmatrix ist eine quadratische Blockmatrix deren Hauptdiagonale
quadratische Blockmatrizen sind, und alle restlichen Blöcke Nullmatrizen sind. Eine
Blockdiagonalmatrix
hat die Form
wobei die Untermatrizen
quadratische Matrizen sind. Anders ausgedrückt ist
die direkte Summe von
,
das heißt
oder mit dem Formalismus von Diagonalmatrizen
.
Für die Determinante und die Spur einer Blockdiagonalmatrix gilt
und
.
Die Inverse
einer Blockdiagonalmatrix
ist wiederum eine Blockdiagonalmatrix, zusammengesetzt aus den Inversen der
einzelnen Blöcke
Die Eigenwerte
und Eigenvektoren einer Blockdiagonalmatrix entsprechen den (kombinierten)
Eigenwerten und Eigenvektoren der Untermatrizen .
Beispiel
Wichtige Beispiele für Blockdiagonalmatrizen sind Matrizen in Jordanscher Normalform. Die Blöcke sind in diesem Fall sogenannte Jordanblöcke, das sind Bidiagonalmatrizen, auf deren Hauptdiagonalen der Eigenwert des Blocks steht, während alle Elemente auf der Nebendiagonalen 1 sind.
Blocktridiagonalmatrix
Eine Blocktridiagonalmatrix ist eine andere spezielle Blockmatrix,
welche genau wie die Blockdiagonalmatrix eine quadratische Matrix ist,
allerdings zusätzlich mit quadratischen Blockmatrizen in den beiden ersten
(oberen und unteren) Nebendiagonalen.
Die restlichen Blöcke sind Nullmatrizen. Die Blocktridiagonalmatrix ist im
Grunde genommen eine Tridiagonalmatrix,
allerdings mit Blockmatrizen anstelle von Skalaren.
Eine Blocktridiagonalmatrix
hat die Form
wobei ,
und
jeweils quadratische Blockmatrizen auf der unteren Nebendiagonale, der
Hauptdiagonale und der oberen Nebendiagonale sind.
Blocktridiagonalmatrizen tauchen oft in numerischen Lösungen verschiedener Probleme auf (zum Beispiel in der numerischen Strömungsmechanik). Es existieren optimierte numerische Verfahren zur LR-Zerlegung von Blocktridiagonalmatrizen und dementsprechend effiziente Verfahren zur Lösung von Gleichungssystemen mit Triadiagonalmatrizen als Koeffizientenmatrix. Der Thomas-Algorithmus>, welcher zur effizienten Lösung von Gleichungssystemen mit Tridiagonalmatrix verwendet wird, kann auch auf Blocktridiagonalmatrizen angewendet werden.
Block-Toeplitz-Matrix
Eine Block-Toeplitz-Matrix ist eine andere spezielle Blockmatrix,
welche, ähnlich wie die Toeplitz-Matrix
wiederholt die gleichen Blöcke auf den Diagonalen enthält. Eine
Block-Toeplitz-Matrix
hat die Form
Siehe auch


© biancahoegel.de;
Datum der letzten Änderung: Jena, den: 24.01. 2024