Kantenfärbung
In der Graphentheorie ist eine Kantenfärbung eine Abbildung, die jeder Kante eines Graphen eine (abstrakte) Farbe zuordnet. Der Begriff ist eng verwandt mit der Knotenfärbung.
Definition
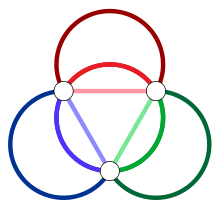
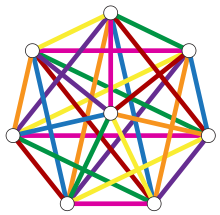
Für einen ungerichteten Multigraph
nennt man eine Abbildung
der Kantenmenge in die Menge
der natürlichen Zahlen eine Kantenfärbung von
.
Die Elemente aus
werden in diesem Zusammenhang Farben genannt. Man nennt
gültig oder zulässig, falls für je zwei beliebige benachbarte
Kanten
und
gilt, dass
.
Besitzt
eine Kantenfärbung
,
so dass höchstens k Farben im Bildbereich
von
auftreten, nennt man G k-kantenfärbbar.
Das kleinste ,
für das ein Graph
-kantenfärbbar
ist, heißt chromatischer Index, Kantenfärbungszahl oder auch
Kantenchromatische Zahl des Graphen
und wird meist mit
bezeichnet.
Eigenschaften
Nach dem Satz
von Vizing ist der chromatische
Index eines einfachen
Graphen
mindestens so groß wie sein Maximalgrad,
aber höchstens eins größer als dieser, also formal:
Graphen mit
nennt man Klasse‑1-Graphen, Graphen mit
nennt man Klasse‑2-Graphen (da die Abschätzung des Satzes nicht für
Multigraphen gilt, werden Multigraphen Klasse‑2-Graphen genannt, wenn
gilt). Zu entscheiden, ob ein Graph Klasse 1 oder Klasse 2 ist (Klassifizierungsproblem),
ist NP-vollständig.
Das heißt, obwohl der Maximalgrad leicht zu bestimmen ist und der chromatische
Index nur einen von zwei möglichen Werten annehmen kann, ist das Problem, für
einen gegebenen Graphen genau diesen einen Wert zu bestimmen, NP-schwer.
Für bipartite
Graphen ist .
Damit sind alle bipartiten Graphen Klasse‑1-Graphen.
Dualität zur Eckenfärbung
Die Bestimmung einer Kantenfärbung ist zur Bestimmung einer Eckenfärbung in
der Weise dual, dass eine Kantenfärbung eines Graphen
genau eine Knotenfärbung
des Kantengraphen
ist. Daraus folgt, dass
gilt. Die kantenchromatische Zahl eines Graphen ist also genau die chromatische
Zahl des Kantengraphen. Trotz dieses engen Zusammenhangs sind die Probleme
unterschiedlich schwer zu lösen und die verfügbaren Abschätzungen unterscheiden
sich deutlich.
Verallgemeinerungen
Eine wesentliche Verallgemeinerung der Kantenfärbung ist der Begriff der Listenfärbung. Hier wird für jede Kante (oder jeden Knoten) eine Liste mit verfügbaren Farben vorgegeben und der Graph soll nun eine gültige Kantenfärbung aus diesen Listen erhalten. Des Weiteren gibt es die Totalfärbung, bei der sowohl Knoten als auch Kanten gefärbt werden sollen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.05. 2021