
Bipartiter Graph
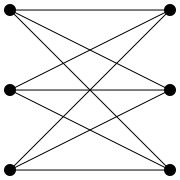
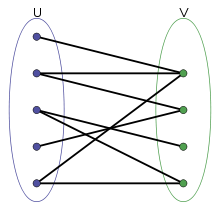
Ein bipartiter oder paarer Graph ist ein mathematisches Modell für Beziehungen zwischen den Elementen zweier Mengen. Es eignet sich sehr gut zur Untersuchung von Zuordnungsproblemen. Des Weiteren lassen sich für bipartite Graphen viele Grapheneigenschaften mit deutlich weniger Aufwand berechnen als dies im allgemeinen Fall möglich ist.
Definitionen
Ein einfacher
Graph
(V Menge der Knoten, E Menge der Kanten) heißt bipartit oder paar, falls sich
seine Knoten
in zwei disjunkte Teilmengen A und
B aufteilen lassen, sodass zwischen den Knoten innerhalb beider
Teilmengen keine Kanten
verlaufen. Das heißt für jede Kante
gilt entweder
und
oder
und
.
Die Menge
bezeichnet man dann als Bipartition des Graphen
und die Mengen
als Partitionsklassen. Vereinfacht dargestellt, ist ein bipartiter Graph
ein Graph, in dem zwei Gruppen von Knoten existieren, innerhalb derer keine
Knoten miteinander verbunden sind.
Der Graph
heißt vollständig bipartit, falls eine Bipartition
existiert, sodass jeder Knoten aus
mit jedem Knoten aus
verbunden ist. Einen solchen Graphen bezeichnet man auch als
,
wobei
und
jeweils die Anzahl der Knoten von
und
sind. Ein vollständig bipartiter Graph, bei dem
oder
ist, heißt Sterngraph.
Eigenschaften
- Die Paarungszahl entspricht der Knotenüberdeckungszahl.
- Die Partitionsklassen
sind schon nach Definition stabile Mengen.
- Der chromatische
Index entspricht seinem Maximalgrad.
Eine gültige Kantenfärbung lässt sich in
bestimmen.
- Jeder bipartite Graph ist 2-knotenfärbbar Jede Partitionsklasse bekommt also eine Farbe zugewiesen. Umgekehrt ist auch jeder 2-färbbare Graph bipartit.
- Ein regulärer bipartiter Graph besitzt ein perfektes Matching.
- Ein Graph ist genau dann bipartit, wenn er keinen Kreis ungerader Länge enthält.
- Alle bipartiten Graphen sind Klasse 1-Graphen, ihre Kantenchromatische Zahl entspricht also ihrem Maximalgrad.
- Für bipartite Graphen ist der Listenchromatische Index gleich dem chromatischen Index. Damit sind bipartite Graphen eine Klasse von Graphen, für welche die Listenfärbungsvermutung zutrifft.
- Für bipartite Graphen gilt
, wobei
die totalchromatische Zahl ist und
der Maximalgrad. Für bipartite Graphen gilt also die Totalfärbungsvermutung.
- Alle bipartiten Graphen sind perfekte Graphen, somit stimmt für jeden induzierten Teilgraphen die Cliquenzahl mit der chromatischen Zahl überein.
Algorithmen
Mit dem Algorithmus
von Hopcroft und Karp lässt sich in
eine größte Paarung finden und darüber auch die Stabilitätszahl
bestimmen.
Mit einem einfachen Algorithmus, der auf Tiefensuche basiert, lässt sich in linearer Zeit bestimmen, ob ein Graph bipartit ist, und eine gültige Partition bzw. 2-Färbung ermitteln. Dabei wird einem beliebigen Knoten eine Farbe, und seinen Kindern die jeweils komplementäre Farbe zugewiesen. Wird beim Färben festgestellt, dass zwei benachbarte Knoten die gleiche Farbe haben, ist der Graph nicht bipartit.
Anwendung
- Petri-Netz
- Heiratsproblem (Sekräterinnenproblem)
Verallgemeinerung
Ein k-partiter
Graph ist ein Graph, dessen Knotenmenge in
Partitionen unterteilt werden kann, sodass es keine Kante zwischen zwei Knoten
einer Partition gibt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.02. 2026