
Stabile Menge
Eine stabile Menge, unabhängige Menge oder Co-Clique ist in der Graphentheorie eine Teilmenge von Knoten eines Graphen, die zueinander nicht adjazent sind. Zu entscheiden, ob ein Graph eine stabile Menge einer bestimmten Mindestgröße enthält, wird Stabilitätsproblem genannt und gilt, wie das Finden einer größten stabilen Menge, als algorithmisch schwierig.
Definitionen
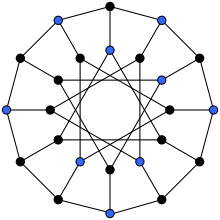
Stabile Menge
Sei
ein ungerichteter
Graph
ohne Mehrfachkanten und
eine Teilmenge von
.
Gilt für je zwei beliebige verschiedene Knoten
und
aus
,
dass sie nicht benachbart
sind, so nennt man
eine stabile bzw. unabhängige Menge des Graphen.
Maximale stabile Menge
Eine stabile Menge
von
nennt man maximal, wenn man keinen weiteren Knoten
aus
zu
hinzufügen kann, so dass
zusammen mit
eine stabile Menge ist. Gibt es in
keine stabile Menge, die mehr Elemente als
enthält, so nennt man
größte stabile Menge. Die Anzahl der Elemente einer größten stabilen
Menge nennt man Stabilitäts- oder Unabhängigkeitszahl. Statt über
Teilmengen von
definiert man stabile Mengen auch als spezielle Teilgraphen.
Äußerlich stabile Menge
Eine Teilmenge
von Knoten in einem gerichteten
Graphen
heißt äußerlich stabil oder dominierend, wenn jeder Knoten aus
einen positiven
Nachbarn in
hat. Die Mächtigkeit
einer kleinsten dominierenden Menge heißt Dominationszahl
des Graphen
.
Eine Menge von Knoten eines gerichteten Graphen heißt Kern des Graphen,
wenn sie zugleich stabil und dominierend ist.
Eigenschaft
Jede stabile Menge eines Graphen ist eine Clique im Komplementgraphen.
Probleme und Komplexität
Das Entscheidungsproblem zu einem Graphen G und einer natürlichen Zahl k zu entscheiden, ob G eine stabile Menge der Größe mindestens k enthält, wird Stabilitätsproblem genannt. Das zugehörige Optimierungsproblem fragt nach der Stabilitätszahl eines Graphen. Das zugehörige Suchproblem fragt nach einer größten stabilen Menge. Diese drei Probleme sind polynomiell äquivalent.
Das Stabilitätsproblem ist NP-vollständig, das zugehörige Optimierungs- und Suchproblem ist NP-äquivalent. Die NP-Schwere des Stabilitätsproblems lässt sich dabei leicht durch Reduktion des Cliquenproblems auf das Stabilitätsproblem zeigen, indem man den Komplementgraphen bildet.
In bipartiten Graphen lässt sich eine größte stabile Menge in polynomieller Zeit berechnen. Tatsächlich gilt sogar etwas stärker, dass die Stabilitätszahl in perfekten Graphen in polynomieller Zeit berechnet werden können. Die Berechnung einer maximalen stabilen Menge gelingt bereits mit einem einfachen Greedy-Algorithmus.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 01.11. 2020