
Komplementgraph
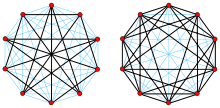
Als Komplementgraph, komplementären Graph oder Komplement bezeichnet man in der Graphentheorie einen speziellen Graphen, den man aus einem gegebenen Graphen erhält.
Dabei besitzt der komplementäre Graph die gleichen Knoten wie der Ursprungsgraph, unterscheidet sich aber in seinen Kanten: Der Komplementgraph besitzt genau die Kanten, die der Ursprungsgraph nicht hat.
Definition
Sei
ein ungerichteter
bzw. gerichteter
Graph
ohne Mehrfachkanten. Der ungerichtete bzw. gerichtete Graph ohne
Mehrfachkanten
heißt Komplementgraph von
,
wenn die Schnittmenge
von
und
leer ist und die Vereinigungsmenge
von
und
- im ungerichteten Fall die Menge aller 2-elementigen Teilmengen von V bzw.
- im gerichteten Fall das kartesische
Produkt
ergibt.
Der Komplementgraph eines gegebenen Graphen
wird häufig auch mit
bezeichnet. Als selbstkomplementär bezeichnet man Graphen, die isomorph zu
ihrem komplementären Graphen sind.
Eigenschaften
- Das Komplement des Komplementes von G ist G selbst.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.10. 2020