
Irreduzible Markow-Kette
Irreduzibilität ist ein Attribut für diskrete Markow-Ketten, welches vereinfacht aussagt, dass die Kette nicht in mehrere Einzelketten auf Teilmengen des ursprünglichen Zustandsraumes zerlegt (reduziert) werden kann. Irreduzibilität ist neben der Aperiodizität eine der wichtigen Eigenschaften von Markow-Ketten, die für die Konvergenz gegen eine stationäre Verteilung von Bedeutung ist. Da eine Markow-Kette stets durch einen Übergangsgraphen dargestellt werden kann, ist auch der äquivalente Begriff Transitivität gebräuchlich. Vereinfacht bedeutet Transitivität, dass es von jedem Zustand einen Weg in jeden anderen Zustand gibt.
Definition
Sei
eine (zeitlich homogene) Markow-Kette auf dem diskreten Zustandsraum
.
Dann heißt die Markow-Kette irreduzibel, genau dann, wenn es für alle
ein
gibt, so dass
Jeder Zustand muss also von jedem anderen Zustand mit positiver Wahrscheinlichkeit erreichbar sein.
Äquivalente Definitionen
Äquivalent sind:
- Die Markow-Kette ist irreduzibel
- Es ist
ist für alle Zustände
. Dabei ist
die Wartezeit vom Start in Zustand
bis zum erstmaligen Erreichen von
- Alle Zustände des Zustandsraumes kommunizieren miteinander.
- Jeder Zustand
ist von jedem anderen Zustand
aus erreichbar
- Es existiert nur eine Kommunikationsklasse
Ist der Zustandsraum endlich, so lässt sich die Liste erweitern um die folgenden Punkte:
- Der Übergangsgraph der Markow-Kette ist stark zusammenhängend.
- Die Übergangsmatrix, welche die Markow-Kette beschreibt, ist irreduzibel.
Manche Autoren definieren zuerst die irreduzibilität einer Teilmenge des Zustandsraumes (auch über die obigen Kriterien) und nennen dann die Markow-Kette irreduzibel, wenn der gesamte Zustandsraum eine irreduzible Menge ist.
Schwache Irreduzibilität
Außerdem gibt es noch den Begriff der schwachen Irreduzibilität. Eine Markow-Kette heißt genau dann schwach irreduzibel, wenn
gilt, wobei
die oben definierte Wartezeit ist.
Eigenschaften
- Irreduzible Markow-Ketten sind entweder periodisch oder aperiodisch, da alle Zustände dieselbe Periode besitzen.
- Irreduzible Markow-Ketten besitzen keine absorbierenden Zustände.
- Irreduzible Markow-Ketten sind entweder transient oder rekurrent, da diese Eigenschaft immer bei allen ihren Zuständen zugleich auftritt.
- Ist der Zustandsraum endlich und
die Übergangsmatrix der Markow-Kette, dann existiert folgendes Irreduzibilitäts-Kriterium: Existiert ein
, so dass
gilt, dann ist die Markow-Kette irreduzibel und aperiodisch. Dabei ist das Größer-Zeichen komponentenweise zu verstehen.
- Im Falle eines endlichen Zustandsraumes folgt aus Irreduzibilität positive Rekurrenz.
Beispiele
Man betrachte die auf dem Zustandsraum
durch die Übergangsmatrix
definierte Kette. Diese Kette springt, wenn sie sich im Zustand i befindet, mit 50-prozentiger Wahrscheinlichkeit nach i+1, sonst bleibt sie bei i (ist i=4, springt sie mit 50-prozentiger Wahrscheinlichkeit zurück zu 1). Offensichtlich kann die Kette von jedem Zustand aus innerhalb von drei Schritten zu jedem anderen Zustand gelangen, also sind alle Zustände miteinander verbunden. Diese Markow-Kette ist demnach irreduzibel.
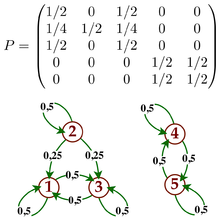
Ein weiteres Beispiel: Betrachte auf demselben Zustandsraum die Matrix
.
Hier gelangt man von Zustand 1 aus nur zu Zustand 3, und von diesem aus auch
wieder nur zur 1 zurück. Die Zustände 2 und 4 sind von 1 und 3 aus auch in
beliebig vielen Schritten nicht erreichbar und umgekehrt. S zerfällt hier also
in die Äquivalenzklassen
und
.
In diesem Beispiel lässt sich die Kette in zwei separate Ketten auf den beiden
Äquivalenzklassen und mit Matrizen
sowie
zerlegen.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 21.12. 2023