MCMC-Verfahren

Markow-Chain-Monte-Carlo-Verfahren (kurz MCMC-Verfahren; seltener auch Markow-Ketten-Monte-Carlo-Verfahren) sind eine Klasse von Algorithmen, die zufällige Stichproben aus Wahrscheinlichkeitsverteilungen (Monte-Carlo-Algorithmus) ziehen. Dies geschieht auf der Basis der Konstruktion einer Markow-Kette, welche die erwünschte Verteilung als ihre stationäre Verteilung aufweist. Der Zustand der Kette nach einer großen Zahl von Schritten wird dann als Stichprobe der erwünschten Verteilung benutzt. Die Qualität der Stichprobe steigt mit zunehmender Zahl der Schritte.

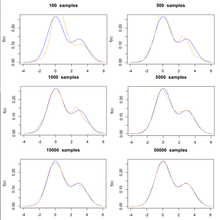
Konvergenz des Metropolis-Hastings-Algorithmus; die blaue Verteilung soll durch die orange approximiert werden.

Üblicherweise gelingt es leicht, eine Markow-Kette mit den erwünschten Eigenschaften zu konstruieren. Das Schwierigere ist, zu ermitteln, wie viele Schritte nötig sind, um Konvergenz zur stationären Verteilung mit akzeptablem Fehler zu erreichen, also den Algorithmus so zu gestalten, dass möglichst effektiv unabhängige Systemzustände generiert werden. Eine gute Kette mit einer gut gewählten Anfangsverteilung wird schnell konvergieren, d.h., die stationäre Verteilung wird schnell erreicht. Bei typischer Anwendung von MCMC-Verfahren kann die Zielverteilung nur näherungsweise erreicht werden, da es immer einen gewissen Resteffekt der Anfangsverteilung gibt. Stichproben, welche mit MCMC-Algorithmen generiert werden, weisen typischerweise hohe Autokorrelationen auf. Daher wird der Fehler des Mittelwerteschätzers bei Verwendung des Standardfehlers unterschätzt.

Anwendungsgebiete

Häufige Anwendungen dieser Algorithmen finden sich bei der numerischen Berechnung mehrdimensionaler Integrale. Diese finden sich z. B.

im Rahmen der bayesschen Statistik^[1] (z. B. bei Approximate Bayesian Computation)
in Computersimulationen in der statistischen Physik: MCMC-Verfahren können z. B. zur Simulation von Systemen im kanonischen Ensemble herangezogen werden. Simulationen nahe einem Phasenübergang konvergieren i.d.R. langsamer und erfordern eine längere Equilibrierung. Eine hinreichende, aber nicht notwendige Bedingung, dass ein MCMC-Verfahren den kanonischen Zustand als stationäre Verteilung aufweist, ist die Detailed-Balance-Eigenschaft.
oder zur Auswertung von Pfadintegralen in Quantenfeldtheorien^[2].

Beispiel

Angenommen, wir können eine diskrete Gleichverteilung auf $\{0,1\}$ simulieren. Dies entspricht dem Wurf einer fairen Münze mit $P(\{1\})=P(\{0\})=0{,}5$ , wobei „1=Kopf“ und „0=Zahl“ sein soll. Nun wollen wir aber eine Verteilung auf $S=\{1,2,3\}$ simulieren mit $P_{Z}(\{1\})=0{,}2$ und $P_{Z}(\{2\})=P_{Z}(\{3\})=0{,}4$ . Dazu definieren wir eine Markow-Kette, bei der alle Übergangswahrscheinlichkeiten simuliert werden können (sprich 0,5, 0 oder 1 sind) und die die Verteilung $P_{Z}$ als stationäre Verteilung hat. Folgendes Vorgehen bildet eine Markow-Kette, welche die Voraussetzungen erfüllt: Befindet man sich im Zustand 1, gehe nach 2. Befindet man sich im Zustand 2, wirf eine Münze. Zeigt sie Kopf, gehe zu 3, ansonsten verharre in der 2. Befindet man sich im Zustand 3, wirf eine Münze. Zeigt sie Kopf, gehe zu 1, ansonsten verharre in der 3. Diese Markow-Kette wird durch die folgende Übergangsmatrix beschrieben:

$M={\begin{bmatrix}0&1&0\\0&0{,}5&0{,}5\\0{,}5&0&0{,}5\end{bmatrix}}=((P(i|k))_{k,i})$ .

Da alle Einträge der Matrix $M^{t}>0$ positiv sind ab $t\geq 3$ , ist die Markow-Kette irreduzibel und aperiodisch. Daher konvergiert die Markow-Kette für jede beliebige Startverteilung $v_{0}$ gegen die stationäre Verteilung $\pi =P_{Z}$

Für die Simulation starten wir nun im Zustand 1. In der Tabelle findet sich jeweils der Simulationsschritt in der ersten Spalte, dann die exakte Aufenthaltswahrscheinlichkeit für den Zustand 1 in der 2. Spalte: $P(X_{k}=1)=\sum _{i=1}^{3}P(1|i)P(X_{k-1}=i)$

Diese konvergiert nach Voraussetzung gegen 0,2. In der letzten Spalte steht die relative Häufigkeit des Zustandes 1, gemittelt über eintausend Simulationen. Diese nähert sich nach mehreren Simulationsschritten der stationären Verteilung an. Lässt man also die Simulation lange laufen, so ist die so erhaltene Stichprobe $P_{Z}$ verteilt.

Schritte $k$	$P(X_{k}=1)$	Relative Häufigkeit der 1 in Tausend Simulationen
0	1	1
1	0	0
2	0	0
3	0,25	0,228
4	0,25	0,271
5	0,1875	0,173
6	0,1875	0,176
7	0,2031	0,236
8	0,2031	0,180
9	0,1992	0,202
10	0,1992	0,171
11	0,2002	0,205
12	0,2002	0,198
13	0,2000	0,190
14	0,2000	0,206

Normiert man die Summe der Einträge des linksseitigen Eigenvektors von $M$ zum Eigenwert 1, so erhält man die Wahrscheinlichkeiten der Zustände der stationären Wahrscheinlichkeitsverteilung der Markow-Kette: hier 0,2, 0,4, 0,4.

Algorithmen (Auswahl)

Siehe auch: Monte-Carlo-Algorithmus und Monte-Carlo-Simulation

Beispiele für MCMC-Verfahren sind:

Metropolis-Algorithmus: Das lokale Verfahren erzeugt Zufallsbewegungen, die mit einer gewissen Wahrscheinlichkeit akzeptiert oder zurückgewiesen werden. Es ist einfach zu implementieren, hat jedoch den Nachteil einer hohen Autokorrelation der erzeugten Systemzustände.
Gibbs-Sampling: Das lokale Verfahren ist ein Sonderfall des Metropolis-Hastings-Algorithmus, bei dem die Zustände entsprechend der lokalen Wahrscheinlichkeitsverteilung erzeugt werden.
Wärmebadalgorithmus
Hybrid-Monte-Carlo-Algorithmus: Das Verfahren stellt eine Kombination aus Molekulardynamik und Zufallsbewegung her. Die Molekulardynamik wird benutzt, um effizient neue, unabhängige Zustände zu erzeugen, die mit einer gewissen Wahrscheinlichkeit akzeptiert oder zurückgewiesen werden.
Clusteralgorithmen: Hierbei handelt es sich um spezielle, nicht-lokale Verfahren, die die Autokorrelationzeiten und damit das so genannte Critical Slowing down, bei Phasenübergängen, reduzieren. Ein solcher Algorithmus wurde erstmals 1987 von R. Swendsen und J.-S.Wang für ein Potts-Modell benutzt, siehe Swendsen-Wang-Algorithmus. Eine populäre Variante dieser Clustermethode ist der 1989 eingeführte Wolff-Algorithmus.
Over-Relaxation-Verfahren

Literatur

Siehe auch: Monte-Carlo-Simulation und Monte-Carlo-Algorithmus

Fachliteratur (Originalarbeiten)

N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller und E. Teller: Equation of State Calculations by Fast Computing Machines. In: Journal of Chemical Physics. Band 21, 1953, S. 1087–1092, doi: 10.1063/1.1699114 (englisch).
W. K. Hastings: Monte Carlo sampling methods using Markov chains and their applications. In: Biometrika. Band 57, Nr. 1, 1. April 1970, S. 97–109, doi: 10.1093/biomet/57.1.97 (englisch).
Robert H. Swendsen, Jian-Sheng Wang: Nonuniversal critical dynamics in Monte Carlo simulations. In: Physical Review Letters. Band 58, Nr. 2, 12. Januar 1987, S. 86–88, doi: 10.1103/PhysRevLett.58.86 (englisch).
Stephen L. Adler: Over-relaxation method for the Monte Carlo evaluation of the partition function for multiquadratic actions. In: Physical Review D. Band 23, Nr. 12, 15. Juni 1981, S. 2901–2904, doi: 10.1103/PhysRevD.23.2901 (englisch).

Fachbücher

Steve Brooks, Andrew Gelman, Galin Jones, Xiao-Li Meng (Hrsg.): Handbook of Markov Chain Monte Carlo. Chapman and Hall/CRC, 2011, ISBN 978-0-429-13850-8, doi: 10.1201/b10905 (englisch)
Jeff Gill: Bayesian Methods. 3. Auflage. Chapman and Hall/CRC, 2014, ISBN 978-1-4398-6249-0, doi: 10.1201/b17888 (englisch).

Einzelnachweise

↑ Sudipto Banerjee, Bradley P. Carlin, Alan E. Gelfand: Hierarchical Modeling and Analysis for Spatial Data. Chapman and Hall/CRC, 2014, ISBN 978-0-429-13717-4, doi: 10.1201/b17115 (englisch, taylorfrancis.com
↑ Ankur Gupta, James B. Rawlings: Comparison of parameter estimation methods in stochastic chemical kinetic models: Examples in systems biology. In: AIChE Journal. Band 60, Nr. 4, April 2014, S. 1253–1268, doi: 10.1002/aic.14409, PMID 27429455 (englisch).

Basierend auf einem Artikel in:

Wikipedia.de