Metropolis-Algorithmus

Der Metropolis-Algorithmus ist ein Markov-Chain-Monte-Carlo-Verfahren (MCMC) zur Erzeugung von Zuständen eines Systems entsprechend der Boltzmann-Verteilung. Der davon abgeleitete, allgemeinere Metropolis-Hastings-Algorithmus^[1] ermöglicht es, Folgen von Zufallsvariablen, genauer Markow-Ketten, zu simulieren, die eine gewünschte Verteilung als stationäre Verteilung besitzen, insbesondere in vielen Fällen, bei denen die Verteilungen der Zufallsvariablen nicht direkt simuliert werden können.

Metropolis-Algorithmus

Der Metropolis-Algorithmus wurde 1953 von Nicholas Metropolis, Marshall Rosenbluth, Edward Teller, Augusta H. Teller, Arianna W. Rosenbluth publiziert^[2] (zur Geschichte siehe auch Monte-Carlo-Simulation). Er wird dazu genutzt, eine Markow-Kette und damit die Zustände eines Systems entsprechend der Boltzmann-Verteilung zu erzeugen. Dabei hängt der neue Zustand des Systems $x_{i+1}$ nur vom vorherigen Zustand $x_{i}$ ab.

Im Folgenden wird der Algorithmus für den Fall beschrieben, dass das System von einem mehrdimensionalen Ort ${\vec {x}}$ abhängt. ${\vec {x}}$ sei kontinuierlich und der aktuelle Ort nach $i$ Iterationen wird mit ${\vec {x}}_{i}$ bezeichnet. Der Metropolis-Algorithmus ergibt sich dann durch Wiederholung der folgenden Schritte:

Ein neuer Ort ${\vec {y}}={\vec {x}}_{i}+r\cdot {\vec {q}}$ wird ausgewählt, wobei ${\vec {q}}$ ein Zufallsvektor aus Komponenten zwischen −1 und +1 und r ein fest gewählter Suchradius ist, das heißt, der neue Ortsvektor wird als Zufallsvektor in einer festen Umgebung von ${\vec {x}}_{i}$ gewählt, wobei die verschiedenen Komponenten der räumlichen Dimensionen nicht notwendigerweise gleich sein müssen.
Die Energie-Differenz wird berechnet und die neue Konfiguration mit der Wahrscheinlichkeit akzeptiert, wobei für die Temperatur des Systems und für die Boltzmann-Konstante steht.
Dies bedeutet:
- Ist $\Delta E\leq 0\,$ , die neue Position also energetisch gleichwertig oder günstiger, wird ${\vec {y}}$ in jedem Fall als neuer aktueller Ort akzeptiert, ${\vec {x}}_{i+1}={\vec {y}}$ .
- Ist $\Delta E>0\,$ , die neue Position also energetisch ungünstiger, wird ${\vec {y}}$ dagegen nur mit der Wahrscheinlichkeit $p_{\mathrm {A} }$ als neuer aktueller Ort akzeptiert, wozu man praktisch eine Zufallszahl q zwischen 0 und 1 bestimmt und anschließend mit $p_{\mathrm {A} }$ vergleicht: Ist q kleiner als $p_{\mathrm {A} }$ , wird ${\vec {y}}$ als neuer aktueller Ort akzeptiert, ${\vec {x}}_{i+1}={\vec {y}},$ andernfalls nicht, ${\vec {x}}_{i+1}={\vec {x}}_{i}$ .

Das oben beschriebene Verfahren lässt sich einfach auch auf andere Fälle wie beispielsweise diskrete Zustände übertragen. Für Systeme aus vielen wechselwirkenden Teilchen wird der Metropolis-Algorithmus dabei zunächst lokal für ein einzelnes Teilchen angewandt und anschließend – entweder nacheinander oder zufällig – auf alle Teilchen.

Eigenschaften

Autokorrelation

Kleine Werte für die Vorschlagsänderungen |r| führen dabei zu großen Akzeptanzraten, haben jedoch den Nachteil hoher Autokorrelationszeiten

$\tau =\sum _{i=0}^{\infty }\Gamma (i)=\sum _{i=0}^{\infty }\left\langle \left(A_{0}-\langle A\rangle \right)\left(A_{i}-\langle A\rangle \right)\right\rangle$

Große Werte von |r| dagegen verkürzen zwar die Autokorrelationszeit, haben dafür aber nun den Nachteil einer geringeren Akzeptanzrate, so dass in der Praxis stets ein Mittelweg gesucht werden muss.

Burn-In Phase

Da die Markovkette an einem beliebigen Punkt startet, welcher eventuell sehr unwahrscheinlich ist, sind die anfänglich vorgeschlagenen Zustände aufgrund der Autokorrelation immer noch unwahrscheinlich. Erst nach einer gewissen Zahl an akzeptierten Vorschlägen erreicht das Verfahren Zustände, welche „repräsentative“ Stichproben aus der stationären Verteilung sind. Daher werden anfänglich gezogene Stichproben verbrannt, sie stammen aus der „Burn-In Phase“. Zur Diagnostik der Konvergenz von Markovketten^[3], kann z. B. die Gelman-Rubin Diagnostik durchgeführt werden, bei der mehrere Markov-Ketten simuliert werden und durch Zusammenfassungsstatiken überprüft wird, ob diese Ketten zu ähnlichen Werten konvergiert sind. Während der Burn-In Phase unterscheiden sich die simulierten Markov-Ketten typischerweise deutlich in den Zusammenfassungsstatistiken.

Metropolis-Hastings-Algorithmus

W. Keith Hastings generalisierte 1970 das Verfahren.^[1] Der Metropolis-Hastings-Algorithmus kann Zustände für eine beliebige Wahrscheinlichkeitsverteilung $W({\vec {x}})$ erzeugen. Voraussetzung ist lediglich, dass die Dichte an jedem Ort ${\vec {x}}$ berechnet werden kann. Der Algorithmus benutzt eine Vorschlagsdichte $P({\vec {y}}\mid {\vec {x}})$ , die vom derzeitigen Ort ${\vec {x}}$ und möglichem nächsten Ort ${\vec {y}}$ abhängt. Beim Metropolis-Hastings-Algorithmus wird ein Vorschlag ${\vec {y}}$ anhand der Vorschlagsdichte zufällig erzeugt und mit der Wahrscheinlichkeit $p_{\mathrm {A} }=\min \left(1,{\frac {W({\vec {y}})P({\vec {x}}\mid {\vec {y}})}{W({\vec {x}})P({\vec {y}}\mid {\vec {x}})}}\right)$ akzeptiert.

Für eine Vorschlagsdichte, die symmetrisch ist ( $P({\vec {y}}\mid {\vec {x}})=P({\vec {x}}\mid {\vec {y}})$ ), sowie eine Boltzmann-Verteilung als Wahrscheinlichkeitsverteilung $W$ ergibt sich hieraus der ursprüngliche Metropolis-Algorithmus.

Anwendungen

Monte-Carlo-Simulation

→ Hauptartikel: Monte-Carlo-Simulation

Bei Monte-Carlo-Simulationen werden Konfigurationen mittels des Metropolis-Algorithmus erzeugt und Mittelwerte/Erwartungswerte physikalisch relevanter Größen berechnet, beispielsweise der Erwartungswert des Drucks oder der Dichte:

$\left\langle A\right\rangle =Z^{-1}\int [\mathrm {d} x]e^{-\beta E(x)}\,A(x)$

mit

$Z=\int [\mathrm {d} x]e^{-\beta E(x)}$

$\beta =(kT)^{-1}$

Dazu werden von den Iterationsschritten des Metropolis-Algorithmus zunächst so viele ausgeführt, bis sich das System hinreichend nah an das thermische Gleichgewicht angenähert hat, d.h. bis die Wahrscheinlichkeit der einzelnen Konfigurationen der Boltzmann-Verteilung entspricht. Befindet sich das System im thermischen Gleichgewicht, so entspricht die Wahrscheinlichkeitsverteilung $W(x)$ der Boltzmann-Verteilung, d.h. die Konfigurationen werden mit der Wahrscheinlichkeit $W(x)={\frac {1}{Z}}e^{-\beta E(x)}$ erzeugt (Importance Sampling) und es muss lediglich über jeden Messwert, bzw. Messwerte in konstantem Abstand, gemittelt werden: $\left\langle A\right\rangle =\lim _{N\to \infty }{\frac {1}{N}}\sum _{i=1}^{N}A(x_{i})$ .

Der Metropolis-Algorithmus erzeugt Systeme im kanonischen Zustand, d.h. mit konstanter Temperatur. Um mikrokanonische Zustände zu erzeugen, können Molekulardynamik-Algorithmen verwendet werden.

In der Originalarbeit von Nicholas Metropolis et al. wurde der Algorithmus für die Monte-Carlo-Simulation eines zweidimensionalen Harte-Scheiben-Modells verwendet. Der Algorithmus wurde später für eine Vielzahl unterschiedlichster Monte-Carlo-Simulationen in Bereichen wie z. B. bei der Thermodynamik bzw. der Statistischen Physik, Festkörperphysik, Quantenelektrodynamik oder Quantenchromodynamik eingesetzt. Dabei muss der Algorithmus gegebenenfalls angepasst werden; beispielsweise muss man die Energie durch den Hamiltonoperator oder die Wirkung ersetzen.

Der Metropolis-Algorithmus ist leicht zu implementieren, jedoch nicht immer der effizienteste Algorithmus. Alternativ können andere lokale oder nicht-lokale Verfahren Verwendung finden.

Optimierungsverfahren

Der Metropolis-Algorithmus kann auch als stochastisches Optimierungsverfahren zum Finden eines globalen Minimums einer Funktion verwendet werden. Hierzu wird mit einer hohen Temperatur begonnen, damit möglichst ein großes Gebiet der Wertelandschaft besucht wird. Anschließend wird die Temperatur langsam abgesenkt, sodass man sich mit immer höherer Wahrscheinlichkeit einem Minimum nähert. Ein solcher Metropolis-Algorithmus mit von der (Simulations-)Zeit abhängiger Temperatur heißt simulierte Abkühlung (simulated annealing). Für bestimmte Formen der simulierten Abkühlung konnte bewiesen werden, dass sie das globale Minimum einer Wertelandschaft finden.

Das Verfahren ähnelt dem Bergsteigeralgorithmus (hill climbing), akzeptiert jedoch im Gegensatz zu diesem auch Schritte weg vom nächsten Minimum, so dass das „Hängen bleiben“ in lokalen Minima vermieden wird, die noch nicht das absolute Minimum ergeben. Der Metropolis-Algorithmus überwindet so kleine Hügel, bevor weiter in Richtung Tal gegangen wird, da der Anstieg in Richtung Hügel klein ist und somit die Akzeptanzwahrscheinlichkeit relativ groß ist.

Bayessches Lernen

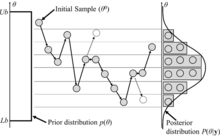
Ablauf des Metropolis-Hastings (M-H) Algorithmus für die Parameterschätzung mithilfe des Markov Chain Monte Carlo (MCMC) Ansatzes.

Zum Ziehen von Stichproben (engl. Sample) aus der Posterior-Verteilung wird folgende Akzeptanzwahrscheinlichkeit verwendet um von einem Zustand $\theta _{i}$ zu einem vorgeschlagenen Zustand $\theta ^{*}$ überzugehen: $P_{acc}(\theta _{i}\to \theta ^{*})=\min \left(1,{\frac {{\mathcal {L}}(y|\theta ^{*})P(\theta ^{*})}{{\mathcal {L}}(y|\theta _{i})P(\theta _{i})}}{\frac {Q(\theta _{i}|\theta ^{*})}{Q(\theta ^{*}|\theta _{i})}}\right),$ wobei ${\mathcal {L}}$ die Likelihood der Daten ist, $P(\theta )$ die Prior-Wahrscheinlichkeitsdichte und $Q$ die (bedingte) Vorschlagsdichte.

Literatur

Siehe auch: Monte-Carlo-Simulation, Monte-Carlo-Algorithmus und MCMC-Verfahren

Einzelnachweise

↑ ^{Hochspringen nach: a} ^b W. K. Hastings: Monte Carlo sampling methods using Markov chains and their applications. In: Biometrika. Band 57, Nr. 1, 1. April 1970, ISSN 1464-3510, S. 97–109, doi: 10.1093/biomet/57.1.97 (englisch, oup.com
↑ Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, Edward Teller: Equation of State Calculations by Fast Computing Machines. In: The Journal of Chemical Physics. Band 21, Nr. 6, 1. Juni 1953, ISSN 0021-9606, S. 1087–1092, doi: 10.1063/1.1699114 (englisch).
↑ Vivekananda Roy: Convergence Diagnostics for Markov Chain Monte Carlo. In: Annual Review of Statistics and Its Application. Band 7, Nr. 1, 9. März 2020, ISSN 2326-8298, S. 387–412, doi: 10.1146/annurev-statistics-031219-041300 (englisch, annualreviews.org

Basierend auf einem Artikel in:

Wikipedia.de