
Ergodentheorie
Die Ergodentheorie ist ein Teilgebiet der Mathematik, das sowohl der Maßtheorie und Stochastik als auch der Theorie dynamischer Systeme zugeordnet wird. Die Ursprünge der Ergodentheorie liegen in der statistischen Physik. Der Name leitet sich von griechischen έργον (Werk) und όδος (Weg) ab. Einzelheiten des physikalischen Begriffs siehe Ergodizität.
Vorbereitungen
Man nennt zu einem Wahrscheinlichkeitsraum
eine messbare
Abbildung
maßerhaltend,
falls das Bildmaß von
unter
wieder
ist, d.h.
für alle Mengen
aus der σ-Algebra
.
Entsprechend heißt das 4-Tupel
maßerhaltendes dynamisches System.
Eine Menge
heißt außerdem
-invariant,
falls sie mit ihrem Urbild übereinstimmt, wenn also
gilt. Das Mengensystem aller
-invarianten
Mengen
bildet hierbei eine σ-Algebra. Analog dazu heißt eine Menge
quasi-invariant, falls die symmetrische
Differenz der Menge mit ihrem Urbild bezüglich des Wahrscheinlichkeitsmaßes
eine Nullmenge bildet, also wenn
gilt
.
Definition
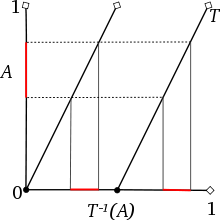
Eine maßerhaltende Transformation heißt nun ergodisch, falls für alle
T-invarianten Mengen A gilt, dass .
Die Mengen bilden also eine P-triviale
σ-Algebra. Das 4-Tupel
bestehend aus Wahrscheinlichkeitsraum
und ergodischer maßerhaltender Abbildung
heißt dementsprechend ergodisches dynamisches System.
Neben dieser Definition gibt es eine Reihe äquivalenter Charakterisierungen.
Falls
ein maßerhaltendes dynamisches System ist,
dann sind folgende Aussagen äquivalent:
ist ergodisches maßerhaltendes System.
- Für jede quasi-invariante Menge
gilt entweder
oder
.
- Jede
-messbare Funktion
ist
-fast sicher konstant.
- Für alle
gilt:
.
Anwendungen
Mathematisch gesehen stellt der Birkhoffsche Ergodensatz für ergodische Maßtransformationen eine Variante des Starken Gesetzes der großen Zahlen dar. Dabei können durchaus auch abhängige Zufallsvariablen betrachtet werden. Dasselbe gilt für den Lp-Ergodensatz.
Beispiele ergodischer Abbildungen
Rotation auf dem Einheitskreis
Betrachte das System
bestehend aus der Menge
,
der Borel-σ-Algebra
,
dem Lebesguemaß
und der Abbildung
.
Dieses System ist für alle
maßerhaltend. Es ist zudem genau dann ergodisch, wenn
nicht rational ist, sprich wenn gilt
.
Bernoulli-Shift
Auch beim Bernoulli-Shift
handelt es sich um eine ergodische Abbildung: Betrachte den Grundraum der -
-Folgen
mit zugehöriger Produkt-σ-Algebra
und zugehörigem unendlichen Produktmaß
definiert durch
.
Bei der Bernoulli-Abbildung
handelt es sich um dem Linksshift auf dem Grundraum
,
das heißt
ist definiert als
Dann ist das 4-Tupel
ein ergodisches dynamisches System.
Gauß-Abbildung
Sei der Grundraum
und
die entsprechende Borelsche
σ-Algebra. Definiere die Gauß-Abbildung
durch
Falls nun als Maß das Gaußmaß
,
,
gewählt wird, so handelt es sich bei
um ein ergodisches dynamisches System.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 22.02. 2021