Maßerhaltende Abbildung

Maßerhaltende Abbildungen, manchmal auch maßtreue Abbildungen genannt, sind Selbstabbildungen eines Wahrscheinlichkeitsraums, die das Wahrscheinlichkeitsmaß erhalten. Man spricht auch von maßerhaltenden dynamischen Systemen, insbesondere wenn man das Verhalten der Abbildung unter Iteration betrachtet.

Maßerhaltende Abbildungen sind das Thema der Ergodentheorie innerhalb der Theorie der dynamischen Systeme.

Definition

Sei $(X,\Sigma,P)$ ein Wahrscheinlichkeitsraum, d.h., sei eine Menge, $\Sigma\subset \mathcal P(X)$ die σ-Algebra der messbaren Mengen und ein Wahrscheinlichkeitsmaß. Eine messbare Abbildung

T : [0,1) → [0,1), $x \mapsto 2x \mod 1$ ist eine maßerhaltende Abbildung für das Lebesgue-Maß auf [0,1].

$f\colon X\to X$

heißt maßerhaltende Abbildung, wenn für alle $A\in\Sigma$

$P(f^{-1}(A))=P(A)$

gilt.

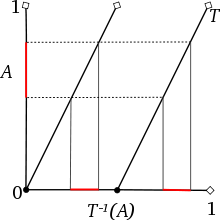
Man beachte, dass für eine maßerhaltende Abbildung nicht notwendig P(f(B))=P(B) für die messbaren Mengen gelten muss, dass also nur Urbilder und nicht unbedingt Bilder messbarer Mengen dasselbe Maß haben. Das Bild rechts zeigt die Bernoulli-Abbildung (Winkelverdopplung) $T(x)=2x \mod 1$ . Diese Abbildung ist maßerhaltend, zum Beispiel gilt für jedes Intervall $T^{-1}(a,b)=(\frac{a}{2},\frac{b}{2})\cup(\frac{a+1}{2},\frac{b+1}{2})$ , also

$P(T^{-1}(a,b))=\frac{b-a}{2}+\frac{b-a}{2}=b-a=P(a,b)$ .

Trotzdem müssen Bildmengen nicht dasselbe Maß wie die Ursprungsmenge haben, zum Beispiel ist $P(0,\frac{1}{2})=0{,}5$ , aber $P(T(0,\frac{1}{2}))=P(0,1)=1$ .

Beispiele

Maßerhaltende Abbildungen

sei der Einheitskreis, $\Sigma$ die σ-Algebra der Borelmengen und das gleichverteilte Wahrscheinlichkeitsmaß $\frac{1}{2\pi}d\theta$ . Jede Drehung des Einheitskreises ist eine maßerhaltende Abbildung.
Die durch eine ganzzahlige unimodulare Matrix $A\in GL(n,\Z)$ definierte Selbstabbildung $f\colon T^n\to T^n$ des n-dimensionalen Torus $T^n=\R^n/\Z^n$ gegebene Abbildung ist maßerhaltend bzgl. des Wahrscheinlichkeitsmaßes $\frac{1}{(2\pi)^n}d\theta_1\ldots d\theta_n$ .
Eine Intervall-Austausch-Abbildung ist maßerhaltend.

Maßerhaltende dynamische Systeme

Eine wichtige Klasse von maßerhaltenden dynamischen Systemen bilden die stationären stochastischen Prozesse in diskreter Zeit. Dazu definiert man einen kanonischen Prozess $(\Omega, \mathcal A, P)= (E^{\times \N}, \mathcal B (E)^{\otimes E},P)$ und den Shift-Operator $\tau$ als

$\tau ((\omega _{n})_{n\in \mathbb {N} })=(\omega _{n+1})_{n\in \mathbb {N} }$ .

Dann ist $X_n(\omega)=X_0(\tau^n(\omega))$ und $(\Omega, \mathcal A, P, \tau)$ ist ein dynamisches System, das aufgrund der Stationarität maßerhaltend ist.

Invarianten

Eine die Chaotizität maßerhaltender Abbildungen messende Invariante ist die Kolmogorow-Sinai-Entropie.

Literatur

Peter Walters: Ergodic theory—introductory lectures (= Lecture Notes in Mathematics. Vol. 458). Springer, Berlin/New York, 1975.
James R. Brown: Ergodic theory and topological dynamics (= Pure and Applied Mathematics. 70). Academic Press [Harcourt Brace Jovanovich, Publishers], New York/London, 1976.
H. Furstenberg: Recurrence in ergodic theory and combinatorial number theory. (= M. B. Porter Lectures). Princeton University Press, Princeton, N.J., 1981, ISBN 0-691-08269-3.
Daniel J. Rudolph: Fundamentals of measurable dynamics. Ergodic theory on Lebesgue spaces. Oxford Science Publications. The Clarendon Press, Oxford University Press, New York, 1990, ISBN 0-19-853572-4.

Basierend auf einem Artikel in:

Wikipedia.de