Anomale Diffusion

Mittlere quadratische Verschiebung $\langle r^2(\tau)\rangle$ für normale, Super- und Subdiffusion

Anomale Diffusion ist in der statistischen Physik eine besondere Art des Transportprozesses Diffusion bzw. der brownschen Molekularbewegung, die in vielen komplexen (z.B. viskoelastischen) Medien auftritt. Sie lässt sich nicht durch das gewöhnliche (Fick’sche) Diffusionsgesetz beschreiben. Im Unterschied zu normaler Diffusion wächst die mittlere quadratische Verschiebung $\langle r^2(\tau)\rangle$ eines anomal diffundierenden Teilchens, also der Raum, den das Teilchen in der Zeit $\tau$ durchwandert, nicht proportional zu $\tau$ , sondern folgt typischerweise einem Potenzgesetz $\langle r^{2}(\tau )\rangle \propto \tau ^{\alpha }$ mit Anomalieparameter α. Anomale Diffusion beschreibt Zufallsbewegungen mit lang-reichweitigen Korrelationen, für die der zentrale Grenzwertsatz der Statistik nicht mehr gilt. Solche Transportprozesse treten zum Beispiel in Zellen oder beim Reiseverhalten von Menschen auf.

Definition und Eigenschaften

Definition

Übliche Diffusionsprozesse lassen sich makroskopisch durch die Fick’sche Diffusionsgleichung beschreiben. Mikroskopisch geht diese Beschreibung in eine Brown’sche Molekularbewegung (Wiener-Prozess) über, mit der mittleren quadratische Verschiebung:

$\langle \Delta r^{2}(\tau )\rangle _{\text{normale Diffusion}}=2n\cdot D\cdot \tau$

Der Faktor gibt die Zahl der Raumdimensionen an und der Parameter D ist der Diffusionskoeffizient.

Anomale Diffusion zeichnet sich dagegen durch folgende Abhängigkeit aus:

$\langle \Delta r^{2}(\tau )\rangle _{\text{anomale Diffusion}}=2n\cdot K_{\alpha }\cdot \tau ^{\alpha },\quad \alpha >0$

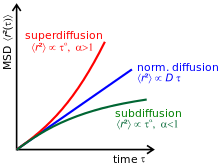
Hier ist $K_{{\alpha }}$ ein verallgemeinerter Diffusionskoeffizient und $\alpha$ der Anomalieparameter. Die Einheit dieses verallgemeinerten Diffusionskoeffizienten ist $[K_{\alpha }]=m^{2}/s^{\alpha }$ , hängt also vom Anomalieparameter ab. Man unterscheidet zwei Regime, die auch in der Abbildung ganz oben dargestellt sind:

Subdiffusion ( $0<\alpha <1$ ): Diese Art der verlangsamten diffusiven Bewegung kann etwa im Inneren von Zellen und bei Random Walks auf fraktalen Strukturen beobachtet werden.
Der Spezialfall $\alpha =1$ beschreibt die gewöhnliche normale Diffusion.
Superdiffusion ( $\alpha >1$ ): Diese beschleunigte Diffusion tritt z.B. bei Lévy-Flügen auf, oder etwa bei der Bewegung von Geldscheinen bzw. Reisebewegung von Menschen.
Der Spezialfall $\alpha =2$ wird ballistische Diffusion (englisch ballistic diffusion) genannt. Dies entspricht einem Fall, wo zusätzlich zur Diffusionsbewegung auch eine Drift vorliegt.

Anomale Diffusion als makroskopischer Effekt

Anomale Diffusion an sich ist zunächst ein makroskopischer Effekt. Wie die verschiedenen obigen Beispiele schon zeigen, ist das Herleiten der mikroskopischen Ursache der anomalen Diffusion nicht einfach möglich.

Zeitabhängiger Diffusionskoeffizient und Gedächtnis

Die mittlere quadratische Verschiebung lässt sich formal auch durch einen zeitabhängigen Diffusionskoeffizienten $D_{\alpha }(\tau )$ ausdrücken:

$\langle \Delta r^{2}(\tau )\rangle _{\text{anomale Diffusion}}=2n\cdot D_{\alpha }(\tau )\cdot \tau \quad {\text{mit}}\quad D_{\alpha }(\tau )=K_{\alpha }\cdot \tau ^{\alpha -1}$

Der Diffusionskoeffizient ist also nicht mehr zeitlich konstant, das Verhalten (die "Diffusionsgeschwindigkeit") eines Teilchens hängt also davon ab, wie lange es sich schon bewegt (für Subdiffusion wird es z.B. immer langsamer, je länger es sich bewegt). Dies bedeutet, dass quasi ein Gedächtnis im System vorhanden ist, das die aktuelle Bewegung von der Vorgeschichte abhängig macht. Ein detaillierteres mathematisches Modell hierfür wird weiter unten im Abschnitt Anomale Diffusion und die Langevin-Gleichung beschrieben.

Auftreten anomaler Diffusion

Anomale Diffusionsphänomene treten in verschiedenen Systemen auf. Hier sollen einige Beispiele zusammengefasst werden, die teilweise im restlichen Artikel näher erläutert werden:

Superdiffusion mit :
- im theoretischen Random-Walk-Modell des Lévy-Fluges
- bei der Bewegung von Geldscheinen bzw. Reisebewegung von Menschen. Reisende Menschen verbleiben z.B. typischerweise einige Zeit in einer Stadt und bewegen sich dort auf kleiner räumlicher Skala. Mit einer gewissen (niedrigen, aber nicht verschwindenden) Wahrscheinlichkeit unternehmen sie dann eine Reise in eine entfernte Stadt, was zu einem großen Sprung führt. Lévy-Flüge sind ein theoretisches Modell für solches Verhalten.
- Bewegung einzelner Zellen in Zellaggregaten

Subdiffusion mit :
- Im Inneren von Zellen beobachtet man Subdiffusion bei der Bewegung von Makromolekülen durch das Cytoplasma. Eine Ursache hierfür kann das sog. molecular crowding sein, also das Vorhandensein vieler (dicht gepackter) Makromoleküle und Organellen im Zytoplasma
- Auf Membranen von Zellen wird ebenfalls anomale Diffusion beobachtet. Die Zellmembran ist hier ein komplexes System aus vielen verschiedenen Bausteinen (Flüssig-Mosaik-Modell).
- Random Walks auf fraktalen Strukturen, wie etwa Perkolationsklustern. Dies kann auch experimentell durch NMR-Diffusivitätsmessungen in porösen Systemen gezeigt werden.
- Diffusion in Polymernetzwerken
- Die Monomerbewegung von langen Polymeren wie DNA zeigt auf begrenzten Zeitskalen ebenfalls die Charakteristik anomaler Diffusion, hier ausgelöst durch die eingeschränkte interne Bewegung des Polymers (siehe z.B. das einfache Rouse-Modell für die Polymerdynamik).
- Ladungsträgertransport in amorphen Halbleitern

Theoretische Beschreibung durch Random Walks

Normale Diffusion

1000 Schritte eines normal-diffusiven (α = 1) Random-Walk

Wie schon erwähnt, zeigen gewisse Random Walk-Prozesse ein anomal diffusives Verhalten. Dabei beschreibt man das Fortschreiten der (hier im Beispiel eindimensionalen) Bewegung in diskreten Zeitschritten $\Delta t$ . Der Positionssprung $\Delta x=x_{t}-x_{t-1}$ von einem Zeitschritt zum nächsten ist für normale Diffusion gauß-verteilt:

$p(\Delta x)\propto \exp \left(-{\frac {1}{2}}\cdot {\frac {\Delta x^{2}}{2D\cdot \Delta t}}\right)$

Diese charakteristische Gauß-Verteilung gilt aufgrund des zentralen Grenzwertsatzes der Statistik für viele Vorgänge. Sind allerdings wie in den folgenden Beispielen seine Voraussetzungen nicht mehr erfüllt (z.B. weil die Varianz (Stochastik) $\sigma ^{2}=2D\cdot \Delta t$ der obigen Verteilung nicht mehr definiert werden kann), so kann man anomal diffusives Verhalten beobachten.

Lévy-Flüge

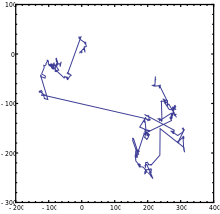
Ein Lévy-Flug mit seiner erhöhten Wahrscheinlichkeit von langen Sprüngen zeigt Superdiffusion (α > 1). Das Bild zeigt ebenfalls 1000 Schritte und man kann deutlich die seltenen langen Sprünge erkennen.

Anomale Superdiffusion tritt in Random Walk-Prozessen auf, bei denen die Sprunglängenverteilung endlastig ist. Hier gilt der zentrale Grenzwertsatz nicht mehr, da die Varianz von endlastigen Verteilungen divergiert. Ein Beispiel sind die bereits erwähnten Lévy-Flüge, bei denen selten (aber häufiger als in einer Gauß-Verteilung) sehr lange Sprünge vorkommen können. Die Sprunglängenverteilung nimmt hier mit einem Potenzgesetz ab:

$p(\Delta x)\propto |\Delta x|^{-(1+2/\alpha )},\alpha >1,\ \ \ {\text{für}}\ \ \ \Delta x\rightarrow \infty$

Im Bild rechts sind einige Schritte eines solchen Prozesses gezeigt. Die seltenen großen Sprünge sind gut zu erkennen.

Continuous time random walks (CTRW)

Ein weiterer Random Walk-Prozess mit anomal diffusiver Charakteristik sind sog. Continuous time random walks (CTRW). Dabei ist die Bewegung nicht in gleich lange Zeitschritte $\Delta t$ zerteilt, sondern bei gleich bleibender Sprunglänge $\Delta x$ wird die Wartezeit zwischen zwei Sprüngen aus einer Verteilung betrachtet. Man kann das auch als Diffusion auf einem Gitter mit Fallen auffassen, wobei die Fallen das diffundierende Teilchen unterschiedlich lange festhalten können. Ist die Wartezeitverteilung endlastig, also:

$p(\Delta t)\propto \Delta t^{-(1+\alpha )},0<\alpha <1,\ \ \ {\text{für}}\ \ \ \Delta t\rightarrow \infty$

so führt auch dieses zu anomaler Subdiffusion mit Anomalieparameter $\alpha$ .

Kontinuierliche theoretische Modelle

Anomale Diffusion und die Langevin-Gleichung

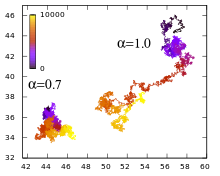
Normale (α=1) und subdiffusive (α=0.7) Bewegung eines Teilchens. Für eine detaillierte Beschreibung des Algorithmus zur Berechnung des Bildes siehe Ref. Das Fortschreiten der Zeit (10000 Schritte) ist als Farbe codiert (siehe Farbbalken links oben)

Normal diffundierende Teilchen in einem viskosen Medium können über die Langevin-Gleichung beschrieben werden:

$m\cdot {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-\xi \cdot {\frac {\mathrm {d} x}{\mathrm {d} t}}+F_{\text{st}}(t)$

Dabei ist x(t) der Teilchenort zur Zeit t, ξ der Reibungskoeffizient und F_st eine stochastische Kraft mit verschwindender Korrelation $\langle F(t)\cdot F(t')\rangle \propto \delta (t-t')$ , also weißes Rauschen. Diese stochastische Differentialgleichung lässt sich zur fraktionalen Langevin-Gleichung verallgemeinern:

$m\cdot {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-\xi \cdot \int \limits _{-\infty }^{t}K(t-t'){\frac {\mathrm {d} x(t')}{\mathrm {d} t}}\;\mathrm {d} t+F_{\text{st}}(t)$

Dabei ist nun $K(\tau)$ ein sog. memory kernel (deutsch etwa Gedächtnis-Faltungskern), der eine (auch langreichweitige) zeitliche Kopplung induziert. Die Bewegung des Teilchens hängt also auch von seiner Vergangenheit (Integral $\int _{-\infty }^{t}...$ ) ab, was bei normaler Brownscher Bewegung nicht der Fall war (dies entspricht einem nicht-markovschen Random-Walk). Nimmt man nun im Speziellen wieder ein Potenzgesetz für $K(\tau)$ an, also

$K(\tau )\propto \tau ^{-\alpha }$

so folgt auch aus diesem Ansatz eine anomale mittlere quadratische Verschiebung mit Anomalie α. Mit diesem Ansatz kann man anomale Diffusion modellieren, wie sie in viskoelastischen Medien auftritt. Alternativ kann man den stochastischen Term korrelieren lassen, etwa $\langle F(t)\cdot F(t')\rangle \propto \exp(-|t-t'|)$ . Dies entspricht einer Diffusion mit Hindernissen, die für Zeitskalen, in der einerseits die Hindernisgröße und andererseits der mittlere Hindernisabstand nicht verschwindet gegenüber diffundierten Distanzen, auch eine anomale Subdiffusion ist.

Fraktionale Diffusionsgleichung

Mit Hilfe der in der Fraktionale Infinitesimalrechnung definierten fraktionalen Integro-Differential-Operatoren lässt sich die oft zur Modellierung normaler Diffusionsphänomene herangezogene Fokker-Planck-Gleichung auf anomale Diffusion erweitern. Diese (dann fraktionale) Differentialgleichung beschreibt die Zeitentwicklung der Aufenthaltswahrscheinlichkeit $W(x,t)$ diffundierender Teilchen am Ort zur Zeit .

${\frac {\partial W(x,t)}{\partial t}}=K_{\alpha }\cdot \mathbb {D} _{t}^{1-\alpha }{\frac {\partial ^{2}W(x,t)}{\partial x^{2}}}$

Dabei ist der Riemann-Liouville-Operator $\mathbb {D} _{t}^{1-\alpha }f(t)$ anschaulich als die $\alpha$ -te Ableitung der Funktion f(t) nach der Zeit definiert über die Integraldarstellung:

$\mathbb {D} _{t}^{1-\alpha }f(t)={\frac {1}{\Gamma (\alpha )}}{\frac {\partial }{\partial t}}\int \limits _{0}^{t}{\frac {f(t')}{(t-t')^{1-\alpha }}}\;\mathrm {d} t'$

Dabei ist $\Gamma (x)$ die Gamma-Funktion. Die Lösung dieser fraktionalen Differentialgleichung führt wieder auf die anomale mittlere quadratische Verschiebung:

$\langle r^{2}(\tau )\rangle ={\frac {2K}{\Gamma (1+\alpha )}}\cdot \tau ^{\alpha }$

Literatur

Ralf Metzler, Joseph Klafter: The random walk's guide to anomalous diffusion: a fractional dynamics approach. In: Physics Reports. 339, Nr. 1, Dezember 2000, S. 1–77. doi:10.1016/S0370-1573(00)00070-3.
Rainer Klages, Günter Radons, Igor M. Sokolov (Herausgeber) Anomalous Transport, John Wiley & Sons, 2008, ISBN 978-3-527-40722-4

Basierend auf einem Artikel in:

Wikipedia.de