Mittlere quadratische Verschiebung
Die mittlere quadratische Verschiebung (oft als englisch mean squared
displacement, MSD, bezeichnet und mit dem Symbol
bezeichnet, Definition siehe unten) ist in der statistischen
Physik ein Maß für die Strecke, die ein Teilchen im Mittel (z.B. über
viele Versuche) in einer gewissen Zeit zurücklegt. Dieses Maß ist besonders bei
der Beschreibung Brownscher
Dynamik und anderen Zufallsbewegungen wichtig, da dort typischerweise keine
ausgezeichnete Richtung vorliegt, entlang der man eine zurückgelegte Strecke
messen könnte.
Anschauliche Beschreibung und Interpretation
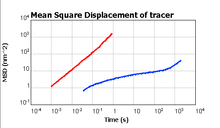
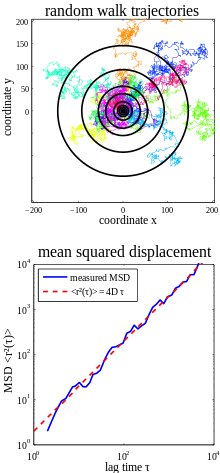
Anschaulich ist die mittlere quadratische Verschiebung ein Maß für das Volumen, das ein Teilchen, das eine Zufallsbewegung ausführt, in einer gewissen Zeit durchstreift. Als Beispiel betrachtet man eine reine Brownsche Bewegung in zwei Dimensionen (vgl. Abbildung rechts). Lässt man mehrere Teilchen (in der Abbildung oben in verschiedenen Farben) am gleichen Ort starten, so bewegen sich zwar einzelne Teilchen vom Startpunkt weg, aber jeweils in unterschiedliche Richtungen. Auch kann jedes Teilchen durchaus zum Startpunkt zurückkehren. Mittelt man nun über alle Teilchenpositionen nach einer Wartezeit τ, so wird dieser Mittelwert wieder nahe dem Startpunkt liegen, die Teilchen haben sich also im Mittel nicht fortbewegt. Hätten die Teilchen im Gegensatz dazu eine Vorzugsrichtung, so würde sich auch ihr Mittelwert mit einer gewissen Geschwindigkeit in diese Vorzugsrichtung bewegen.
Man beobachtet aber nun, dass die Teilchen eine umso größere Fläche
überstreichen je länger man wartet (konzentrische Kreise in der Abbildung, die
äußeren Kreise entsprechen längeren Wartezeiten τ), das heißt je länger man
wartet, desto eher befindet sich auch einmal ein Teilchen in größerem Abstand
vom Ausgangspunkt. Zur Beschreibung dieser überstrichenen Fläche (die langsam
mit der Wartezeit τ wächst) kann man nun die mittlere quadratische Verschiebung
aller Teilchen nutzen: Ihre Wurzel
()
beschreibt nämlich den Radius dieser größer werdenden Kreise/Fläche.
Man kann also die Kurve
so interpretieren, dass Teilchen, die sich nach ihr bewegen, nach einer Zeit τ
mit hoher Wahrscheinlichkeit schon einmal im Abstand
von ihrem Ausgangspunkt anzutreffen waren.
Exakte Definition
Die mittlere quadratische Verschiebung wird über den Ensemblemittelwert
über viele
Trajektorien
definiert:
Hierbei wird über viele Teilchen gemittelt, die jeweils über die Zeitspanne
beobachtet werden. Alternativ (und vor Allem in theoretischen Betrachtungen, in
denen diese Größen berechenbar sind) kann dies auch über die
Aufenthaltswahrscheinlichkeit (siehe Greensfunktion)
von Teilchen zur Zeit
geschrieben werden:
Man beachte, dass
den Abstand zum Startpunkt der Trajektorie (der in den Ursprung gelegt wird)
misst.
Je nach System kann die mittlere quadratische Verschiebung auch über einen Zeitmittelwert über eine
Trajektorie
eines Teilchens im Raum definiert werden:
Das bedeutet, dass nur ein Teilchen beobachtet wird, und dann ausgehend von
verschiedenen Zeitpunkten
gemessen wird, wie weit sich das Teilchen bis zur Zeit
bewegt hat. Es wird dann über die Verschiebungen
während aller möglichen Zeitspannen
innerhalb der Dauer
der Trajektorie gemittelt.
Beide Definitionen ergeben nur dann dieselbe Größe, wenn das betrachtete System ergodisch ist (siehe auch Ergodenhypothese). Oft werden auch Mischformen dieser zwei idealen Definitionen verwendet, besonders wenn in Experimenten beide Mittelwerte vermischt werden (z.B. bei der Fluoreszenz-Korrelations-Spektroskopie).
Zusätzlich wird oft auch die Wurzel aus der mittleren quadratischen Verschiebung
verwendet und dann meist als englisch root mean squared displacement (RMSD) bezeichnet.
Bedeutung
Besonders bei ungerichteten und zufälligen Bewegungen gibt es oft keine
ausgezeichnete Raumrichtung. Die Mittelung über die (vektoriellen)
Verschiebungen um den Anfangspunkt ist daher Null, da für jede Bewegung in eine
Richtung eine Bewegung in entgegengesetzte Richtung mit gleicher statistischer
Häufigkeit existiert. So ist beispielsweise die mittlere Auslenkung
eines Random Walks eines
einzelnen Teilchens für alle Zeiten
gleich Null. Trotzdem überdeckt das Teilchen in einer gegebenen Zeit einen
gewissen Raumbereich, der durch die mittlere quadratische Verschiebung
charakterisiert wird.
Für normale Diffusion ergibt sich ein einfacher Zusammenhang für die mittlere quadratische Verschiebung:
wobei
der Diffusionskoeffizient
und
die Anzahl der Raumdimensionen,
in denen die Bewegung stattfindet.
Für normale Diffusion
in Verbindung mit einer gerichteten Bewegung (Fluss der Geschwindigkeit )
ergibt sich weiter:
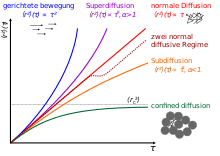
Im Falle anomaler Diffusion ergibt sich oft allgemeiner der Zusammenhang:
wobei
eine allgemeine Proportionalitätskonstante (verallgemeinerter
Diffusionskoeffizient, hängt u.U. von
ab!) ist und
die Anomalie der Bewegung beschreibt. Für
spricht man von Subdiffusion
und für
von Superdiffusion.
Für den Fall
ergibt sich wieder normale Diffusion.
Oft erfolgt die Diffusion in porösen
Medien, wobei nur ein Anteil des gesamten Volumens für die Teilchen
zugänglich ist. In solchen Systemen sieht man oft einen Übergang zwischen zwei
normal-diffusiven Regimen: Zunächst erfolgt schnelle Diffusion innerhalb einer
Pore. Auf längeren Zeitskalen geht das MSD dann in ein langsameres aber immer
noch normal diffusives Regime über, das die Diffusion zwischen den Poren
beschreibt.
Wird der Anteil des nicht zugänglichen Volumens so groß, dass die Poren nicht
mehr unbedingt verbunden sind, so sind die Teilchen in den entstehenden
abgegrenzten Raumbereichen gefangen. Man spricht von "confined
diffusion". Das MSD geht dann für große Zeitskalen gegen einen konstanten
Wert ,
der die Größe des zugänglichen Bereichs beschreibt. Das MSD kann dann
folgendermaßen modelliert werden (mit freien Fit-Parametern
):
In vielen Systemen beschränkt sich die Anomalie einer Bewegung auf einen
bestimmten Zeitbereich für .
Oberhalb dieser kritischen Zeit
geht die Bewegung wieder in normale Diffusion über. Dieser Fall ist z.B.
in der Kurve für viskoelastische Flüssigkeiten zu sehen und tritt z.B.
auch bei der Monomerdynamik von Polymeren
auf.
Messung und Anwendung
Die mittlere quadratische Verschiebung wird oft zur Charakterisierung von zufälligen Bewegungen in Simulationen benutzt. Dabei kann sie direkt aus den simulierten Teilchentrajektorien bestimmt werden. Mit Hilfe des Zusammenhangs für normale Diffusion (*) kann etwa ein Diffusionskoeffizient D aufgrund der Gitterweite a und des Zeitschritts Δt der Simulation definiert werden:
Damit kann dann die Simulation, die oft in idealisierten und normalisierten Koordinaten abläuft, auf reale Systeme normiert werden.
Die mittlere quadratische Verschiebung ist auch experimentell zugänglich. So kann sie etwa durch Single-Particle-Tracking-Techniken direkt aus den dort gemessenen Trajektorien bestimmt werden. Auch mit Hilfe von Fluoreszenz-Korrelations-Spektroskopie ist sie unter gewissen Annahmen experimentell zugänglich. Es kann dann aus der gemessenen Kurve ⟨r²(τ)⟩ auch der Diffusionskoeffizient bestimmt werden:
Verbindung zur Geschwindigkeitsautokorrelation
Die mittlere quadratische Verschiebung steht über die Green-Kubo-Relation
in enger Verbindung zur Geschwindigkeitsautokorrelationsfunktion
:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.03. 2023